4장 - word2vec 속도 개선

CBOW 모델은 corpus에 포함된 어휘 수가 많아지면 계산량이 커지기 때문에 계산 시간이 오래 걸린다. 이번 장에서는 word2vec의 속도를 개선하기 위해 다음의 두 가지를 살펴본다.

• Embedding 계층
• Negative Sampling 손실 함수

4.1 - word2vec 개선 1

CBOW 모델로 거대한 corpus를 다룰 경우 다음과 같은 상황이 된다.

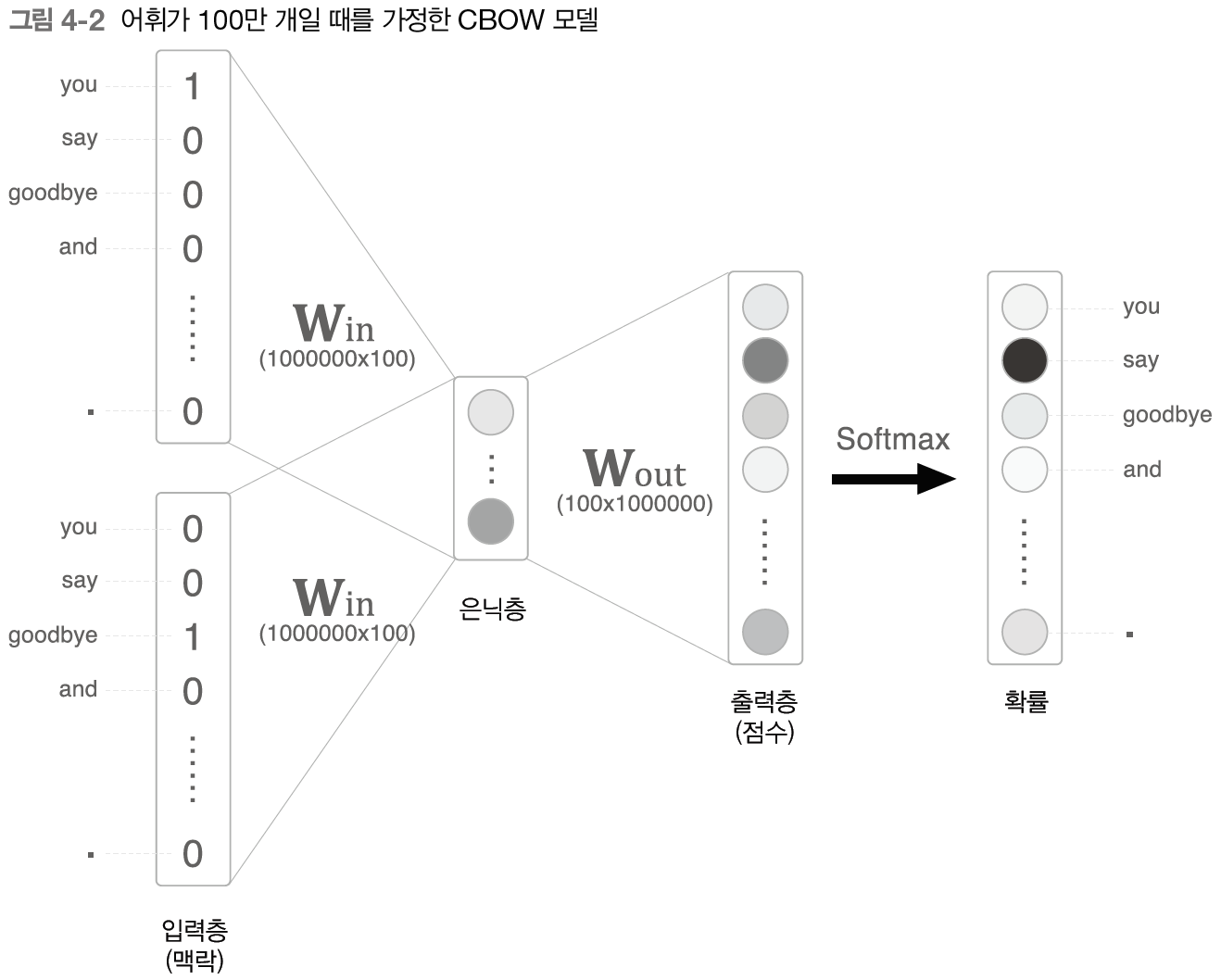
수많은 뉴런 때문에 중간 계산에 많은 시간이 소요된다. 정확히는 다음의 두 계산이 병목이 된다.

• 입력층의 원핫 벡터와 $\bold W_{in}$의 곱 계산
  -> Embedding 계층 도입으로 해결
• 은닉층과 가중치 행렬 $\bold W_{out}$의 곱 및 Softmax 계층의 계산
  -> 네거티브 샘플링 도입으로 해결

4.1.1 - Embedding 계층

단어의 원핫 표현과 가중치 행렬의 곱은 결과적으로 가중치 행렬의 특정 행을 추출하는 것과 같다.

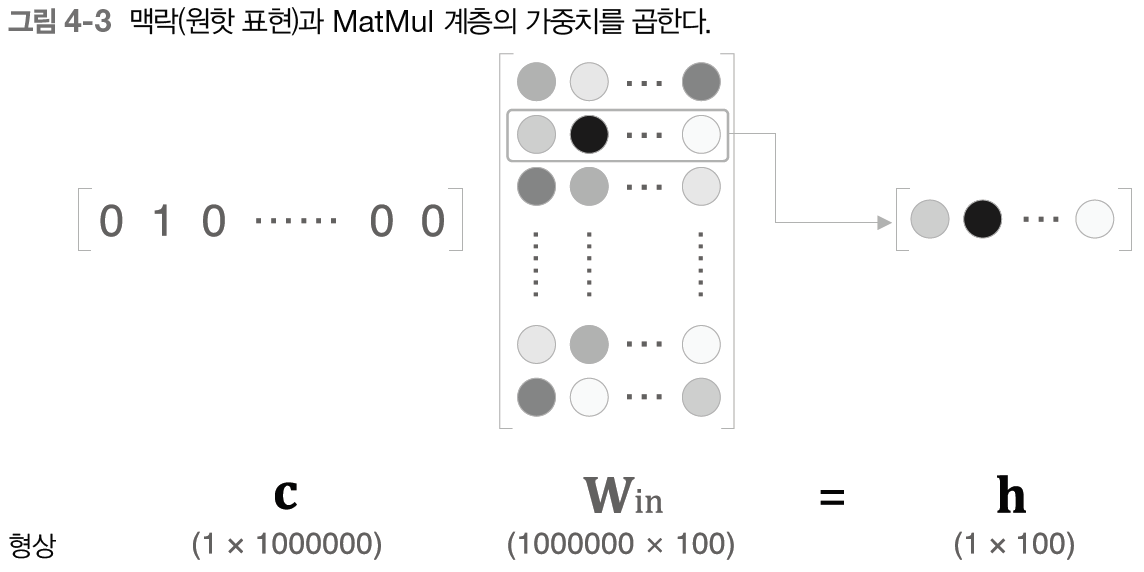
이 추출을 담당하는 계층을 Embedding 계층이라 한다. 굳이 행렬곱을 전부 하지 않고 추출하는 것으로 끝내는 것이다.

전에 말했던 분산 표현은 단어의 밀집벡터 표현을 의미한다. 다른 말로는 단어 임베딩이라고도 한다.

4.1.2 - Embedding 계층의 역전파

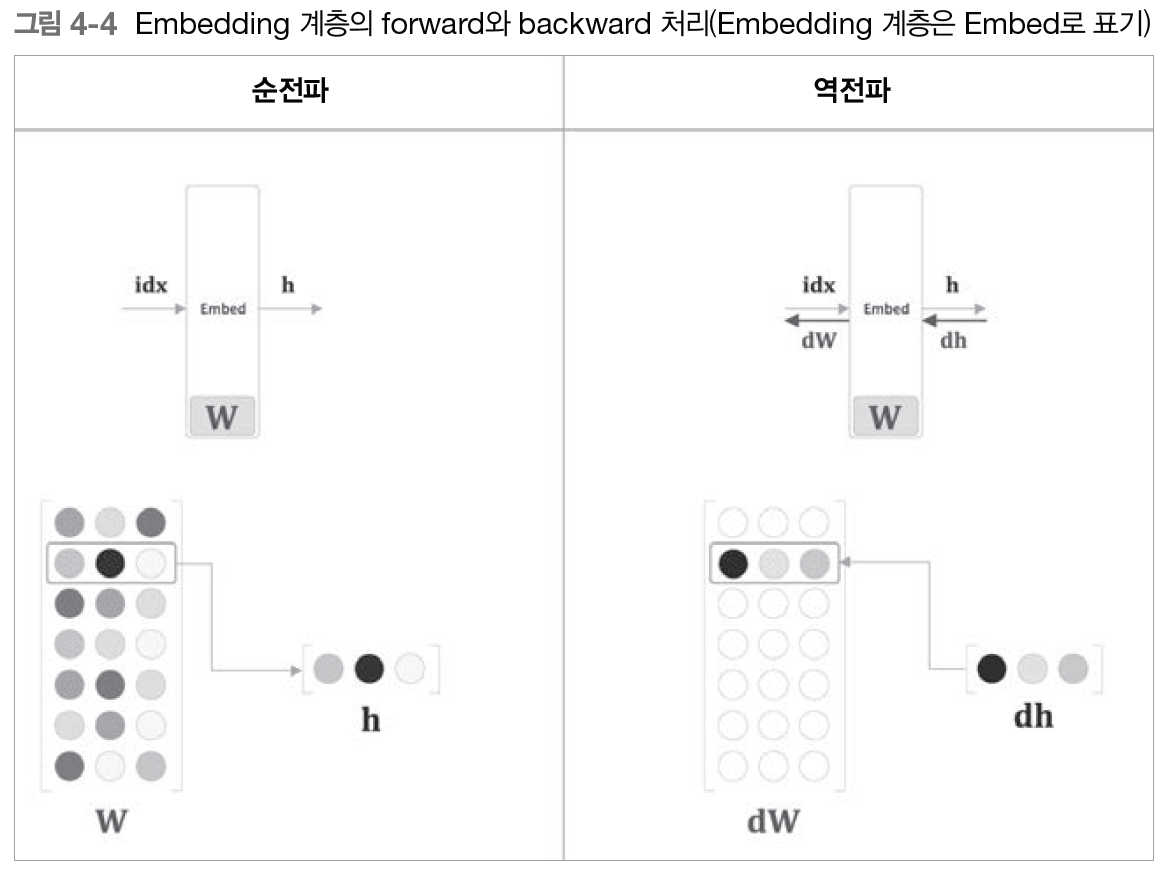
앞 층(출력 쪽 층)에서 전해진 기울기를 그대로 다음 층(입력 쪽 층)으로 흘려주면 된다. 다만, 순전파로 들어왔던 가중치 행렬의 인덱스를 유지해야 한다.

만약 "apple"이라는 단어의 인덱스가 2였다면, 역전파에서도 2의 인덱스에 "apple"에 대한 기울기 정보를 넣어줘야 한다.

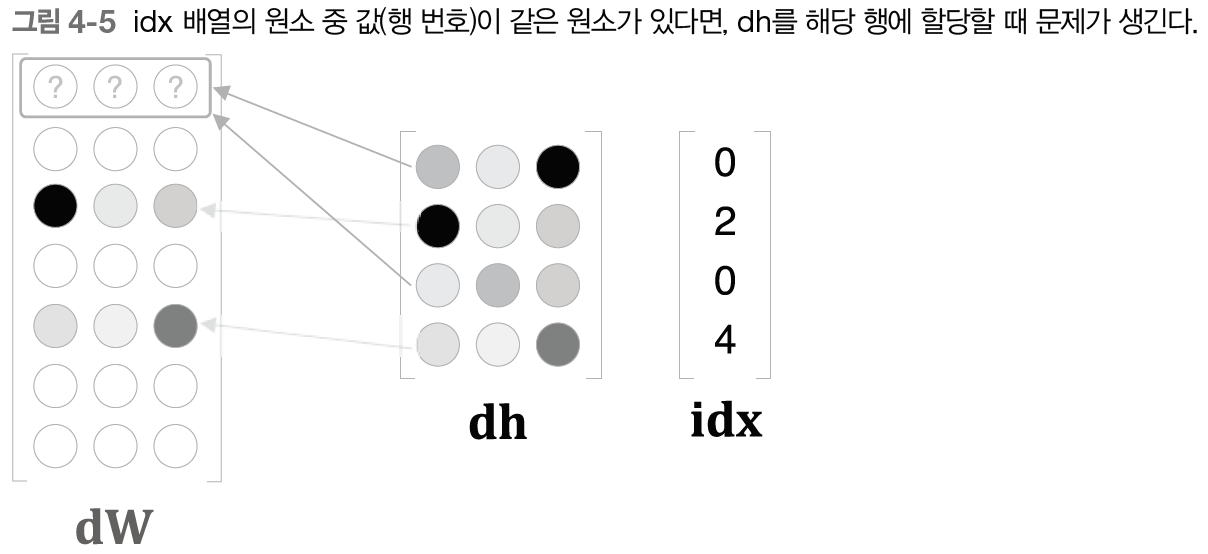
다만 해당 인덱스에 값을 덮어쓰는 게 아니라 더해줘야 한다는 점에 주의하자. 같은 단어가 여러 번 나오면 인덱스가 겹치기 때문이다.

4.2 - word2vec 개선 2

이번에는 네거티브 샘플링을 사용해서 은닉층 이후의 처리에서 생기는 병목을 해결해 보자. 네거티브 샘플링을 이용하면 어휘가 아무리 많아져도 계산량을 낮은 수준에서 일정하게 억제할 수 있다.

4.2.1 - 은닉층 이후 계산의 문제점

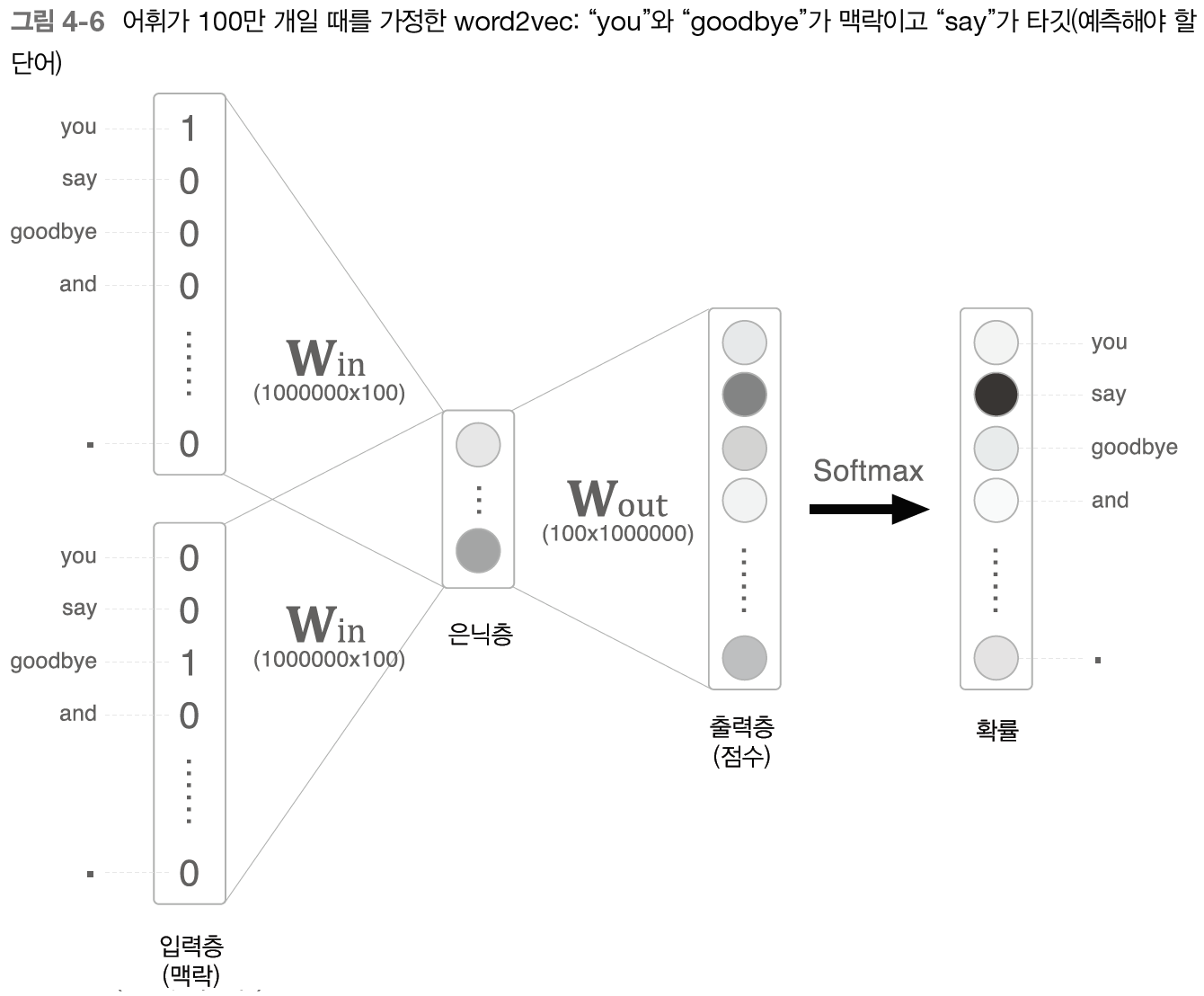
은닉층 이후에서 계산이 오래 걸리는 곳은 두 부분이다.

• 은닉층의 뉴런과 가중치 행렬($\bold W_{out}$)의 곱
• Softmax 계층의 계산

첫 번째는 거대한 행렬을 곱하는 문제이다. 행렬곱을 가볍게 만들 수 있다면 해결할 수 있다.

두 번째는 Softmax에서도 같은 문제가 발생한다는 것이다.

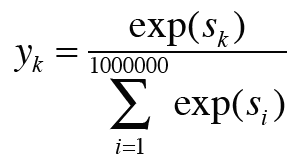
이 계산은 굉장히 무겁기 때문에 가벼운 계산이 필요해 보인다.

4.2.2 - 다중 분류에서 이진 분류로

네거티브 샘플링의 핵심 아이디어는 다중 클래스 분류를 이진 분류로 근사하는 데 있다.

다중 클래스 분류를 이진 분류로 근사하면 질문은 다음과 같은 식이 되겠다.

맥락이 'you'와 'goodbye'일 때 타깃 단어는 'say'인가?

이렇게 하면 출력층에는 "say"의 점수를 출력하는 뉴런 하나만 준비하면 된다.

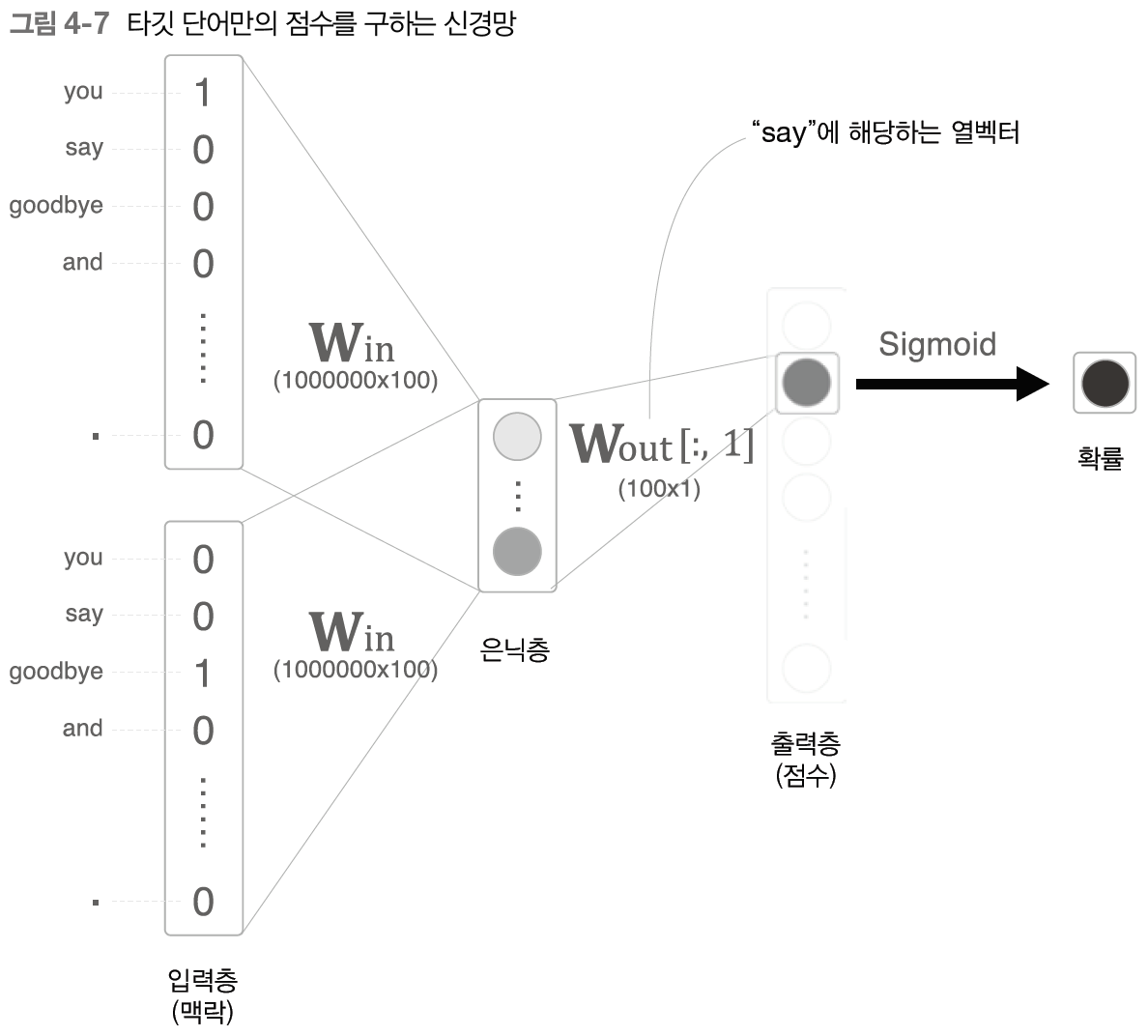
$\bold W_{out}$에서 "say"에 해당하는 열만 추출해서 내적을 계산하면 끝이다.

소프트맥스는 점수가 하나일 때는 의미가 없으므로 시그모이드를 사용해 확률을 구한다.
다중 클래스 분류에서는 소프트맥스를, 이진 분류에서는 시그모이드를 사용한다.

다음은 이 계산을 자세히 그린 것이다.

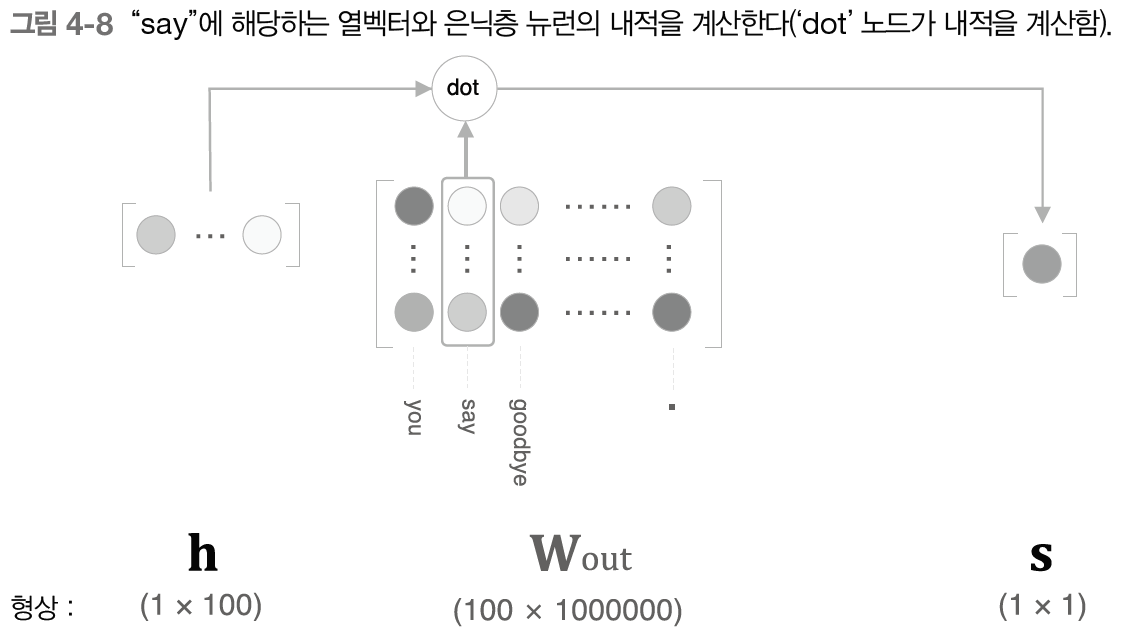
4.2.3 - 시그모이드 함수와 교차 엔트로피 오차

이진 분류 신경망에서는 점수를 시그모이드 함수를 적용해 확률로 변환하고 교차 엔트로피 오차를 손실 함수로 사용한다. 이 조합이 이진 분류 신경망에서 가장 흔하게 사용하는 조합이다.

시그모이드와 교차 엔트로피 오차의 식은 다음과 같다.

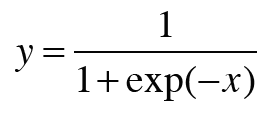
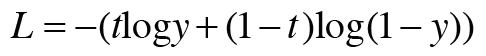
이어서 Sgmoid 계층과 Cross Entropy Error 계층의 계산 그래프를 살펴보자.

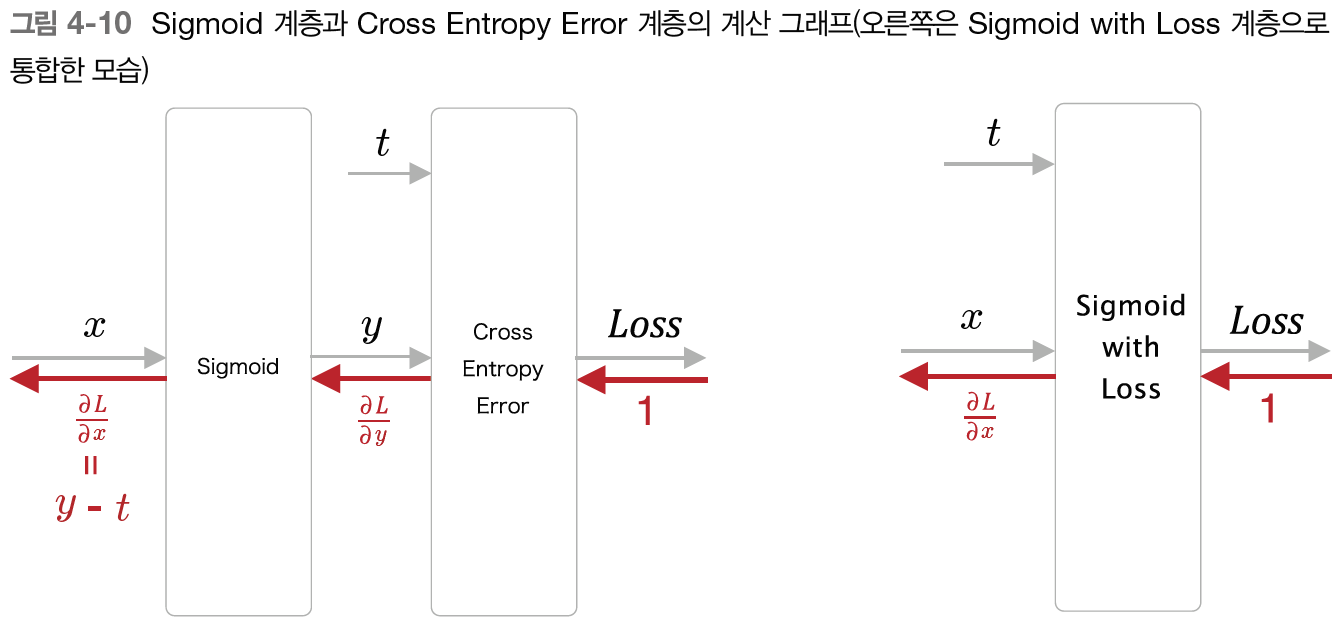
이전에 Softmax-with-Loss 계층을 설명할 때 역전파의 값이 $y-t$였다. 그런데 이번에도 같다.

유도 과정은 다음과 같다.

$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial x}\\ \frac{\partial L}{\partial y} =-\frac{t}{y}+\frac{1-t}{1-y}=\frac{y-t}{y(1-y)}\\ \frac{\partial y}{\partial x}=y(1-y)\\ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial x}=\frac{y-t}{y(1-y)}y(1-y)=y-t\\ \therefore \frac{\partial L}{\partial x}=y-t$

• 시그모이드 함수와 교차 엔트로피 오차
• 소프트맥스 함수와 교차 엔트로피 오차
• 항등 함수와 MSE(평균 제곱 오차)의 조합

위 조합들에서는 역전파의 값이 $y-t$로 깔끔하게 떨어진다.

4.2.4 - 다중 분류에서 이진 분류로 (그래프)

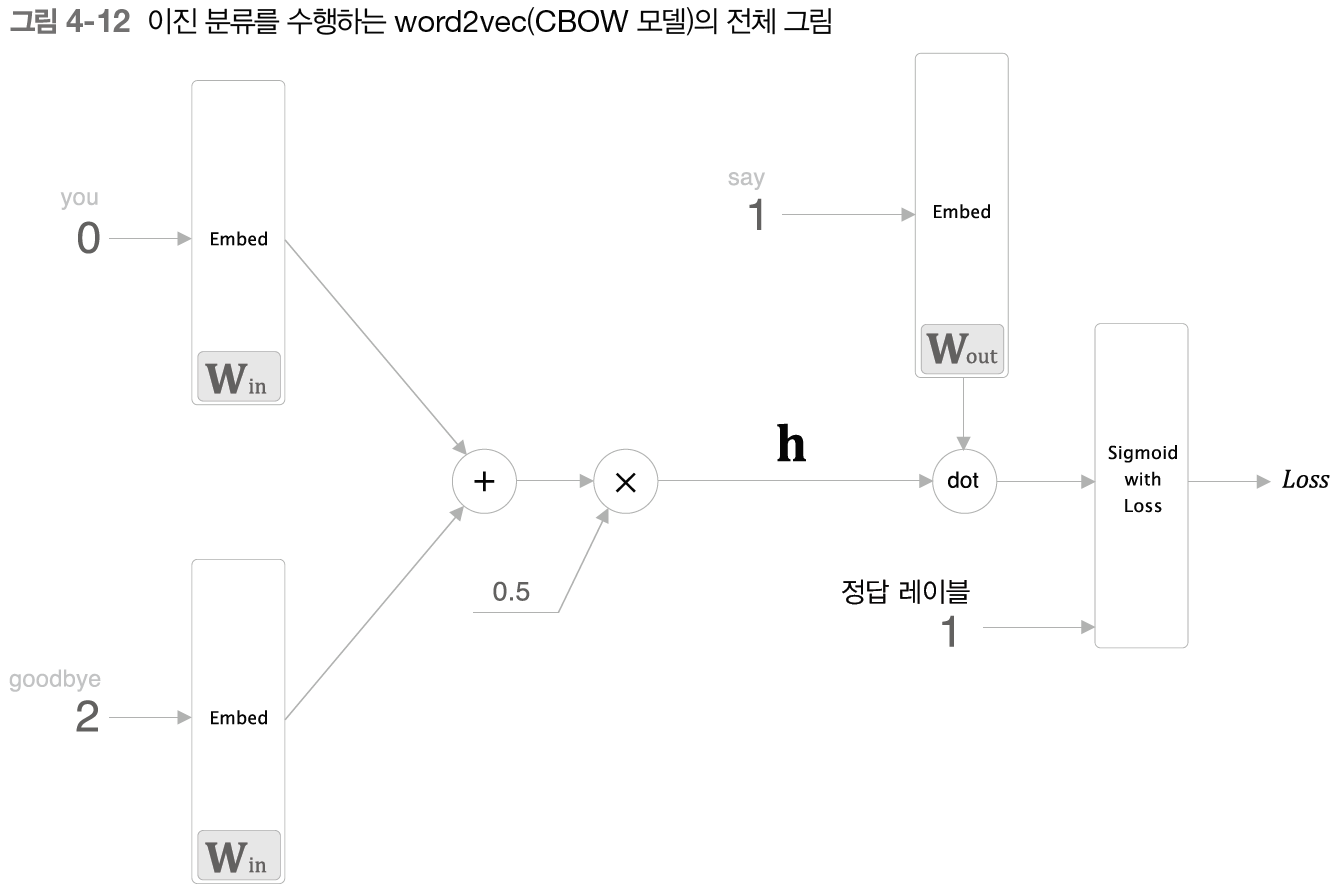
위에서 말했던 대로 "say"에 해당하는 열벡터만 Embedding 계층으로 추출하여 내적을 계산해 주면 된다.

4.2.5 - 네거티브 샘플링

지금까지 다중 분류를 이진 분류로 변환하는 것에 대해 배웠다. 그러나 이것으로 다 해결되지는 않는다. 지금까지는 긍정적인 예, 즉 정답에 대해서만 학습했기 때문이다.

우리가 원하는 것은 정답에 대해서는 1에 가까운 출력을, 오답에 대해서는 0에 가까운 출력을 내는 신경망이다. 그러기 위해 오답에 대해서도 학습이 필요하다.

하지만 여기서 생각해야 할 것이 있다. 바로 정답은 적지만 오답은 많다는 사실이다. 모든 어휘를 대상으로 하면 감히 상상할 수도 없는 수의 오답이 존재한다. 이 많은 오답을 학습시킬 수는 없다. 그래서 근사적인 해결법으로 부정적 예(오답)을 몇 개 샘플링해 사용하여 학습 시간을 줄인다. 이게 바로 네거티브 샘플링이다.

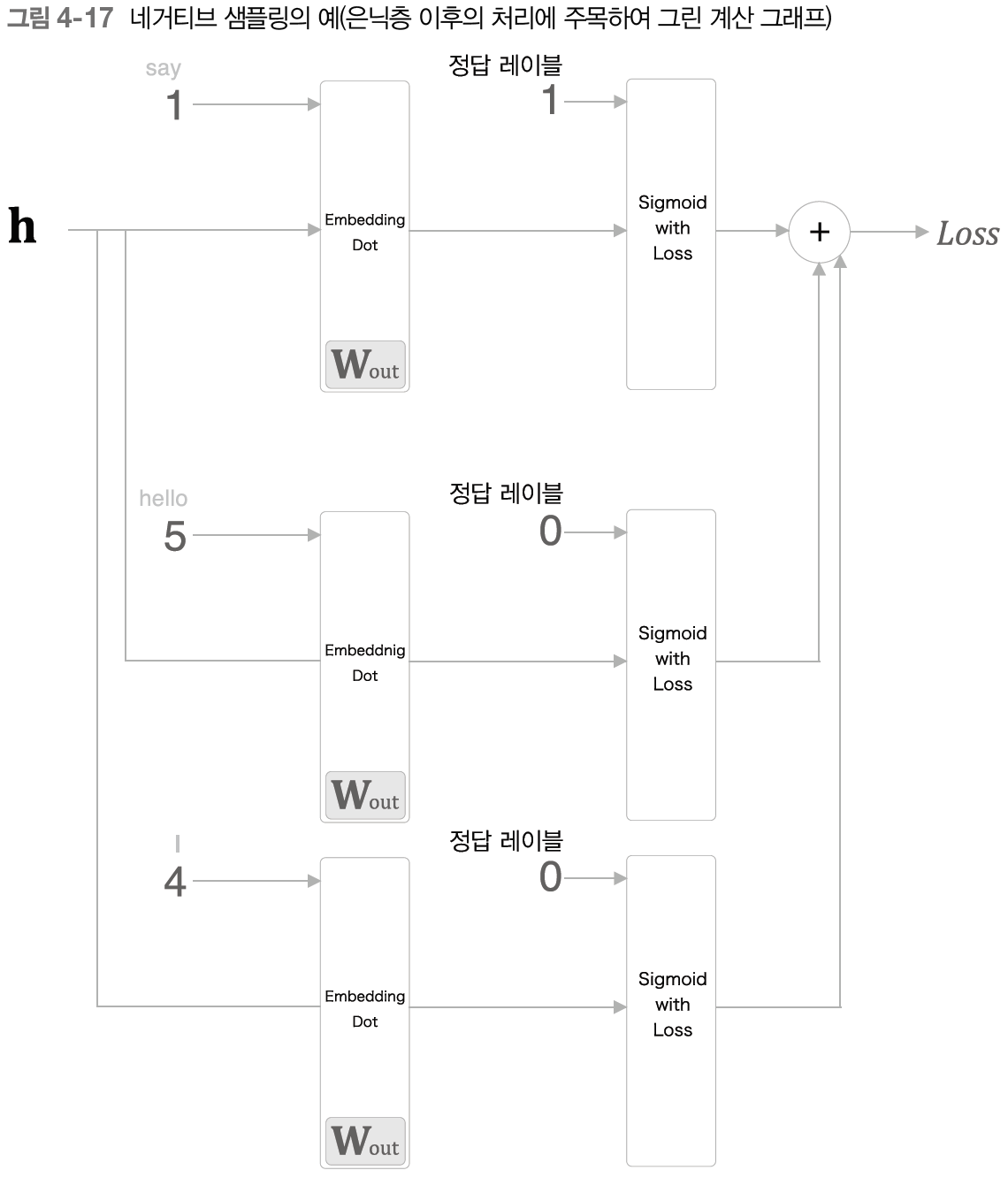
오답에 대한 학습에서 정답 레이블에는 0이 들어간다. 정답 레이블은 타깃이 실제로 정답인지 아닌지를 나타낸다.

위 그림에서 정답과 오답을 동시에 다룬다. 각 데이터의 손실을 모두 더해 최종 손실을 출력하면 된다.

4.2.6 - 네거티브 샘플링의 샘플링 기법

오답을 샘플링하는 기법에서, 무작위로 샘플링하는 것보다 좋은 방법이 존재한다. 바로 corpus의 통계 데이터(확률분포)를 기초로 샘플링하는 방법이다.

구체적으로는, corpus에서 자주 등장하는 단어를 많이, 드물게 등장하는 단어를 적게 추출하는 것이다. 희소한 단어만 샘플링해서 사용하게 되면 결과는 당연히 좋지 않기 때문이다.

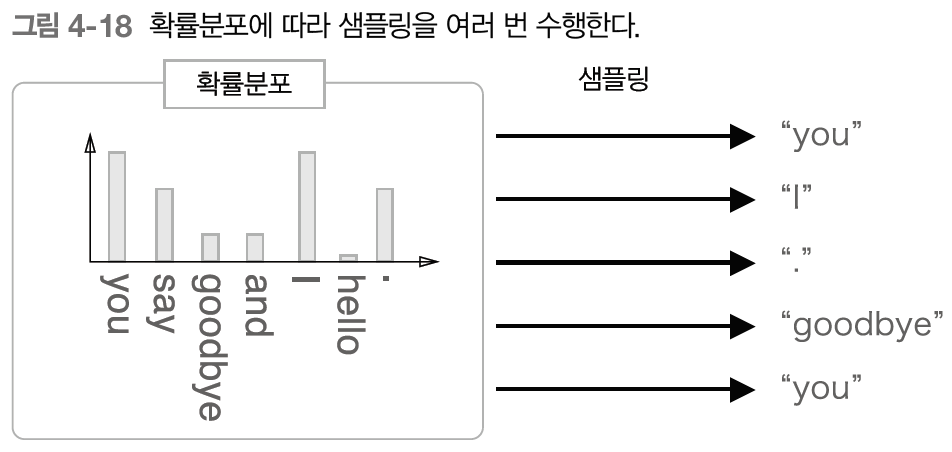
corpus에서 각 단어의 출현 횟수를 구해 확률분포로 나타내고 그 확률대로 단어를 샘플링하면 된다. 그러면 자연스럽게 자주 등장하는 단어는 샘플링될 확률이 높고, 희소한 단어는 샘플링될 확률이 낮아진다.

다만 실제로 구현할 때는 확률분포에 약간의 수정을 더한다.

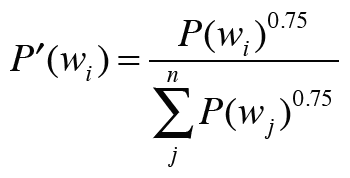
원래의 확률분포에 0.75제곱을 해주는 것이다. 출현 확률이 낮은 단어의 확률을 약간 높임으로써 단어를 버리지 않는 것이다.