이진 탐색 이란?

단순 순차탐색을 하게 되면 O(N)의 시간복잡도를 갖게 된다. 좀 더 큰 수를 좀 더 빠르게 탐색하기 위해서는 이진 탐색을 써야 한다.
이진 탐색은 탐색 범위를 절반씩 좁혀가며 빠르게 찾을 수 있지만, 데이터가 정렬된 상태에서만 사용할 수 있다. 이진 탐색을 이용했을 때 시간복잡도는 log(N)이다.

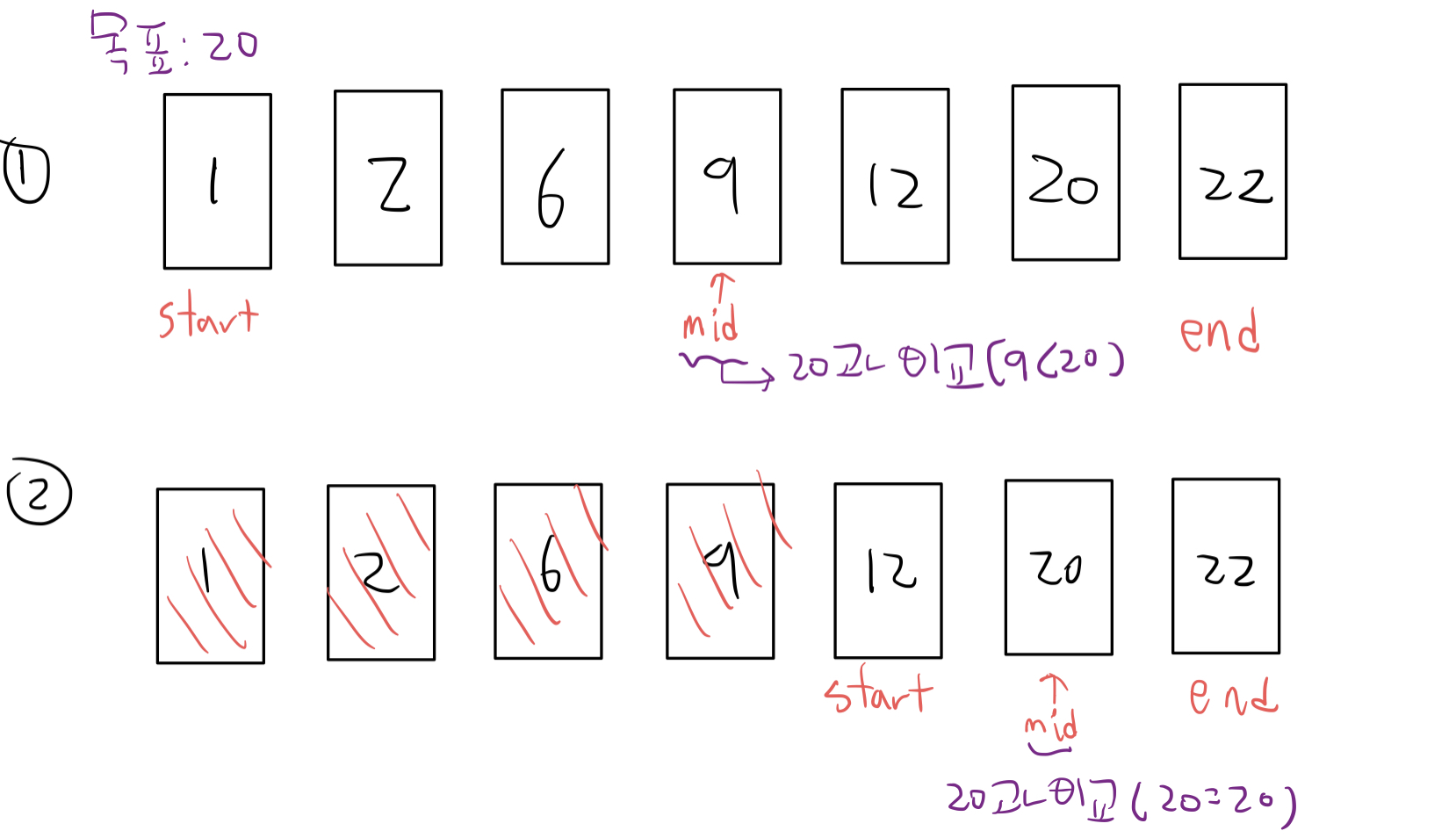
이진 탐색은 재귀 함수를 이용하거나 반복문을 이용해 구현할 수 있다.

재귀 함수 구현

arr = [1, 2, 6, 9, 12, 20, 22]

def binarySearch(start, end, target):
  if start > end:
    return None
  mid = (start + end) // 2
  if arr[mid] == target:
    return mid
  elif arr[mid] > target:
    return binarySearch(start, mid - 1, target)
  elif arr[mid] < target:
    return binarySearch(mid + 1, end, target)

ans = binarySearch(0, 6, 20)

print(ans)
-> 5

but, 재귀 특성상 효율성이 떨어질 수 있다.

반복문 구현

arr = [1, 2, 6, 9, 12, 20, 22]

def binarySearch(start, end, target):
  while start <= end:	# 재귀랑 반대의 등호
    mid = (start + end) // 2
    if arr[mid] == target:
      return mid
    elif arr[mid] > target:
      end = mid - 1
    elif arr[mid] < target:
      start = mid + 1
  return None
      
ans = binarySearch(0, 6, 20)

print(ans)
-> 5

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 지음