정렬?

데이터를 특정한 기준에 따라 순서대로 나열하는 것.
정렬의 종류로는 선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬 등이 있다.

선택 정렬

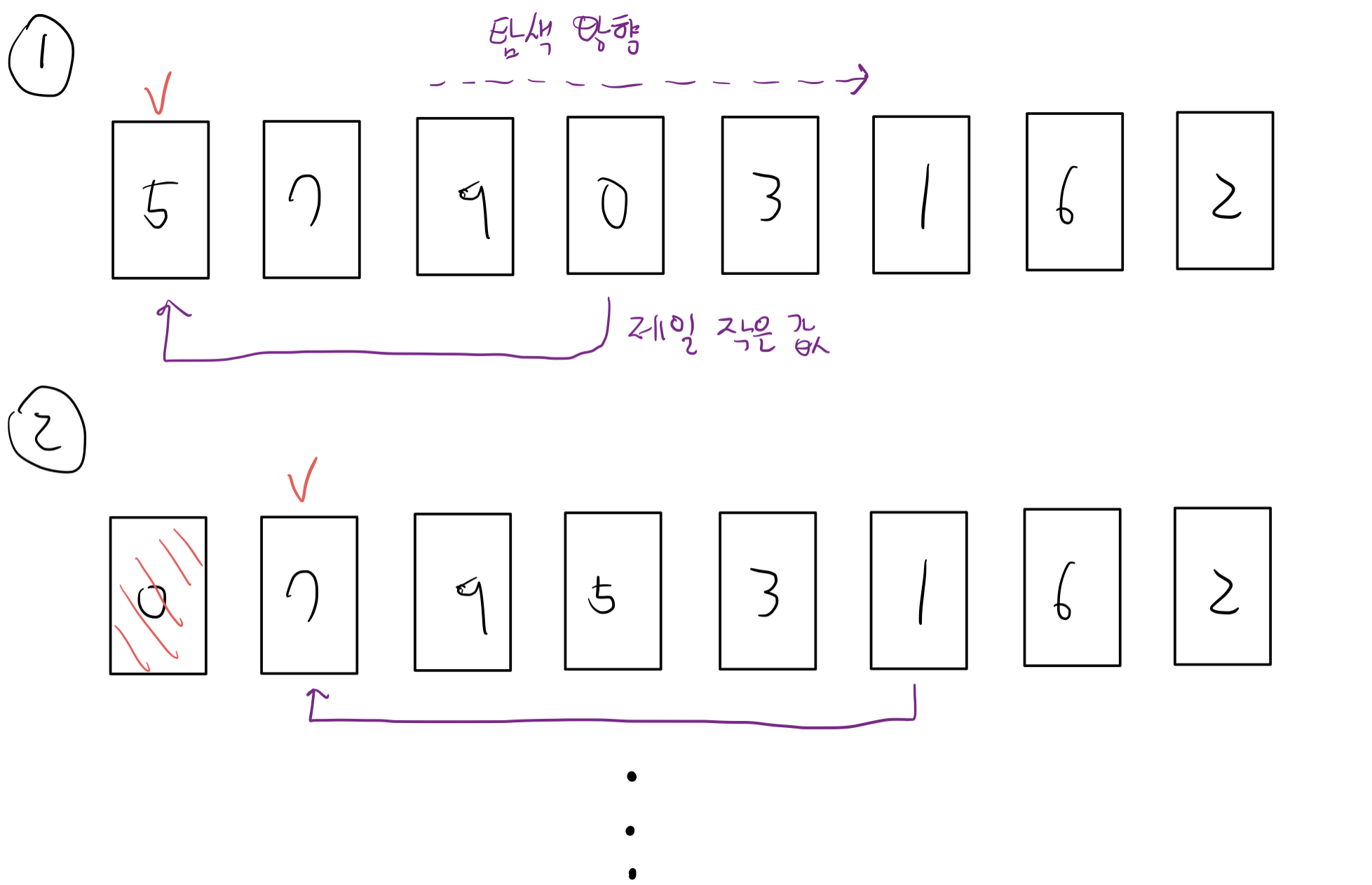
index 0부터 시작하여, 가장 작은 데이터를 선택해 맨 앞(기준)에 있는 데이터와 바꿔준다.
초기 상태와 관계없이 일정하게 탐색하므로, 데이터의 개수를 N이라 할때 시간 복잡도는 O(N^2)이다.

arr = [5, 7, 9, 0, 3, 1, 6, 2]

for i in range(8):
  minVal = arr[i]
  idx = i
  for j in range(i, 8):
    if minVal > arr[j]:
      minVal = arr[j]
      idx = j
  arr[i], arr[idx] = arr[idx], arr[i]

삽입 정렬

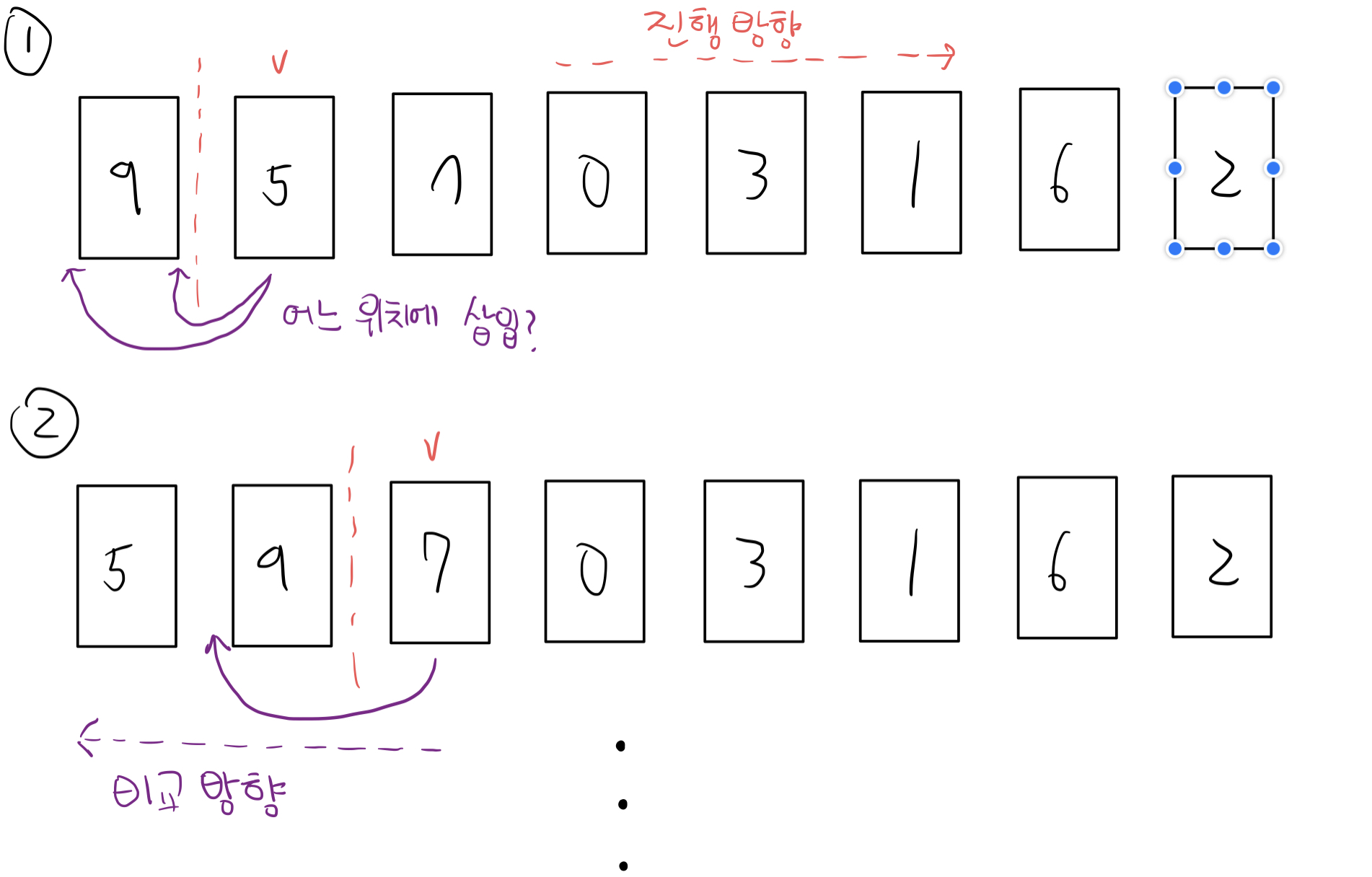
index 1부터 시작하여, 기준 데이터를 정렬이 완료된 앞 부분과 비교하여 적절한 위치에 삽입시킨다. 단, 비교할때 앞 부분은 오름차순으로 정렬돼있으므로 왼쪽으로 이동하며 기준 데이터보다 작은 데이터를 만났을때 그 자리에서 비교를 멈추면 된다.
평균 시간 복잡도는 O(N^2)이지만, 기존 리스트가 정렬이 거의 된 상태에서는 O(N)으로 빠르게 동작한다(비교할때마다 그 자리에서 바로 멈춘다).

arr = [5, 7, 9, 0, 3, 1, 6, 2]

for i in range(1, 8):
  for j in range(i, 0, -1):
    if arr[j] < arr[j-1]:
      arr[j], arr[j-1] = arr[j-1], arr[j]
    else:
      break

퀵 정렬

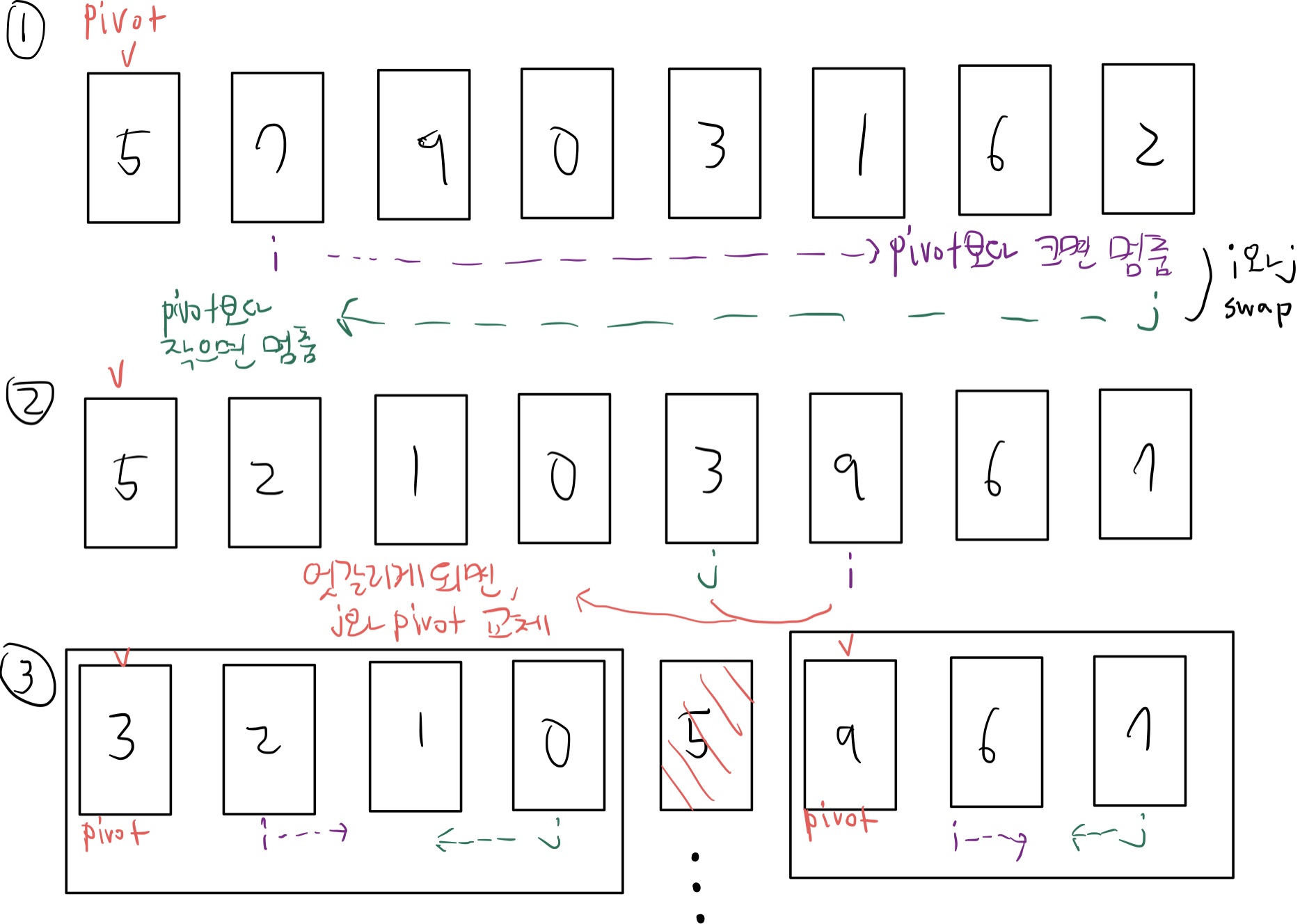
맨 앞 데이터를 pivot으로 설정하여, 양쪽에서 pivot과 비교하여 멈추면 swap 해준다. 단, 양쪽(i와 j)이 엇갈리게 되면, pivot과 j를 바꿔준다. 그 후 pivot으로 갈라진 양쪽에서 이 과정을 반복해준다.
평균 시간 복잡도는 O(NlogN)이지만, 기존 리스트가 정렬이 거의 된 상태에서는 O(N^2)으로 느리게 작동한다(j가 다가와서 자기 자신과 자리를 바꾸므로 매번 full로 탐색함).
기본 제공 라이브러리에서는 추가적인 로직으로 최악의 경우에도 O(NlogN)을 보장해준다고한다.

arr = [5, 7, 9, 0, 3, 1, 6, 2]

def QuickSort(start, end):
  if start >= end:
    return
  pivot = start
  i = start + 1
  j = end
  while i <= j:
    while i <= end and arr[i] <= arr[pivot]:	# 등호 주의!
      i += 1
    while j > start and arr[j] >= arr[pivot]:
      j -= 1
    if i > j:
      arr[pivot], arr[j] = arr[j], arr[pivot]
    else:
      arr[i], arr[j] = arr[j], arr[i]
      
  QuickSort(start, j-1)
  QuickSort(j+1, end)

QuickSort(0, 7)

계수 정렬

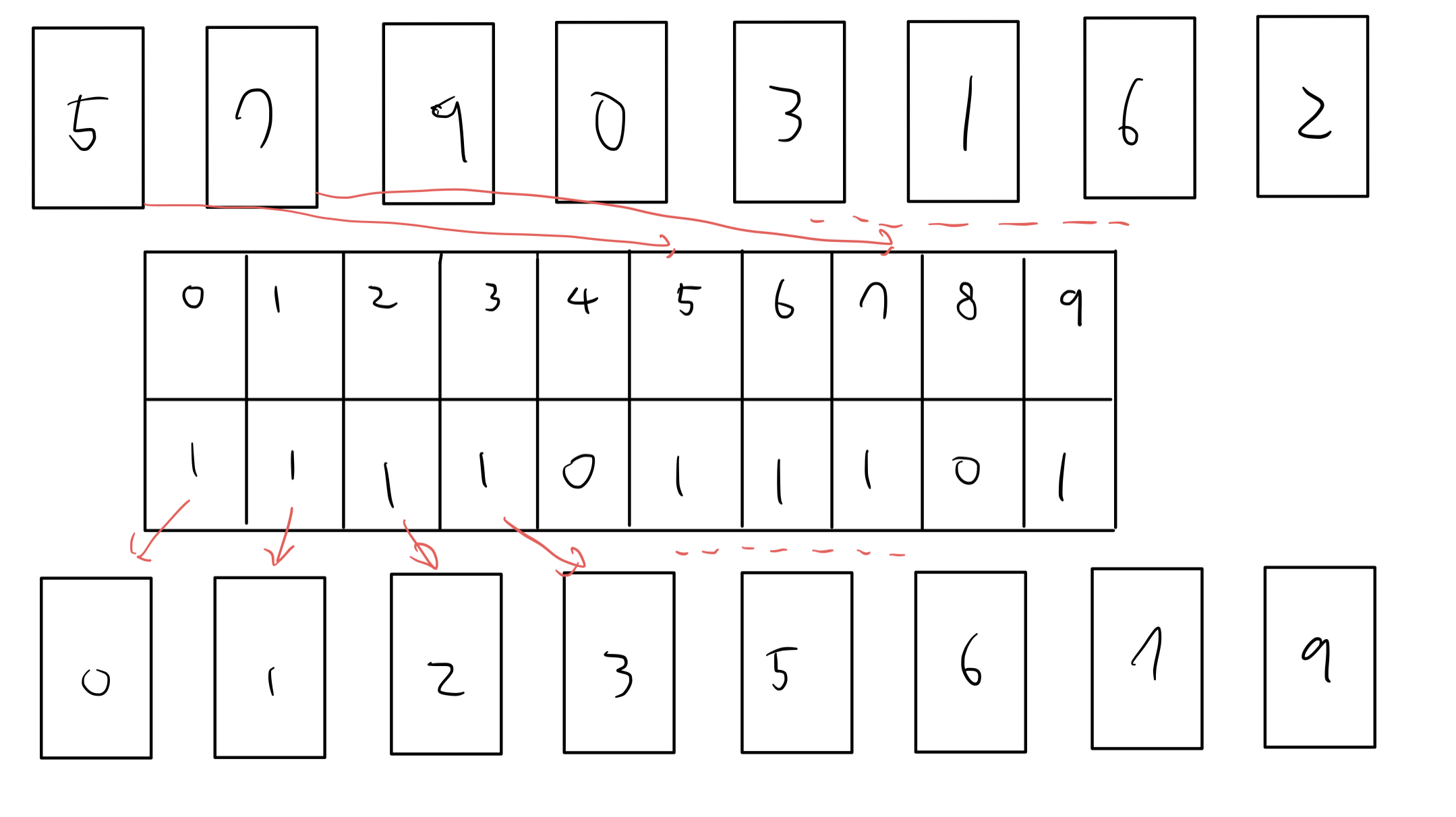
계수 정렬은 모든 데이터가 양의 정수일때만 가능한 매우 빠른 정렬 알고리즘이다. 모든 범위를 담는 리스트를 선언해주고 그 안에 맞게 담으면 되는데, 가장 작은 데이터와 가장 큰 데이터의 차이가 너무 크면 사용할 수 없다.
데이터 중 최댓값을 K라고 하면 시간 복잡도는 O(N+K)이다.

arr = [5, 7, 9, 0, 3, 1, 6, 2]
countArr = [0] * 10
sortArr = [0] * 8

for i in range(8):
  countArr[arr[i]] += 1

k = 0
for i in range(10):
  while countArr[i] > 0:
    sortArr[k] = i
    k += 1
    countArr[i] -= 1

print(sortArr)

Reference

이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 지음