[CS] 데이터

Judevv·2023년 5월 25일

데이터 혼자공부하는컴퓨터구조+운영체제

혼자 공부하는 컴퓨터 구조 + 운영체제

목록 보기

2/4

데이터

학습 목표

컴퓨터가 이해하는 정보단위를 이해한다.

0과 1로 다양한 숫자를 표현하는 방법을 이해한다.

0과 1로 다양한 문자를 표현하는 방법을 이해한다.

0과 1로 숫자를 표현하는 방법

핵심 키워드 : 비트 바이트 이진법 2의 보수 십육진법

정보 단위

컴퓨터는 0과 1로 모든 정보를 표현하고, 0과 1로 표현된 정보만을 이해할 수 있다.

비트(bit) : 0과 1을 나타내는 가장 작은 정보 단위

n비트로 2의 n제곱까지의 정보 표현 가능
프로그램은 수많은 비트로 이루어져 있음

큰 수의 비트(프로그램의 크기 등)를 말한땐 비트보다 더 큰 단위를 사용

1바이트(1byte)	8비트(8bit)
1킬로바이트(1KB)	1,000바이트(1,000byte)
1메가바이트(1MB)	1,000킬로바이트(1,000KB)
1기가바이트(1GB)	1,000메가바이트(1,000MB)
1테라바이트(1TB)	1,000기가바이트(1,000GB)

1024개씩 묶은 단위는 KiB, MiB, GiB

💡) 비트 쉽게 이해하기
전구에 빗대면, 전구 하나로 두 가지 상태(켜짐, 꺼짐)를 표현
1비트는 한 개의 전구, 0 또는 1, 두 가지 정보를 표현
2비트는 두 개의 전구, 네 가지 정보를 표현
3비트는 세 개의 전구, 여덟 가지의 정보를 표현
...

💡) 워드(word)
워드(word)란 CPU가 한 번에 처리할 수 있는 데이터의 크기를 의미한다.
만약 CPU가 한 번에 16비트를 처리할 수 있다면 1워드는 16비트가 되는 것이다.
워드의 절반 크기를 하프 워드(half word), 1배 크기를 풀 워드(full word), 2배 크기를 더블 워드(double word)라고 한다.

이진법(binary)

0과 1만으로 모든 숫자를 표현하는 방법을 말한다.

이진수 표현
- 숫자가 1을 넘어가는 시점에 자리 올림
- 일상적으로 사용하는 십진법은 9가 넘어갈 때 자리를 올림
- 이진수 표기 : 100101(2) 0b100101
- 음수 표기 : 2의 보수 표현
  - 어떤 수를 그보다 큰 2의 n제곱에서 뺀 값 = 모든 0과 1을 뒤집고 1을 더한 값
컴퓨터가 음수로서의 이진법과 십진수를 표현하기 위한 양수로서의 이진법을 구분하는 방법
- CPU 내부에 플래그(flag) 레지스터가 구분
- 컴퓨터 내부의 숫자들은 자신이 음수인지, 양수인지 어떤 깃발(플래그)을 들고 다님

💡) 2의 보수 표현의 한계
그렇다면 플래그만 바뀌어도 될 것 같은데, 왜 굳이 2의 보수 표현으로 음수를 나타내는 걸까?

0이나 2의 제곱 형태의 이진수에 2의 보수를 취하면 원하는 음수 값을 얻을 수 없기 때문이다.

0을 음수로 표현할 경우, '0000(2)'의 모든 0과 1을 뒤집으면 '1111(2)'이 되는데, 거기에다가 1을 더하면 '10000(2)'이 된다. 이 경우 자리 올림으로 발생한 비트의 1을 버리지만,

2의 3제곱을 음수로 표현할 경우, '1000(2)'의 모든 0과 1을 뒤집으면 '0111(2)'이 되는데, 거기에다가 1을 더하면 '1000(2)'로 양수로 표현한 값과 같아, 2의 보수를 취한 값이 자기 자신이 되어버리는 문제가 발생한다.

따라서, n비트로는 -2의 n제곱과 2의 n제곱이라는 수를 동시에 표현할 수 없기 때문이다.

십육진법(hexadecimal)

이진법은 0과 1만으로 모든 숫자를 표현하다 보니 숫자의 길이가 너무 길어진다는 단점이 있다. 그래서 십육진법을 자주 사용하기도 한다.

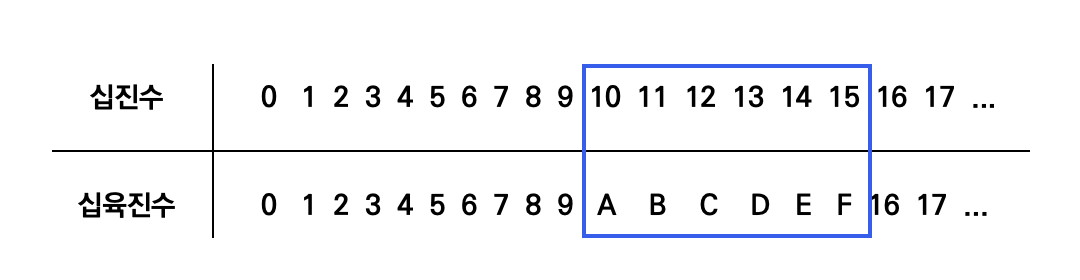
십육진수 표현
- 십진수와 1~9까지는 동일함
- 10~15까지 각각, A~F로 표현
- 수가 15를 넘어가는 시점에 자리 올림
- 십육진수 표기 : 15(16) 0x15

십육진수를 이진수로 변환하기

십육진수 한 글자를 4비트의 이진수로 간주한다.
십육진수를 이루고 있는 각 글자를 따로 따로 이진수로 변환하고, 그것을 그대로 이어 붙인다.

ex) 1A2B(16) = 0001 1010 0010 1011(2)

이진수를 십육진수로 변환하기

이진수 숫자를 네 개씩 끊고, 끊어 준 네 개의 숫자를 하나의 십육진수로 변환한 뒤 그대로 이어붙인다.

ex)
1101(2) = D(16)
0101(2) = 5(16)
11010101(2) = D5(16)

💡) 코드에 십육진수를 직접 넣는 사례
십육진수는 개발 분야에서 코드에 십육진수를 직접 쓰는 경우도 더러 있다.
// 예시 코드
offset = __mem_to_opcode_arm(*(u32 *)loc);
offset = (offset & 0x00ffffff) << 2;
if (offset & 0x02000000)
offset -= 0x04000000;
offset += sym->st_value - loc;

0과 1로 문자를 표현하는 방법

문자 집합과 인코딩

문자 집합 : character set
- 컴퓨터가 인식하고 표현할 수 있는 문자의 모음
인코딩 : encoding
- 코드화 하는 과정
- 문자를 0과 1로 이루어진 문자 코드로 변환하는 과정
디코딩 : decoding
- 코드를 해석하는 과정
- 0과 1로 표현된 문자 코드로 문자로 변환하는 과정

아스키 코드

초창기 문자 집합 중 하나
영어 알파벳, 아라비아 숫자, 일부 특수 문자 및 제어 문자를 포함
7비트로 하나의 문자를 표현
- 8비트 중 1비트는 오류 검출을 위해 사용됨(패리티 비트, patity bit)
- 128(2의 7제곱)개 정도의 문자 표현 가능
코드 포인트 : 문자에 부여된 값
장점과 단점
- 장점 : 간단한 인코딩
- 단점 : 한글을 포함한 다른 언어 문자나 다양한 특수 문자 표현 불가(7비트, 128개 한계)

EUC-KR

한글의 인코딩을 이해하려면 한글의 특수성을 알아야 한다

한글의 특징
- 각 음절 하나하나가 초성, 중성, 종성의 조합으로 이루어짐
한글 인코딩 방식
- 완성형 인코딩
  - 초성, 중성, 종성의 조합으로 이루어진 하나의 글자에 고유한 코드 부여
- 조합형 인코딩
  - 초성, 중성, 종성 각각에게 비트열을 부여
EUC-KR
- 완성형 인코딩
- 각 글자에 2바이트(십육진수 4개) 크기의 코드를 부여
- 2,350개 정도의 한글 단어를 표현할 수 있음
- but, 모든 한글 조합을 표현할 수 없음(예를 들어, '쀍', '쀓' 같은 글자)

유니코드와 UTF-8

언어별 인코딩은 다국어를 지원하는 프로그램을 개발할 때, 언어별 인코딩 방식을 모두 이해해야 한다.(예를 들면, 한글 처럼)

유니코드
- 통일된 문자 집합
- 한글, 영어, 화살표, 이모티콘까지도 코드로 표현할 수 있음
- 현대 문자 표현에 있어 매우 중요
- 코드 포인트 : 각 문자별로 고유한 16진수(4자리)가 부여됨
- 인코딩 방식(UTF)
  - UTF-8
    - 가변 길이 인코딩 : 인코딩 결과가 1바이트 ~ 4바이트(유니코드에 부여된 값에 따라 다름)
  - UTF-16, UTF-32