크로스 엔트로피

신경망 학습을 위한 손실 함수

일반적으로
회귀문제: MSE
분류문제: CrossEntropy or BinaryCrossEntropy

정보량, 엔트로피, 크로스 엔트로피

• 정보량
  사건이 얼마나 자주 발생하는지
• 엔트로피
  확률 변수가 얼마나 불확실한지
• 크로스 엔트로피
  두 분포의 차이가 어느 정도인지 판단

정보량

정보는 놀라움의 정도에 비례한다.
확률이 낮은 사건이 발생하면 놀라움의 정도가 커지므로 정보가 많다고 볼 수 있다.

따라서 정보량은 확률에 반비례하면서 독립 사건들의 정보량은 더해져야 하므로, 정보량은 확률의 역수에 로그를 취한 값으로 정의된다.

엔트로피

엔트로피란 확률 변수 또는 확률 분포가 얼마나 불확실한지를 나타낸다.

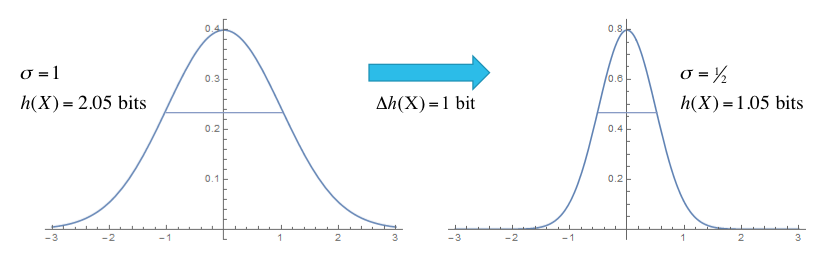
(적당한 사진이 없어서 그냥 모양만 보자)
왼쪽 그래프는 분산이 큰 확률분포로, 넓은 범위에서 사건이 발생하기 때문에 어떤 사건이 발생할지 불확실하다. 따라서 엔트로피가 높은 상태이다

오른쪽 그림은 분산이 작은 확률분포로 좁은 범위에서 사건이 발생하기 때문에 어떤 사건이 발생할지 확실하다. 따라서 엔트로피가 낮은 상태이다

엔트로피와 분산은 비례한다

크로스 엔트로피

두 확률분포의 차이

확률 분포 q로 확률분포 p를 추정한다고 해보자.
크로스 엔트로피는 q의정보량을 p에 대한 기댓값을 취하는 것으로 정의된다.

q가 p를 정확히 추정해서 두 분포가 같아지면 크로스 엔트로피는 최소화되고, q가 p를 잘 못 추정하면 크로스 엔트로피는 높아진다.

솔직히 어떤 말인지 자세하게는 이해가 안간다.

결국에 일반적인 수식은 다음과 같다.

• Binary Class 분류

  $l = -(1 * log(p))$

• N class에 대한 다중 분류

  $-\sum_{c=1}^{N}y_clog(p_c)$