4장 최적화 알고리즘 (1)

최적화란?

• 학습률(Learning Rate)을 적당히 조정해가며 최적해를 찾는 것

최적화의 발달 단계는 다음과 같으며 SGD를 기반으로 한다.
SGD Momentum -> 네스테로프 모멘텀 -> AdaGrad -> RMS Prop -> Adam

최적화를 본격적으로 보기전에 손실함수에서 나타날 수 있는 문제점인 안장점에 대해 알고 시작하자.

Saddle Point(안장점)

손실 함수의 곡면에서 임계점(critical point)은 미분값이 0인 지점으로 최대점, 최소점, 안장점이 있다.

안장점이란?

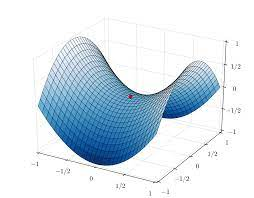
하나의 축에서 볼땐 최소점이었지만, 다른 하나의 축에서 볼땐 최대점이 되는 지점
(손실함수에서 안장점은 굉장히 많을 수 있다.)

임계점을 만났을 때 최대, 최소, 임계점은 어떻게 구분하는가?

임계점에서 손실을 확인해보면 어느정도 구분할 수 있다.

손실이 매우 낮으면 최소점, 매우 높다면 최대점일 가능성이 크며, 손실이 수렴했다고 보기에 매우 낮지 않으면 안장점이라고 추정할 수 있다.

손실함수의 차원이 높을수록 안장점을 쉽게 만날수 있는 만큼, 확률적 경사하강법이 학습을 중단할 가능성도 커진다. 다행히 안장점은 최대와 최소가 만나는 지점이므로 약간의 관성을 통해 쉽게 탈출할 수 있다.

확률적 경사하강법 (SGD)

SGD란 mini batch를 사용하여 확률적으로 경사하강을 하는 방법을 의미한다.

확률적 경사하강법의 단점
폭이 좁고 깊은 협곡 모향의 loss형태에서 양옆으로 진동만하고 아래쪽으로는 잘 내려가지 못한다.

SGD Momentum

SGD에 관성을 주어 느린 학습속도와 안장점에 대한 문제를 해결한 알고리즘이다.

핵심 개념

SGD 모멘텀은 현재의 속도 벡터와 그래디언트 벡터를 더해서 다음 위치를 정한다.

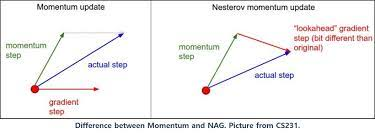(그림에서 좌측)

관성이 작용하며 학습 경로가 전체적으로 매끄러워지고 가속도가 생겨 학습이 매우 빨라진다.

수식은 다음과 같이 2가지로 표현할 수 있다.
$v_t$: 속도
$\rho$: 마찰 계수 (보통 0.9나 0.99를 사용한다)

두 수식은 속도를 계산할 때 gradient 누적방향이 반대라는 점이며, 이에 따라 파라미터 업데이트 방향도 반대로 되어 있다.

OverShooting

경사가 가파르면 빠른속도로 내려오다가 최소 지점을 만나면 그래디언트는 순간적으로 작아지지만 속도는 여전히 크기때문에 최소지점을 지나치는 것

이를 막기위해 최적해 주변을 평평하게 만들어주는 정규화 기법을 사용할 수 있다.

네스테로프 모멘텀

SGD 모멘텀에 오버 슈팅을 막기 위해 현재 속도로 한걸음 미리 가보고 오버 슈팅이 된 만큼 다시 내리막길로 내려가기 때문에 이동 방향에 차이가 있다. (위 SGD Momentum 수식에서 (2)번을 사용)

수식은 다음과 같다.

다음 속도 $v_{t+1}$은 현재 속도에 마찰 계수를 곱한 뒤 현재 속도로 한걸음 미리 가본 위치의 gradient를 빼서 계산한다.

gradient 계산 트릭

한 걸음 미리 가본 지정믜 gradient를 계산하려면, 한걸음 미리 갔다가 돌아와야 하기 때문에 계산이 조금 복잡하다. 계산을 단순화하기 위해 미리 가본 위치를 현재 위치로 바꾸는 트릭을 사용할 수 있다.

이 트릭의 핵심 아이디어는 $x_t + \rho v_t$를 새로운 변수 $\tilde{x}_t = x_t+\rho v_t$로 치환하는 것이다.

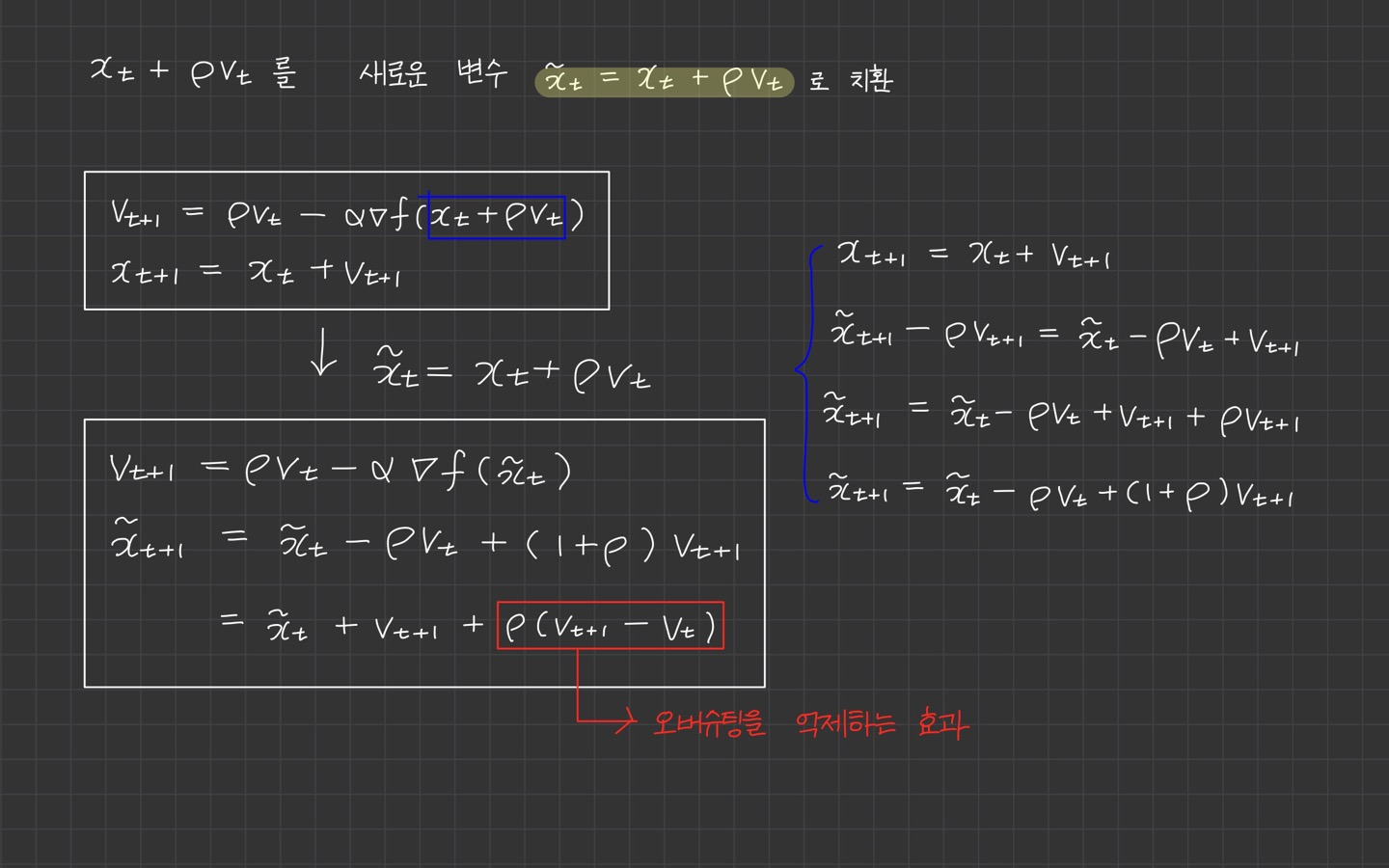
SGD Momentum의 2번째 식과 거의 동일한 식이며 마지막에 오버슈팅을 억제해주는 $\rho(v_{t+1} - v_t)$만 추가 되었다.

AdaGrad (Adaptive Gradient)

AdaGrad는 손실 함수의 곡면의 변화에 따라 적응적으로 학습률을 정하는 알고리즘이다.

핵심 개념

손실 함수의 경사가 가파를 때 작은 폭으로 이동하고, 경사가 완만하면 큰 폭으로 빠르게 이동하자. 이를 위해 곡면의 변화량에 학습률이 적응적으로 조정되어야 한다.

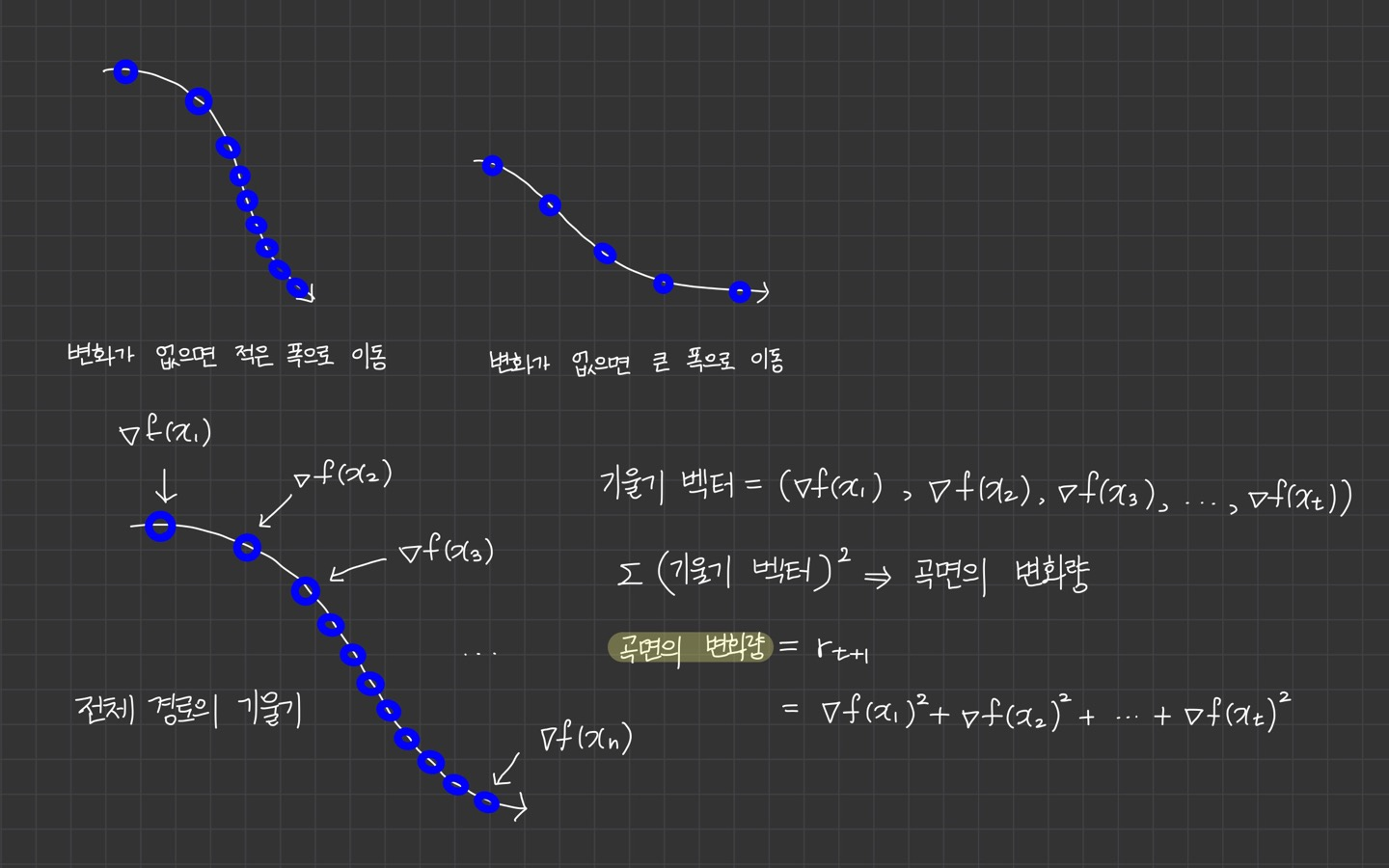
먼저 모든 단계의 기울기를 하나의 벡터로 표현하면 이와 같다.

각 기울기의 제곱합을 계산해서 곡면의 변화량으로 사용할 수 있다.

제곱합의 효과
1. 기울기의 방향을 고려하지 않고 크기만 고려할 때 사용할 수 있다.
2. 상대적인 차이를 강조할 수 있다.

SGD의 파라미터 업데이트 식에서 학습률 $\alpha$를 곡면의 변화량의 제곱근 $\sqrt{r_{t+1}}$로 나눠주면 적응적 학습률이 된다.

적응적 학습률은 곡면의 변화량에 반비례하므로, 곡면의 변화가 크면 천천히 학습하고, 곡면에 변화가 적으면 빠르게 학습한다.

$r_{t+1}$: 그래디언트 제곱의 합
${\alpha \over{\sqrt{r_{t+1}}+\epsilon}}$: 곡면이 변화량을 반영하는 적응적 학습률
$\nabla f(x_t)$: 그래디언트

학습 초반에 학습이 중단되는 현상

AdaGrad는 곡면의 변화량을 전체 경로의 기울기 벡터의 크기로 계산하므로 학습이 진행될수록 곡면의 변화량은 점점 커지고 반대로 적응적 학습률은 점점 낮아진다.

만일 경사가 매우 가파른 위치에서 학습을 시작하면 초반부터 적응적 학습률이 급격히 감소하기 시작해서 조기에 학습이 중단될 수 있다. 이를 해결하기 위해 RMSProp이 제안되었다.

(2장에 계속)

참고

• https://velog.io/@cha-suyeon/DL-%EC%B5%9C%EC%A0%81%ED%99%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98