4장 최적화 알고리즘 (2)

꼼댕이·2023년 6월 20일

목록 보기

5/11

4장 최적화 알고리즘 (1)에서 Saddle point, SGD, SGD Momentum, Nesterov Momentum, AdaGrad에 대해 알아봤다.

중요한 것은 관성을 통해 saddle point에서 미분점이 0이되어 학습이 불가능해지는 것을 방지하고자 했던 것과, 학습 과정에서 이상한 곳에서 학습이 종료되는 것을 방지하고자 한다는 것이다.

이번 장에서는 남은 2개인 RMSProp과 Adam에 대해서 알아보자.

RMSProp

RMSProp (root mean square propagation)은 최근 경로의 곡면 변화량에 따라 학습률을 적응적으로 결정하는 알고리즘이다.

AdaGrad가 조기에 학습이 중단되는 문제를 해결하기 위해 RMSProp은 곡면 변화량을 개선된 방식으로 측정한다.

곡면 변화량을 측정할 때 전체 경로가 아닌 최근 경로의 변화량을 측정하면 곡면 변화량이 누적되어 계속해서 증가하는 현상을 없앨 수 있다.

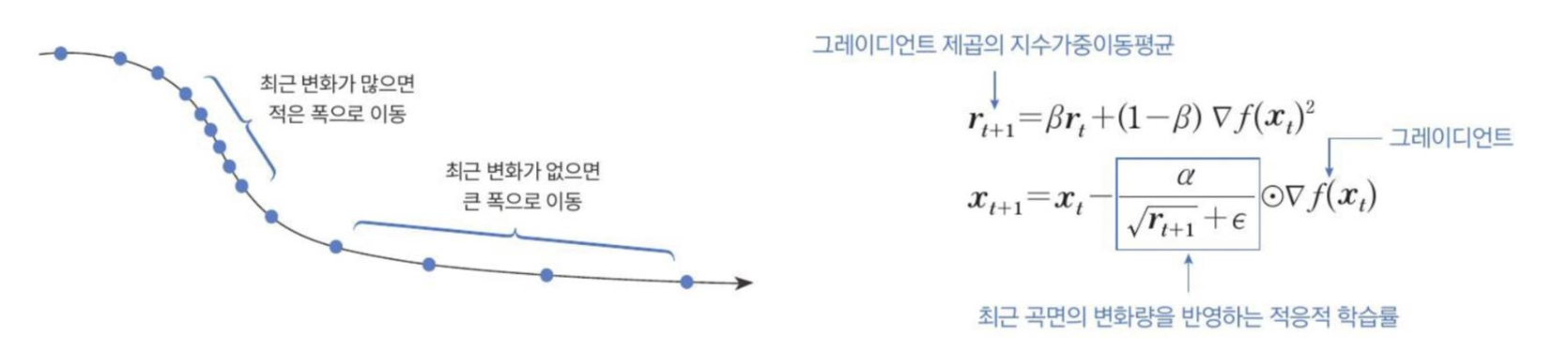
RMSProp은 최근 경로의 곡면 변화량을 측저앟기 위해 지수가중 이동평균을 사용한다.
다음 수식을 보면 $r_{t+1}$ 을 계산할 때 $r_t$ 와 gradient의 제곱 $\nabla f(x_t)^2$ 을 가중 합산해서 지수가중이동 평균을 계산했다.

r_{t+1} = \beta r_t + (1-\beta)\nabla f(x_t)^2 \\ x_{t+1} = x_t - {\alpha \over{\sqrt{r_{t+1}} + \epsilon}} \odot \nabla f(x_t)

$r_{t+1}$ : gradient 제곱의 지수가중 이동평균

${\alpha \over{\sqrt{r_{t+1}} + \epsilon}}$ : 최근 곡면의 변화량을 반영하는 적응적 학습률
$f(x_t)$ : gradient

이하는.. 수식이 많아서 이미지로 대체한다..

Adam(Adaptive moment estimation)은 SGD momentum과 RMSProp이 결합된 형태로, 진행하던 속도에 관성을 주고 동시에 최근 경로의 곡면의 변화량에 따라 적응적 학습률을 갖는 알고리즘이다.

최적화 성능이 우수하고, 잡음 데이터에 대해 민감하게 반응하지 않는다.
그리고 두 알고리즘을 합치면서 학습 초기 경로가 편향되는 RMSProp의 문제를 제거했다.

Adam을 식으로 표현하면,
(1) 1차 관성으로서 속도를 계산
(SGD 모멘텀의 첫번째 식에 해당하며, 속도에 마찰계수 $\rho$ 대신 가중치 $\beta_1$ 을 곱해 gradient의 지수가중이동평균을 구하는 형태로 수정)

(2) 2차 관성으로서 $gradient^2$ 지수가중이동평균을 구하는 식
(RMSProp의 첫번째 식과 동일하다)

(3) 파라미터 업데이트 식으로 1차 관성과 2차 관성을 사용

(가중치 $\beta1$ 과 $\beta2$ 는 보통 0.9나 0.99를 사용하며 $\epsilon$ 은 0이 되지 않게 더해주는 상수로 보통 1e-7이나 1e-8을 사용한다.)

v_{t+1} = \beta_1 v_t+(1-\beta_1) \nabla f(x_t)\ \ \ \ (1차 \ 관성(속도)) \\ \ \\ r_{t+1} = \beta_2 r_t+(1-\beta_2) \nabla f(x_t)^2\ \ \ \ (2차 \ 관성(gradient^2\ 지수가중이동평균)) \\ \ \\ x_{t+1} = x_t - {\alpha \over{\sqrt{r_{t+1}} + \epsilon}} \odot v_{t+1}

좀 더 자세한건 158p~ 확인해보자..

사람을 연구하는 공돌이