5-1장 초기화

초기화란?
신경망을 학습할 때 출발 위치를 결정하는 방법

가중치는 모델의 파라미터에서 가장 큰 비중을 차지하므로 가중치의 초기화 방법에 따라 학습 성능이 크게 달라질 수 있다.

잠깐 다시 한번 가중치 기초를 보자.

중요한 데이터를 선택하는 가중합산 연산(z)

뉴런에 입력데이터 $x^T$가 들어오면 가중치 $W^T$와 곱해서 가중합산(z)을 한다.

상수 초기화

가중치를 0으로 초기화

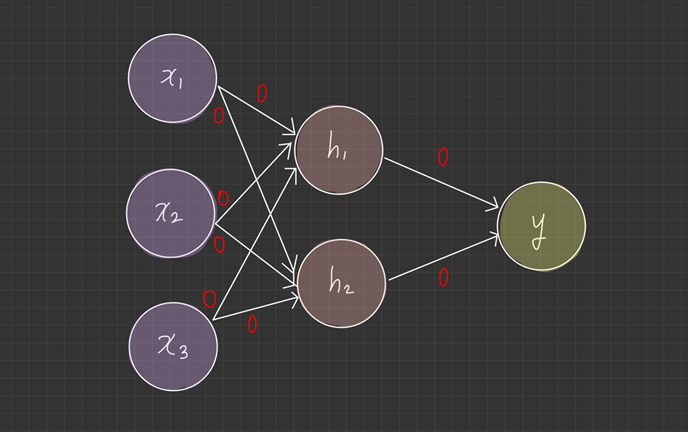
뉴런의 가중치가 0이면 가중 합산 결과는 항상 0이되고, 활성 함수는 가중합산 결과인 0을 입력받아 늘 같은 값을 출력한다.

항상 헷갈리던.. activation의 입력값은 가중합산의 결과이다.

if activation = ReLU, tanh: y=0
elif activation = sigmoid: y=0.5
elif activation = softmax: y=모든 클래스의 확률이 동일한 균등확률 분포

-> 즉 의미없는 결과이며, 가중치가 0이면 학습이 되지 않는다.

가중치가 0이 아닌 상수 초기화

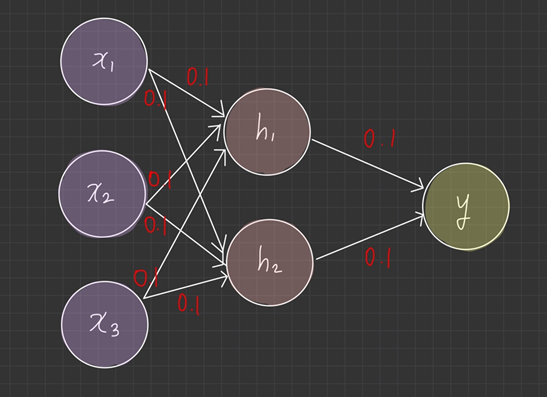
먼저 왜인지 모르겠지만 이 책에서는 입력 벡터 $x_1 = x_2 = x_3$를 가정한다.

$x_1 = x_2 = x_3\ \&\ w_1 =w_2=w_3=0.1$이기 때문에 가중합산 결과와 activation의 결과가 동일하며 여전히 의미가 없게된다.

가우시안 분포 초기화

상수로 모두 동일하게 초기화하는 것이 아닌 난수를 통해서 다르게 초기화하는 방식이다.

실험을 위해 다음과 같은 가정을 한다.
1. 각 layer에는 500개의 뉴런이 있고 총 10개의 layer를 사용한다.
2. activation function으로 tanh를 사용한다. (sigmoid계열)
3. 입력데이터는 크기가 500인 실수 벡터$x=(x_1 ,...x_{500})$이며 정규분포 $N(0,1)$을 따르는 난수이다.

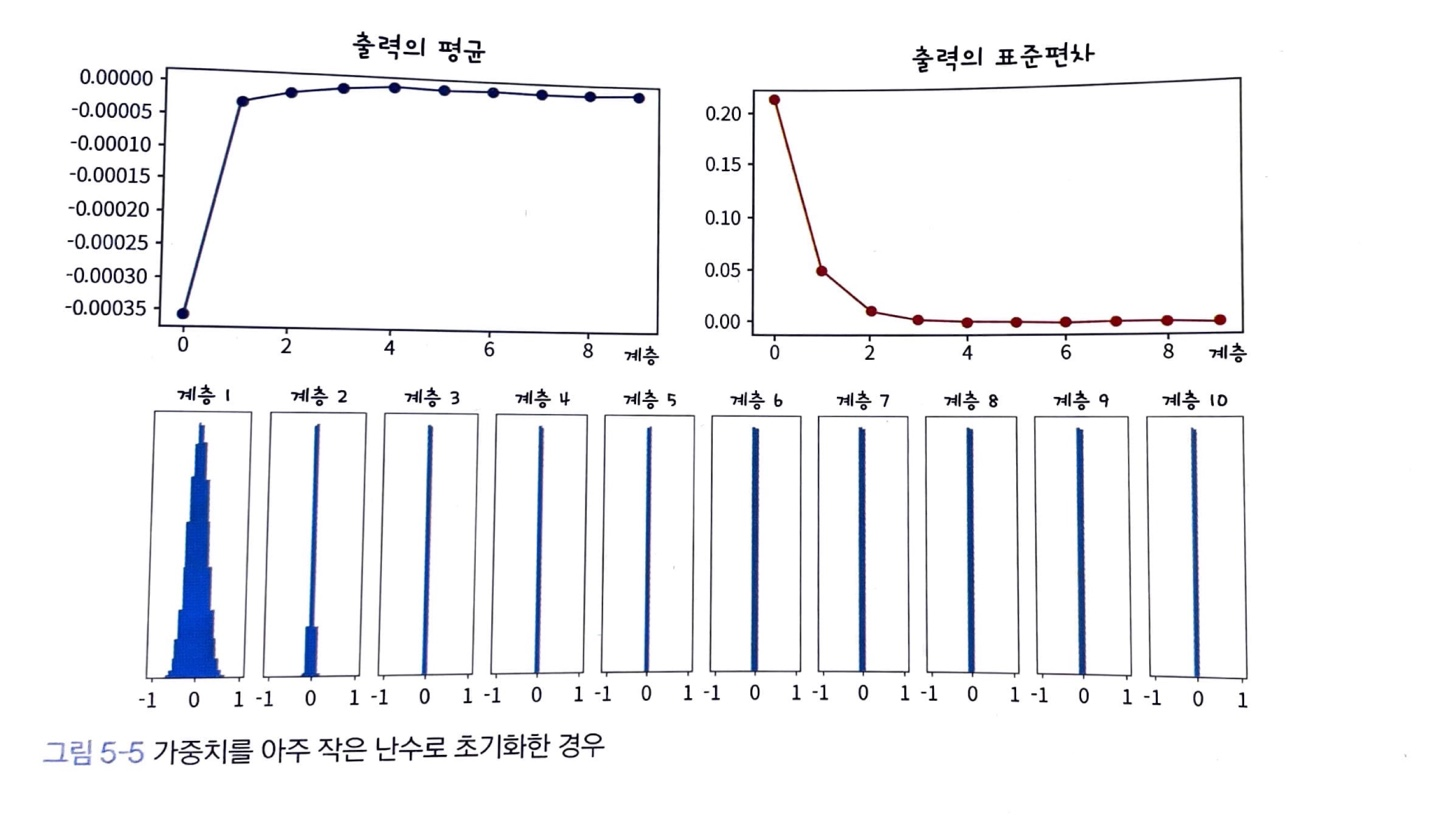
가중치를 아주 작은 수로 초기화 N(0, 0.01)

출력이 깊어질수록 점점 0으로 수렴한다

$w_1x_1 ...$에서 $w_1$이 굉장히 작은 값으로 들어가고 가중 합이 0에 가까워지며 0에 가까운 z가 activation function인 tanh(0.0...)이면 출력값이 0에 수렴하기 때문이다.

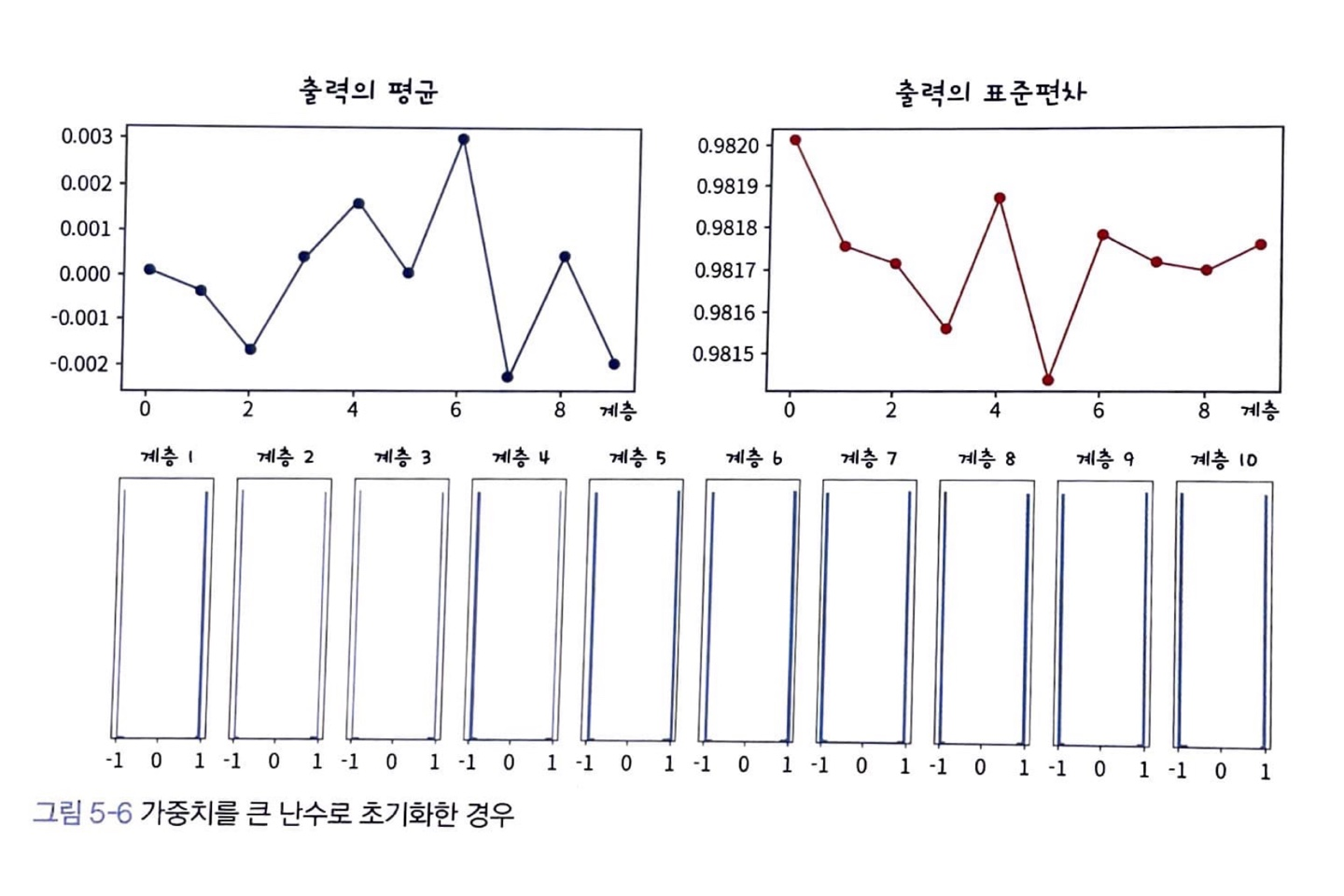
가중치를 큰 수로 초기화 N(0,1)

출력이 (1, -1)로 발산하게 된다.
tanh의 성질에 출력값이 양 극단에 가기 때문에 미분기울기가 0에 수렴하는 gradient vanishing 문제가 생긴다.

적절한 가중치란 무엇인가?

데이터가 layer를 거치더라도 데이터의 크기를 유지해주는 가중치
activation의 출력 결과도 고려하며 생각해야한다.

Xavier 초기화

시그모이드 계열 함수(sigmoid, tanh ...)를 사용할 때 가중치를 초기화하는 방법이다. (ReLU에서는 못쓴다.)

• 입력데이터의 분산이 출력데이터에서 유지되도록 가중치 초기화
• 데이터가 layer를 통과하더라도 같은 크기를 유지하려면 분산이 유지되어야 한다.

가정상황 1. 활성함수를 선형함수로 가정한다.

• 입력데이터가 0 근처의 작은 값으로 돼있을 때, 이 입력 데이터는 시그모이드 계열 함수의 가운데를 지난다.
• 시그모이드 계열의 가운데는 거의 선형이므로 선형함수로 가정한다.
  

(유도과정이 길어서 이미지로 대체한다.)

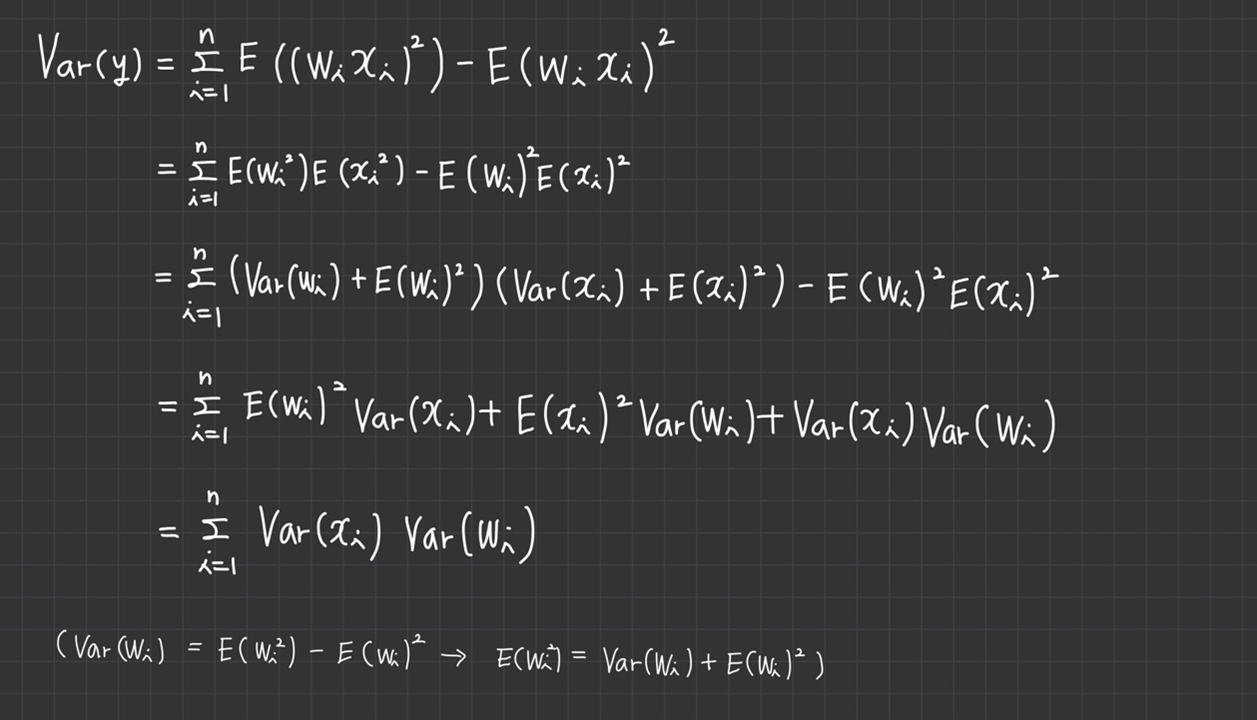
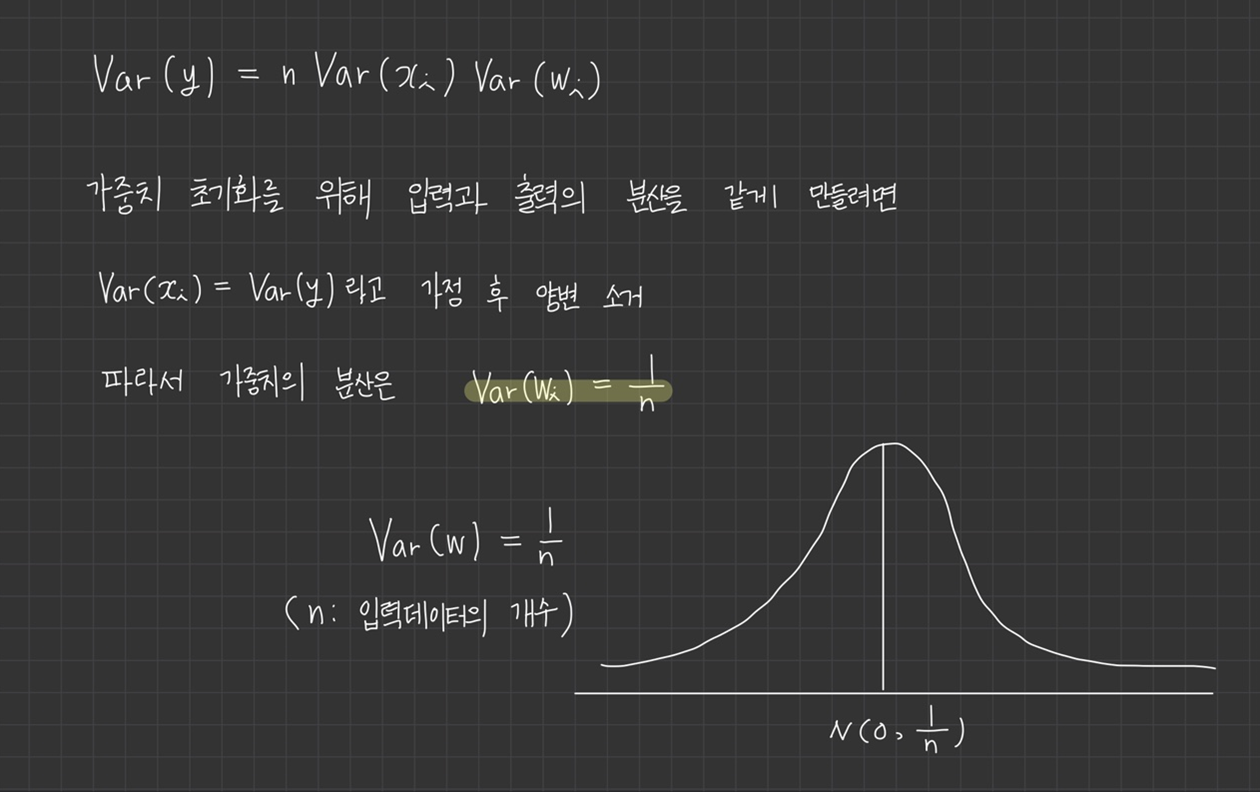
입력데이터 개수 n에 반비례하며 초기화하는 방식

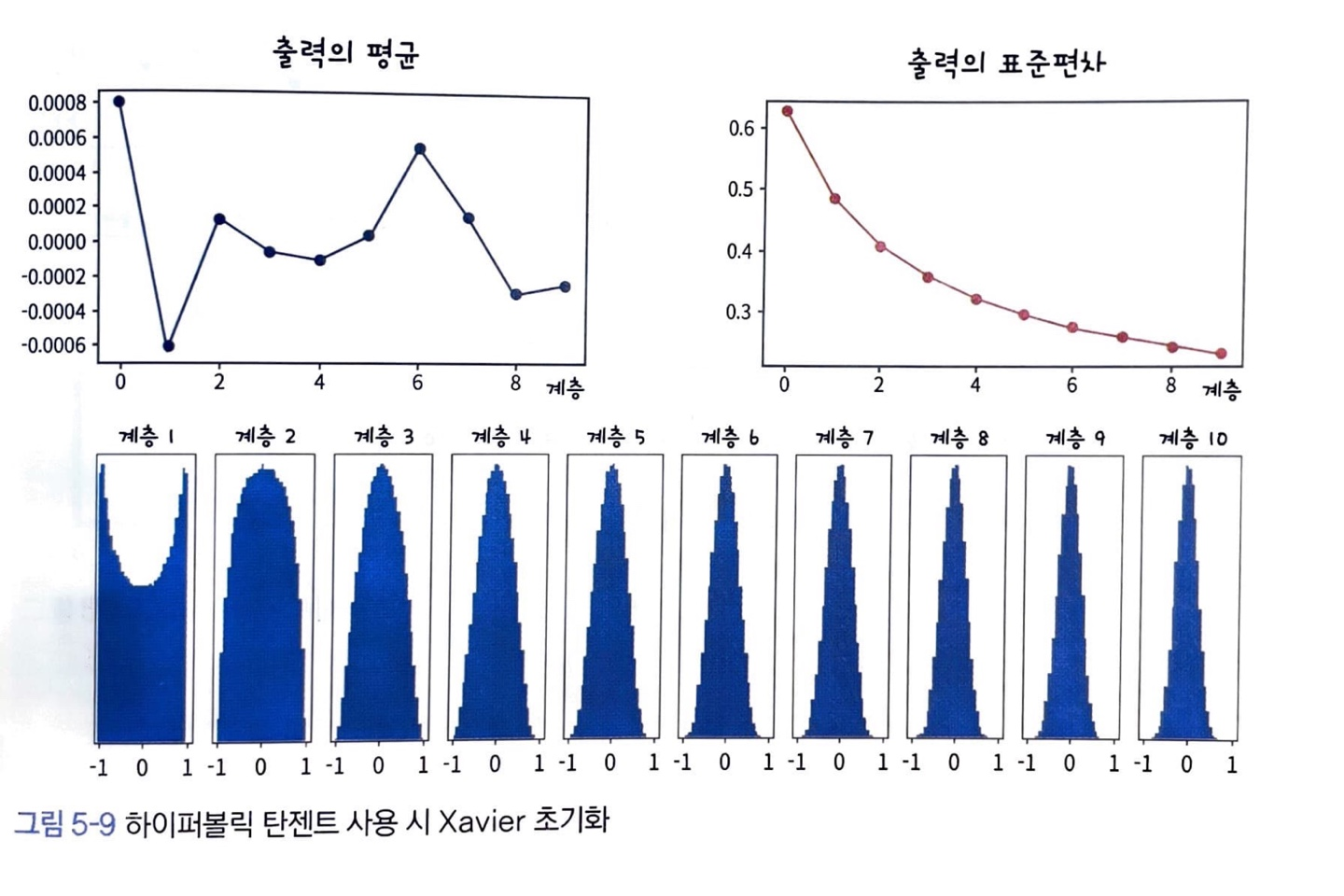
단점: 활성함수가 ReLU일 경우 음수구간에서 0이므로 데이터의 크기가 줄어든다.

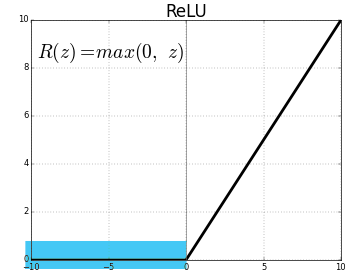
He 초기화

활성화 함수가 ReLU일 때 사용한다.

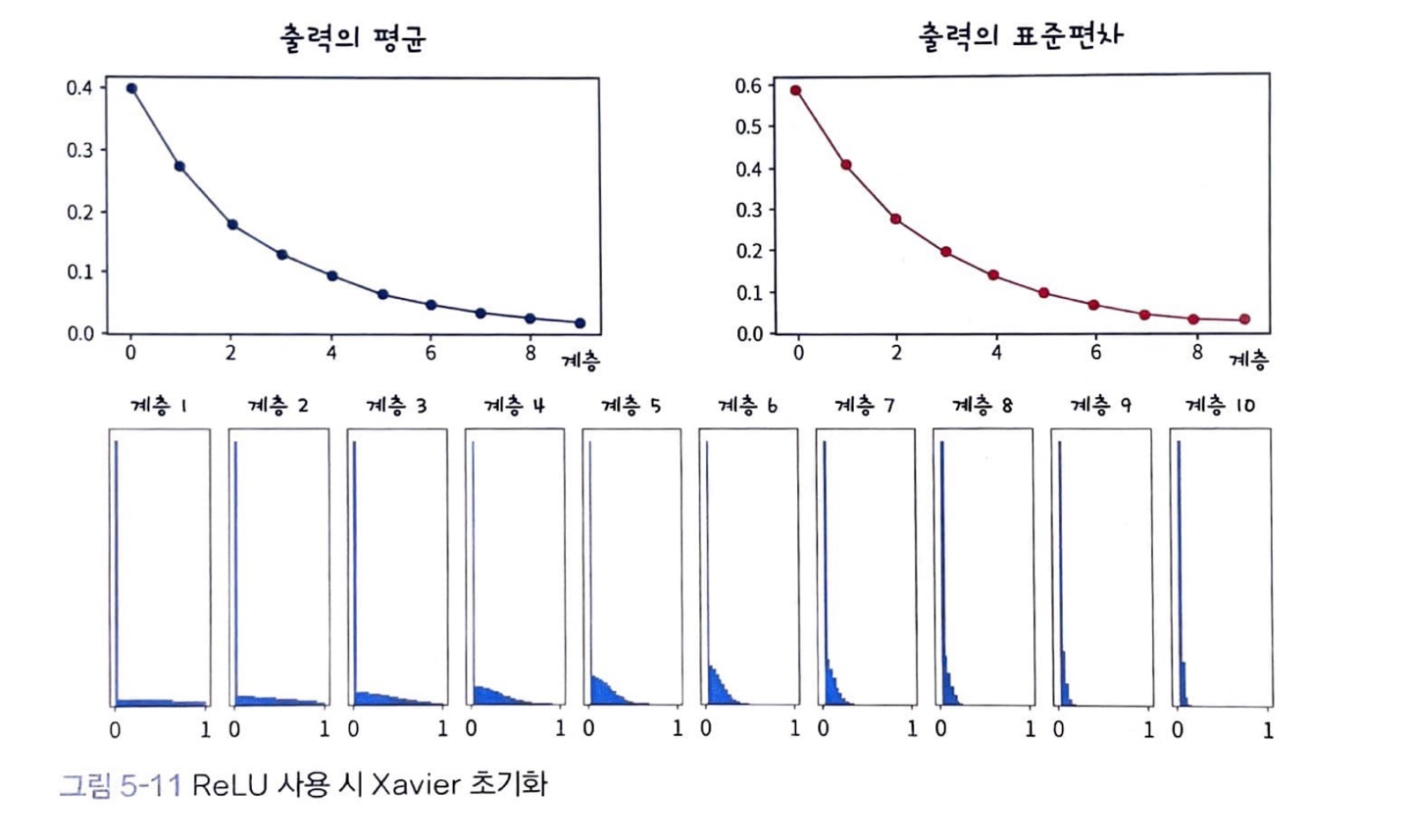
He 초기화는 가중치의 분산을 2/n으로 한다.

간단 정리

• Xavier 초기화
  : sigmoid 계열만 가능
• He 초기화
  : ReLU 가능

참고

• https://velog.io/@cha-suyeon/DL-%EA%B0%80%EC%A4%91%EC%B9%98-%EC%B4%88%EA%B8%B0%ED%99%94Weights-Initialization
• 딥러닝 교과서 (출판사: 이지퍼블리싱)