5-2 정규화(1) BatchNormalization

정규화

• 최적해로 가는 길을 잘 찾을수 있도록 해주는 것
• 최적화 과정에서 최적해를 잘 찾도록 정보를 추가하는 것
• 일반화(generalization)를 잘 하는 모델을 만드는 기법

정규화 접근 방식

• 모델을 최대한 단순하게 만든다.

  • 단순한 모델은 파라미터가 적어서 과적합이 덜 생긴다.

    ex) 필요한 가중치만 남기고, 불필요한 가중치는 0으로 만들면 과적합 방지 가능 => L1 정규화가 여기에 속한다.

• 사전 지식을 표현해서 최적해를 빠르게 찾는다.

  • 사전 지식을 표현하는 방법은 다양하다.
    그 중 하나의 예가 데이터나 모델에 대한 사전분포를 이용해서 정확하고 빠르게 해를 찾는 방법이다.
    ex) 가중치 감소(weight decay)
    

• 확률적 성질을 추가한다
  데이터 또는 모델, 훈련 기법 등에 확률 성질을 부여하여 조금씩 변화된 형태로 데이터를 처리함으로써 다양한 상황에서 학습하는 효과를 줄 수 있다.
  ex) 데이터 증강, dropout ...

• 여러 가설을 고려한 예측
  ensemble, bagging
  

배치 정규화

신경망 학습이 어려운 이유 중 하나는 layer를 지날 때마다 데이터 분포가 보이지 않는 요인에 의해 조금씩 왜곡되기 때문이다.

내부 공변량 변화 (Internal Covariate Shift)

일반적으로 standardization의 목적은 평균으로 구한 분포의 표준 편차를 1로 맞추기 위해 데이터를 바꾸는 것을 의미한다.

이 때, 분포를 결정하는 보이지 않는 요인을 내부 공변량이라 하며, 배치 정규화는 layer를 지날 때 마다 매번 정규화를 한다.

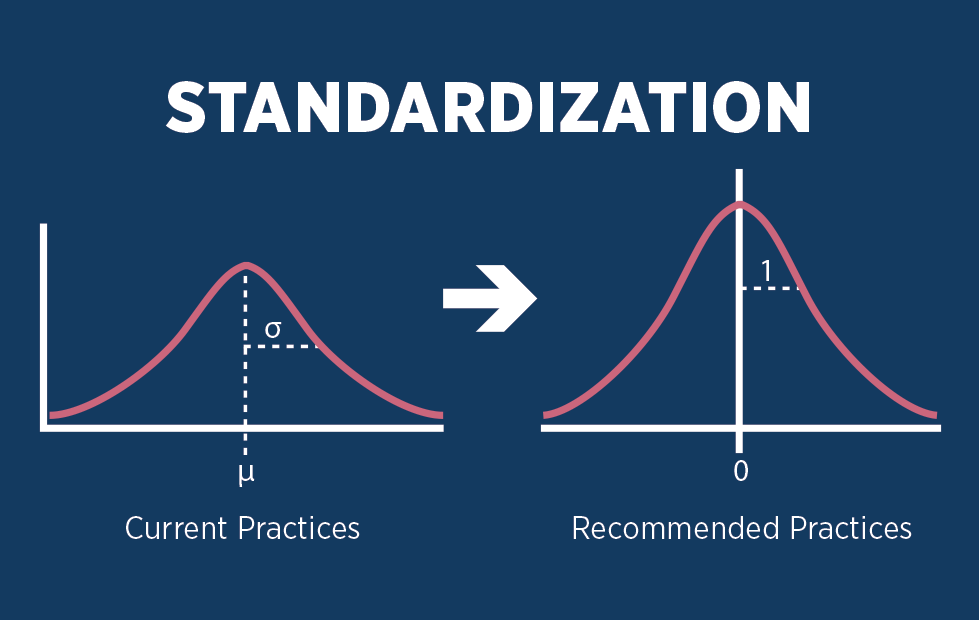
표준 가우시안 분포로 정규화하면아무래도 넓게 퍼져있을 수 있는 데이터($\sigma$)를 $\mathcal{N}(0,1)$로 만듦으로 데이터의 크기가 작아지면서 Internal Covariate Shift도 작게 만들수 있다.

Standardization Normalization Batch 정규화의 문제점

활성 함수를 지날 때 비선형 함수 표현이 사라진다.

표준 정규분포로 데이터는 0근처에 많이 몰리게 되는데 sigmoid 계열의 활성화함수를 거치게 되면 선형 함수구간에 데이터가 몰리게 되고 이는 선형 구간으로 표현될 수 있기 때문에, 비선형 함수로써의 표현 의미가 사라지게 된다.

또한 ReLU를 사용할 경우 데이터의 절반이 날아갈 수 있다.

데이터 분포 원상 복구

그래서 표준 가우시안 분포로 정규화하고 원래 데이터의 분포로 복구해야 한다.

$\hat{x}^k$: 정규화된 데이터
$\beta^k$: 원래 데이터의 평균
$\gamma^k$: 원래 데이터의 표준편차

가우시안 분포

복구 식

가우시안 분포로 나온 식에다가 원래 데이터의 표준편차를 곱하고 평균을 더해주는 역순 과정을 통해 원래 분포로 복구해준다.

$\beta^k$,$\gamma^k$는 학습과정 중 따로 구해야 한다.

최종 식