손실 함수

손실 함수를 정의하는 기준

신경망 모델이 정확하게 예측하려면 모델은 관측 데이터를 잘 설명하는 함수를 표현해야 한다.
이때 모델이 표현하는 함수의 형태를 결정하는 것이 바로 손실 함수이다. 따라서 손실 함수는 모델이 관측 데이터를 잘 표현하도록 정의되어야 한다.

손실 함수가 '최적해가 관측 데이터를 잘 설명할 수 있는 함수의 파라미터값이 되도록' 하려면 어떤 기준으로 정의해야 할까?
1) 모델이 오차 최소화
2) 모델이 추정하는 관측 데이터의 확률이 최대화되도록 최대우도추정
방식으로 정의하는 방법이 있다.

오차 최소화 관점

모델의 오차는 모델의 예측과 관측 데이터의 타깃의 차이를 의미한다.
따라서 손실 함수를 정의할 때 어떤 방식으로 오차의 크기를 측정할지만 정하면 된다. ex) MSE, MAE ...

오차 최소화 관점에서 손실함수를 정의하다보면 $L_2$노름과 $L_1$노름이 나오는데

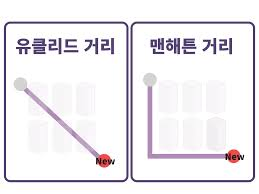
• $L_2$노름 = 유클리드 거리
  두 점 사이의 가장 짧은 거리

• $L_1$노름 = 맨하탄 거리
  각 축을 직각으로 이동하는 거리
  

최대우도추정 관점

우도(likelihood)는 모델이 추정하는 관측 데이터의 확률을 의미한다.
손실 함수의 목표는 관측 데이터의 확률이 최대화되는 확률분포 함수를 모델이 표현하도록 만드는 것이다.

이 방식은 확률 모델인 경우에만 적용할 수 있으면 최대우도추정(MLE)라 한다.

대부분의 신경망 모델은 확률 모델을 가정하므로 MLE로 손실 함수를 유도할 수 있다.

두 방식손실 함수를 정의하는 관점은 다르지만, 손실 함수를 유도해 보면 동일한 최적해를 갖는 함수가 된다.

• 우도 $p(\mathfrak{D}|\theta)$
  학습데이터 $\mathfrak{D} =\{(x_i,t_i):i=1, ...,N\}$의 각 샘플 $(x_i,t_i)$는 같은 분포에서 독립적으로 샘플링된다 할 때, 신경망 모델로 추정한 관측 데이터의 확률

  우도: 파라미터 $\theta$로 추정된 확률 분포에서 관측 데이터 $x$의 확률
  $\mathfrak{L}(\theta|x) = p(x|\theta)$

$p(t_i|x_t;\theta)$: $\theta$라는 파라미터로 이루어진 input $x_t$가 주어졌을 때, $t_i$가 될 확률을 의미한다.

샘플 $(x_i, t_i)$가 서로 독립이므로 관측 데이터의 우도는 N개의 샘플의 우도의 곱으로 표현할 수 있다.

이를 기반으로 MLE는 다음과 같이 표현할 수 있다.

MLE의 최적화 문제 개선

앞에서 정의한 MLE를 조금만 변형하면 수치적으로 다루기 쉬워질 뿐만 아니라, 안정적으로 최적화할 수 있기 떄문에 두 단계를 거쳐 문제를 재정의한다.

1. 우도 대신 log 우도를 사용한다
2. 최대화 문제를 최소화 문제로 변환하기 위해 목적 함수에 음의 log 우도(negative log likelihood)를 사용한다.

• log 적용

  $J(\theta) = log\ p(\mathfrak{D}|\theta) = log\prod_{i=1}^N p(t_i|x_t;\theta)=\sum_{i=1}^Nlogp(t_i|x_t;\theta)$

  log를 사용하는 이유:
  1. 가우시안 분포 또는 베르누이 분포와 같은 지수함수 형태로 표현되는 확률분포의 경우, 로그를 취하면 지수항이 상쇄되어 다항식으로 변환되기 때문에 함수 형태가 다루기 쉬워진다.$\\$
  2. N개 샘플에 대한 우도의 곱을 로그 우도의 합산으로 바꾸면 언더플로를 방지할 수 있다. 확률은 1보다 작기 때문에 확률을 N번 곱하면 N이 커질수록 언더플로가 쉽게 생긴다. 따라서 우도 대신 로그 우도를 사용하면 곱이 합산 형태로 바뀌므로 언더플로를 방지할 수 있다. $\\$
  3. 우도 대신 로그 우도를 사용해도 최적해는 달라지지 않는다.

  • 언더플로란?
    산술 오버플로와 반대되는 개념으로서 산술연산의 결과가 취급할 수 있는 수의 범위 보다 작아지는 상태를 말한다

• 최대화 문제를 최소화 문제로 변환
  로그 우도에 음수를 취한 음의 로그 우도, 즉 NLL(Negative Log Likelihood)로 손실 함수를 정의

  $NLL(\theta) = -log\ p(\mathfrak{D}|\theta) = -log\sum_{i=1}^N p(t_i|x_t;\theta)$

최종 MLE