9장(2) VAE(1)

VAE

오토인코더

오토 인코더를공부하기 전에 표현학습(Representaion Learning)에 대해 잠깐 알아보자

Representation Learning이란?
=> 데이터를 가장 잘 표현하는 특징을 학습하는 방법을 의미한다. 즉, 인코딩을 통한 저차원 공간의 데이터로 압축을 얼마나 잘 하는가를 학습하는 것이 목적이며, 훈련 데이터로부터 응용에 필요한 변동성 요인을 특징으로 얼마나 잘 포착하는가? 를 중점으로 한다.

오토인코더 자체는 학습했던 데이터만 복원할 수 있는 모델이기 때문에 새로운 데이터를 생성할 수는 없다. 이를 확률 모델로 확장(VAE)하면 추정된 확률분포에서 새로운 데이터를 확보할 수 있으며, 이를 통해 새로운 데이터를 생성할 수 있다.

오토 인코더

• encoder에 x를 입력 -> z출력
• decoder에 z를 입력 -> x출력

VAE

• encoder에 x를 입력 -> $p(z|x)$를 출력
• decoder에 z를 입력 -> $p(x|z)$를 출력

실제 데이터의 확률분포는 가우시안 분포보다 훨씬 복잡하다.
-> 확률분포 $p(x)$가 복잡하다면 여러개의 분포가 혼합된 형태의 혼합 분포로 추정할 수 있다.

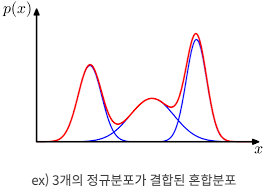
파란선은 각각의 가우시안 분포 $p(x|z_1),p(x|z_2),p(x|z_3)$이며 빨간선은 이를 혼합한 분포이다.

이 때, $p(z)$는 혼합 계수로, 세 가우시안 분포의 발생확률을 의미한다.

가우시안 혼합 분포는 가우시안 컴포넌트 $p(x|z)$를 혼합 계수 $p(z)$로 가중합산한 형태이다.

결합확률 분포, 주변확률 분포

잠깐 위에 나오는 결합확률 분포와, 주변확률 분포에 대해 짚고 넘어가자.

결합확률 밀도함수
두 개의 연속확률 변수 x,y가 존재할 때
1. 모든 (x,y)에 대해 f(x,y)>=0
2. $\int\int f(x,y)dydx=1$
3. $p[(x,y)\in A] = \int\int_Af(x,y)dy,dx$
를 만족하는 f(x,y)를 결합 밀도함수라고 한다.

=> 결합확률 분포는 결합 밀도함수의 연속형 버전이라고 생각하면 된다.

주변확률 분포
주변확률 분포는 결합확률 분포를 전제로 한다.

ex) 3개의 검은구슬, 2개의 붉은구슬, 3개의 흰 구슬이 있다.
임의로 2개의 구슬을 뽑는다면 검은구슬X, 붉은구슬Y개의 결합 확률분포
$A = {(x,y) | x+y <= 1}$일 때, $P[(x,y) \in A]$

각각의 공을 뽑을 수 있는 경우의 수
X=0,1,2 Y=0,1,2 X+Y<=2
-> (0,0), (0,1), (0,2), (1,0), (1,1), (2,0)
f(0,0) = $_3C_2 \over {_8C_2}$ = $3 \over {28}$
f(0,1) = $_2C_1 * _3C_1 \over {_8C_2}$ = $6 \over {28}$
$\vdots$

$A=\{(x,y) | x+y <=1\}$이므로 $P[(x,y) \in A] = f(0,0) + f(0,1) + f(1,0) = {9\over{14}}$

이산확률의 경우

• $f_X(x) = \sum_yf(x,y)$
• $f_Y(y) = \sum_xf(x,y)$

연속확률의 경우

• $f_X(x) = \int_ {-\infin}^{\infin} f(x,y)$
• $f_Y(y) = \int_ {-\infin}^{\infin} f(x,y)$
  $\begin{vmatrix} y/x & 0 & 1 & 2 & f_Y(y)\\ \\ 0 & 3\over{28} & 9\over{28} & 3\over{28} & 15\over{28} \\ \\ 1 & 6\over{28} & 6\over{28} & 0 & 12\over{28} \\ \\ 2 & 1\over{28} & 0 & 0 & 1\over{28} \\ \\ f_X(x) & 10\over{28} & 15\over{28} & 3\over{28} & 1 \\ \end{vmatrix}$

colum = x에 대한 주변확률 분포