9장(2) VAE(2)

이전 글에서는 가우시안 혼합 분포를 알기 위한 기본적인 개념을 알아봤다.

이제부턴 혼합 분포를 기반으로 VAE 모델 아키텍처까지 가기위한 기본적인 개념들을 알아보자.

가우시안 무한 혼합 신경망, 몬테카를로 추정

가우시안 분포가 셀 수 있을 때는 $\sum$으로 처리하면 되지만 혼합 분포가 셀수 없이 많을 때는 $\int$로 처리해줘야 한다.

가우시안 무한 혼합 신경망은 다음과 같다. (나중에 사진 ㄱ)

$p_\theta(x|z) = N(\mu_\theta(z), \sigma^2_\theta(z))$

위의 식을 쓰기 위해선 적분 안쪽이 신경망으로 구성되기 때문에 $z$를 무한히 샘플해야하지만, 실제로는 불가능하기 때문에 몬테카를로 추정 방식을 사용한다.

적분식을 기댓값 형태로 변환 뒤, N번 무작위 샘플링해서 평균을 취한다.

$z \sim p(z)$의미 : "$z$라는 변수가 $p(z)$분포를 따른다"

확률분포 추정

$x = \{x_1, x_2, ..., x_N\}$ (관측데이터)
$z = \{z_1, z_2, ..., z_N\}$ (관측데이터에 대응되는 잠재변수)

최대우도 추정을 위한 최적화 문제정의
확률 $p(x)$를 최대우도 추정 방식으로 추정하자.

모델이 예측한 확률분포 $p_\theta(X)$는 N개의 sample의 우도 $p_\theta(x_i)$의 곱이다.

$p_\theta(X) = \prod_{i=1}^N p_\theta(x_i)$
log 우도 = $p_\theta(X)$ = $log\prod_{i=1}^N p_\theta(x_i) = \sum_{i=1}^N logp_\theta(x_i)$

따라서 최대우도 추정을 위한 최적화 문제는 다음과 같이 정의된다.

잠재변수 모델로 확장

$p_\theta(x_i)$는 복잡한 확률분포이기 떄문에 가우시안 무한 혼한 분포로 정의된다고 가정한다.
단 $p(z_i)$는 사전확률분포이므로 파라미터 $\theta$와 관련이 없다고 가정한다.

앞의 최적화 문제에 $p_\theta(x_i)$를 대입하면 최적화 문제는 다음과 같이 확장된다.

$p(z_i)$는 가우시안 분포로 가정하고 $p(z_i)$에서 $p_\theta(x_i|z_i)$를 추정할 떄는 신경망 모델을 사용하며, 적분식은 기댓값 형태로 변환해서 몬테카를로 추정을 한다.

잠재공간의 분화를 위한 사후분포 사용

위 식으로 훈련하면, $z_i$는 사전 분포로만 정의되고, $x_i$를 표현하도록 정의된 상태가 아니기 때문에 $p_\theta(X)$의 분포를 따르는 데이터를 생성할 수 없다.
즉, 사전 분포로 정의된 $z_i$가 있는 잠재 공간은 데이터의 특징을 반영하지 않은 상태이다.

$z_i$가 $x_i$를 잘 표현하려면 $x_i$에서 $z_i$를 구해서 잠재 공간이 $z_i$별로 잘 분화되도록 해야한다. (-> 이게 제일 뭔 소린가 싶었음)

잠재 공간이 잘 분화되도록 사후 분포 $p_\theta(z_i|x_i)$를 구해서 사전 분포 $p(z_i)$대신 적용하면 최적화 문제가 다음과 같이 재정의된다

사후 확률분포의 변분 근사

그런데 사후 분포 $p(z_i|x_i)$는 매우 복잡한 분포이기 때문에 추정하기 어렵다.

이와 같이 확률분포를 추정하기 어려운 경우 $q_\theta(z_i|x_i)$함수로 근사할 수 있으며 이를 변분 근사(variable approximation), 변분 추론(variable inference)이라고 한다.

$q_\theta(z_i|x_i)$는 변분 함수이며, 간단한 가우시안 분포를 기반으로 사후 분포를 근사하게끔 도와주는 함수이다.

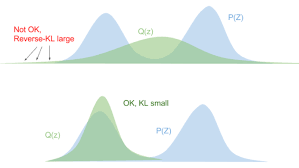
(사진은 그냥 참고용으로 q가 가우시안 분포를 따른다는 것만 알고 넘어가자)