Loss Function
이전 강의에서 봤던 Linear Classification에서, 파라미터 중 W값을 임의로 설정하여 진행하였다.
하지만 score의 개선을 위해 더 적절한 W값을 구해야 하고, 이 과정에서 쓰이는 것이 Loss Function이다.
우리는 Loss Function을 최소화 시키는 파라미터를 찾아야 한다.
Multiclass SVM loss
Loss Function의 한 종류이다.

그림과 같은 방법으로 데이터마다 Loss를 계산한다.

그렇게 나온 Loss에 대해 평균을 내면 dataset에 대한 전체적인 Loss가 나온다.
- car의 score가 조금만 변한다면?
- loss min/max 값은?
- W값이 너무 작아서 모든 score가 거의 0일 때 loss는?
- j = y_i인 경우도 sum에 포함시킨다면?
- 총합이 아닌 평균을 쓴다면?
- 손실을 제곱하여 더한다면?
1) loss는 변하지 않는다. 이미 car의 score가 다른 class 보다 높기 때문이다.
2) 0에서 무한대이다.
3) 손실은 대략 (Class의 개수) - 1 로 맞춰진다.
4) 완벽하게 분류를 해도 loss는 1이 된다.
5) 스케일만 변할 뿐 결과는 같다.
6) loss가 nonlinear하게 된다.
plus. Loss가 0이 되는 W를 찾았다고 할 때, 이 W는 유일한가?
ans) 아니다. 2W, 3W, ... 모두 Loss는 0이다.
Regularization
Training data에 대한 성능은 굉장히 중요하진 않다.
우리는 처음보는 test data에도 잘 작동하게 모델을 만들어야 하고, 이때 중요한 것이 regularization이다.
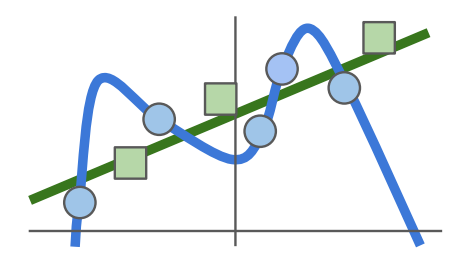
Regularization은 위 그림과 같이 model이 training data에 너무 과하게 맞춰지는 것(overfitting)을 막는다.

Regularization에도 여러 종류가 있는데, 가장 흔히 쓰이는 것은 L2이다.
Softmax
또 다른 loss function엔 softmax가 있다.
딥러닝에서 더 흔히 쓰이는 방법이다.
SVM과 Softmax의 차이를 간단히 말하면 SVM은 정답 클래스와 오답 클래스의 score 차이를 중요하게 생각하고, Softmax는 각각의 score 자체를 해석하고자 한다.

softmax는 위와 같은 절차로 지수화, normalize, -log를 취한다.
loss는 0에서 무한대 범위까지 나올 수 있다.
그렇다면 loss를 최소화하는 W는 어떻게 찾을까?
Optimization
Optimization은 loss가 최소인 지점을 찾는 과정이라고 할 수 있다.
Optimization에도 여러 방법이 있다.
Random search
Random search는 랜덤으로 W를 많이 설정해보고 loss를 계산해보는 방법인데, 성능이 좋지 않아서 실제로는 쓰지 않는다.
Gradient
두번째는 gradient를 이용하는 방법이다.
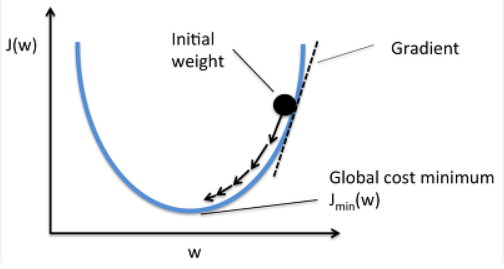
현재 위치의 변화율(gradient)를 구한 후, gradient의 반대방향으로 W를 조금씩 조정하면 loss의 값을 줄일 수 있다.
Numerical gradient

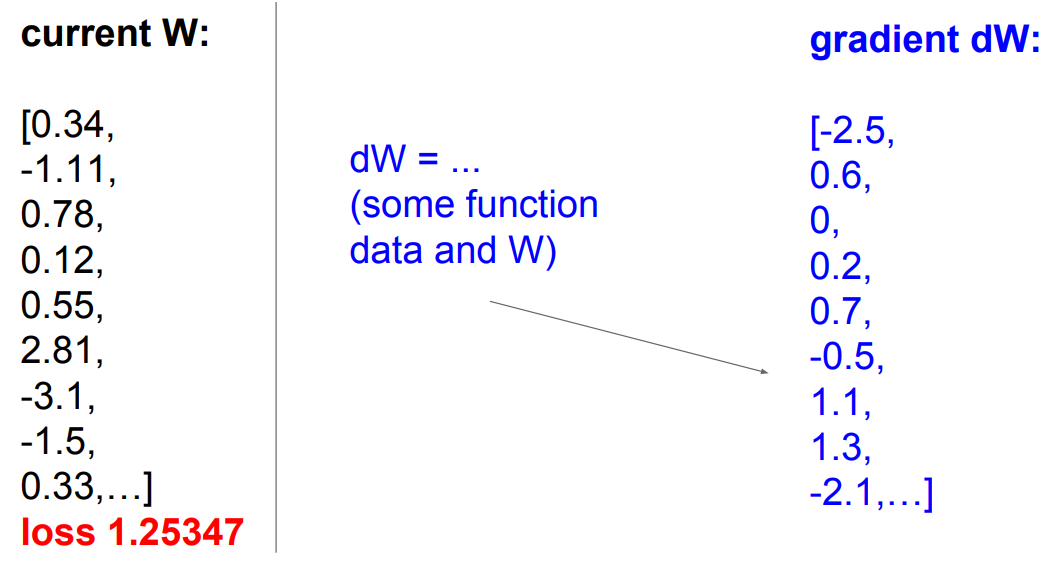
그림과 같이 W를 미세하게 증가시킨 후 계산하면 loss는 줄었고 기울기는 -2.5였다.
이런 식으로 하나씩 계산시키는게 numerical gradient인데, 이것은 너무 느려서 효율적이지 않다.
Analytic gradient
다행히도 이미 만들어져 있는 미분식을 이용하면 더 정확하게, 더 빠르게 계산할 수 있다.
Gradient descent

우리가 공부한 Gradient descent를 코드로 나타낸 것이다.
Gradient descent는 W를 초기에 설정하고 W를 계속 업데이트해가는 방식이다.
그림에서 step_size(learning rate)는 hyperparameter이다. 미리 정해야 한다.
실제로 dataset의 크기는 매우 클 수 있으므로, 위와 같은 방식으로는 parameters를 업데이트 할 때마다 모든 dataset을 사용해야 하므로 computing적인 측면에서 비효율적이다.
SGD
이때 사용하는 것이 SGD(Stochastic Gradient Descent)이다.

매번 전체 training dataset에 대해 계산하지 않고, minibatch(32,64,128)을 이용해 loss를 계산하고 parameter를 업데이트한다.
