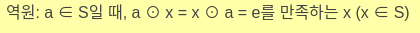항등원과 역원

조건

1. 연산에 대하여 닫혀 있어야 한다.
2. 교환 법칙이 성립해야 한다.

항등원

집합 S의 임의의 원소 a와 원소 e를 연산한 결과가 a가 될 때 e를 연산에 대한 항등원 이라고 함.

10 + 0 = 10 --> 덧셈에 대한 항등원 0

10 x 1 = 10 --> 곱셈에 대한 항등원 1

역원

집합 S의 임의의 원소 a와 x를 연산한 결과가 항등원 e가 될 떄 x를 연산에 대한 a의 역원 이라고 함.

항등원이 나오게 하는 수

10 + -10 = 0 --> 10의 덧셈에 대한 역원 -10

10 x 1/10 --> 10의 곱셈에 대한 역원 1/10