📝 문제 설명
트리에서 리프 노드란, 자식의 개수가 0인 노드를 말한다.
트리가 주어졌을 때, 노드 하나를 지울 것이다.
그 때, 남은 트리에서 리프 노드의 개수를 구하는 프로그램을 작성하시오.
노드를 지우면 그 노드와 노드의 모든 자손이 트리에서 제거된다.
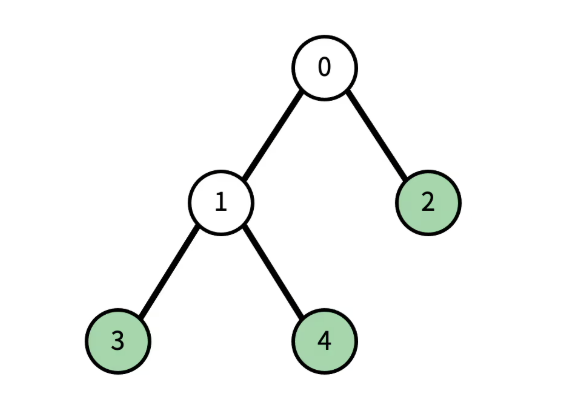 현재 리프 노드의 개수는 3개이다. (초록색 색칠된 노드) 이때, 1번을 지우면, 다음과 같이 변한다. 검정색으로 색칠된 노드가 트리에서 제거된 노드이다.
현재 리프 노드의 개수는 3개이다. (초록색 색칠된 노드) 이때, 1번을 지우면, 다음과 같이 변한다. 검정색으로 색칠된 노드가 트리에서 제거된 노드이다.
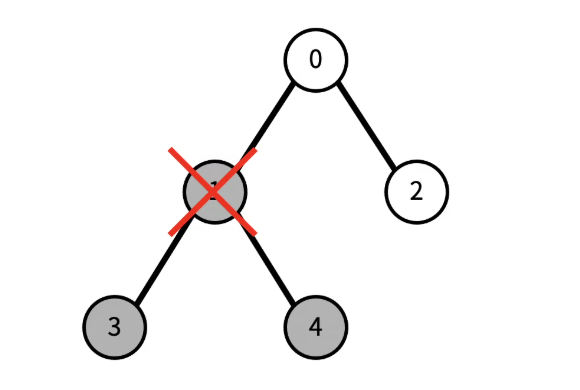 이제 리프 노드의 개수는 1개이다.
이제 리프 노드의 개수는 1개이다.
입력
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다. 셋째 줄에는 지울 노드의 번호가 주어진다.
출력
첫째 줄에 입력으로 주어진 트리에서 입력으로 주어진 노드를 지웠을 때, 리프 노드의 개수를 출력한다.
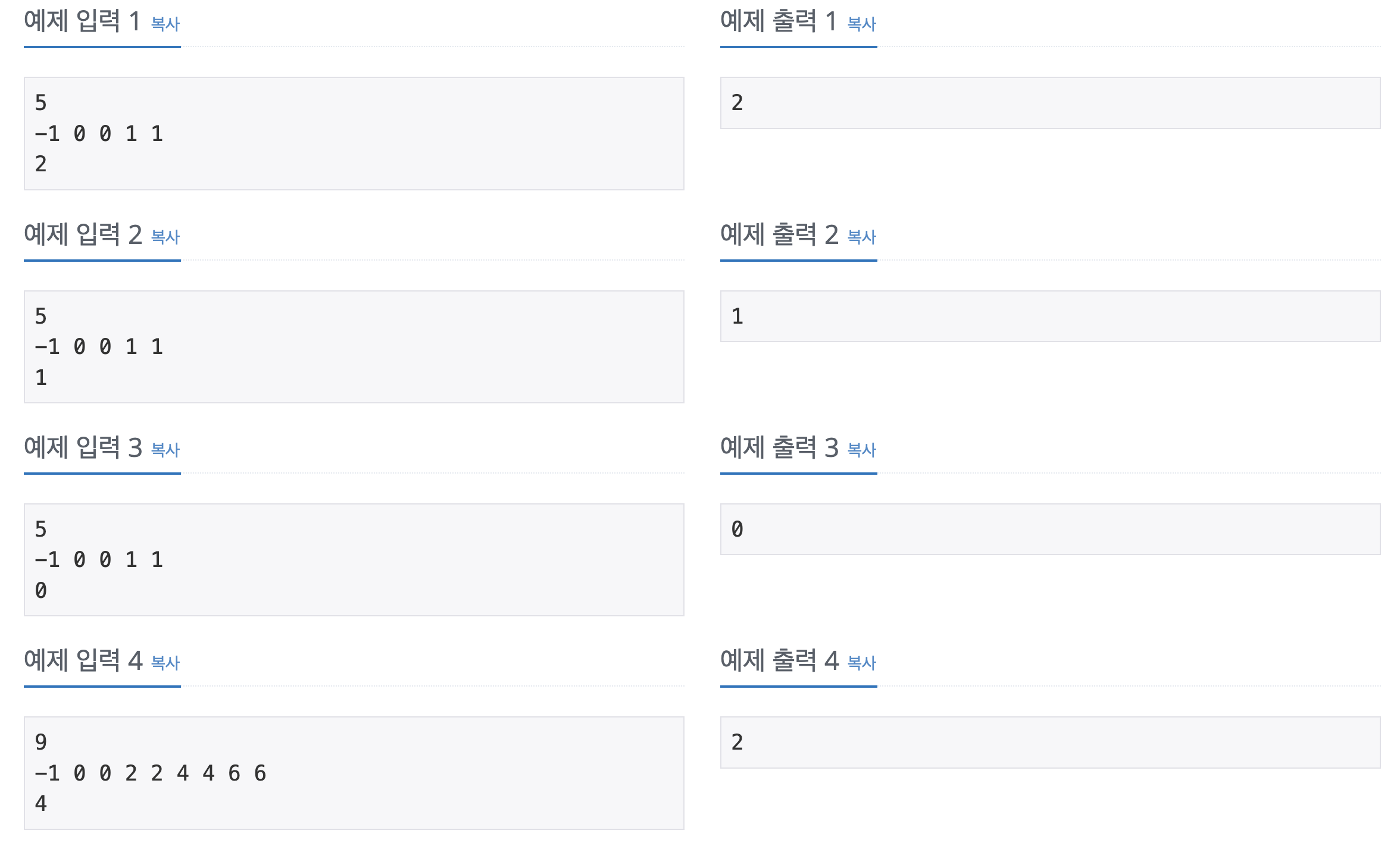
입출력 예시
문제 들여다 보기.. 👀
위 문제는 트리의 구조를 ArrayList 배열로 표현하고, 특정 노드를 제거한 후 남은 트리에서 리프 노드의 개수를 계산하는 프로그램이다.
1️⃣ 트리 입력 처리
- 각 노드의 부모를 기준으로 트리를 구성
- 즉, 인덱스를 각 노드의 부모로 가정
- 부모가
-1인 경우 해당 노드는 root 에 값 저장 - 트리의 자식 노드를
ArrayList배열로 저장
n = 5; // n은 노드의 개수
// ArrayList 빈 배열값으로 tree 초기화 해주기
tree = new ArrayList[n];
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
// 두 번째 줄인 각 노드의 부모값을 이용해 tree에 저장
// 트리의 인덱스를 각 노드의 부모라고 가정
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < n; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent != -1) {
tree[parent].add(i);
} else {
root = i; // 루트 노드 저장
}
}
tree[parent].add(i) 에서 저장된 값은 [ [1, 2], [3, 4], [ ], [ ], [ ] ] 으로,
- [1, 2]의 부모는 0,
- [3, 4]의 부모는 1를 의미한다.
2️⃣ DFS를 이용한 탐색
- 루트 노드에서 시작하여 스택을 활용해 노드를 탐색할 예정
- 삭제할 노드가 아닌 경우에만 탐색
- 자식 노드가 없는 경우(리프 노드일 경우)에 result를 증가
public static void dfs(int delete) {
Stack<Integer> stack = new Stack<>();
stack.add(root);
if (delete == root) return; // 루트를 삭제하는 경우 처리
while (!stack.isEmpty()) {
int node = stack.pop();
int count = 0; // 자식 노드 개수
for (int child : tree[node]) {
if (child != delete) { // 삭제 노드 제외
stack.add(child);
count++; // 자식 노드가 있음을 나타내는 count
}
}
if (count == 0) result++; // 자식 노드가 없으면 리프 노드이므로 결과값 증가
}
}
📌 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main {
static int n;
static ArrayList<Integer>[] tree;
static int root;
static int remove;
static int result = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
tree = new ArrayList[n];
for (int i = 0; i < n; i++) {
tree[i] = new ArrayList<>();
}
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < n; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent != -1) {
tree[parent].add(i);
} else {
root = i;
}
}
remove = Integer.parseInt(br.readLine());
dfs(remove);
System.out.println(result);
}
public static void dfs(int delete) {
Stack<Integer> stack = new Stack<>();
stack.add(root);
if (delete == root) return;
while (!stack.isEmpty()) {
int node = stack.pop();
int count = 0;
for (int child : tree[node]) {
if (child != delete) {
stack.add(child);
count++;
}
}
if (count == 0) result++;
}
}
}