📝 문제 설명
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때,
각 노드의 부모를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 노드의 개수 N (2 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N-1 개의 줄에 트리 상에서 연결된 두 정점이 주어진다.
출력
첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.
입출력 예시
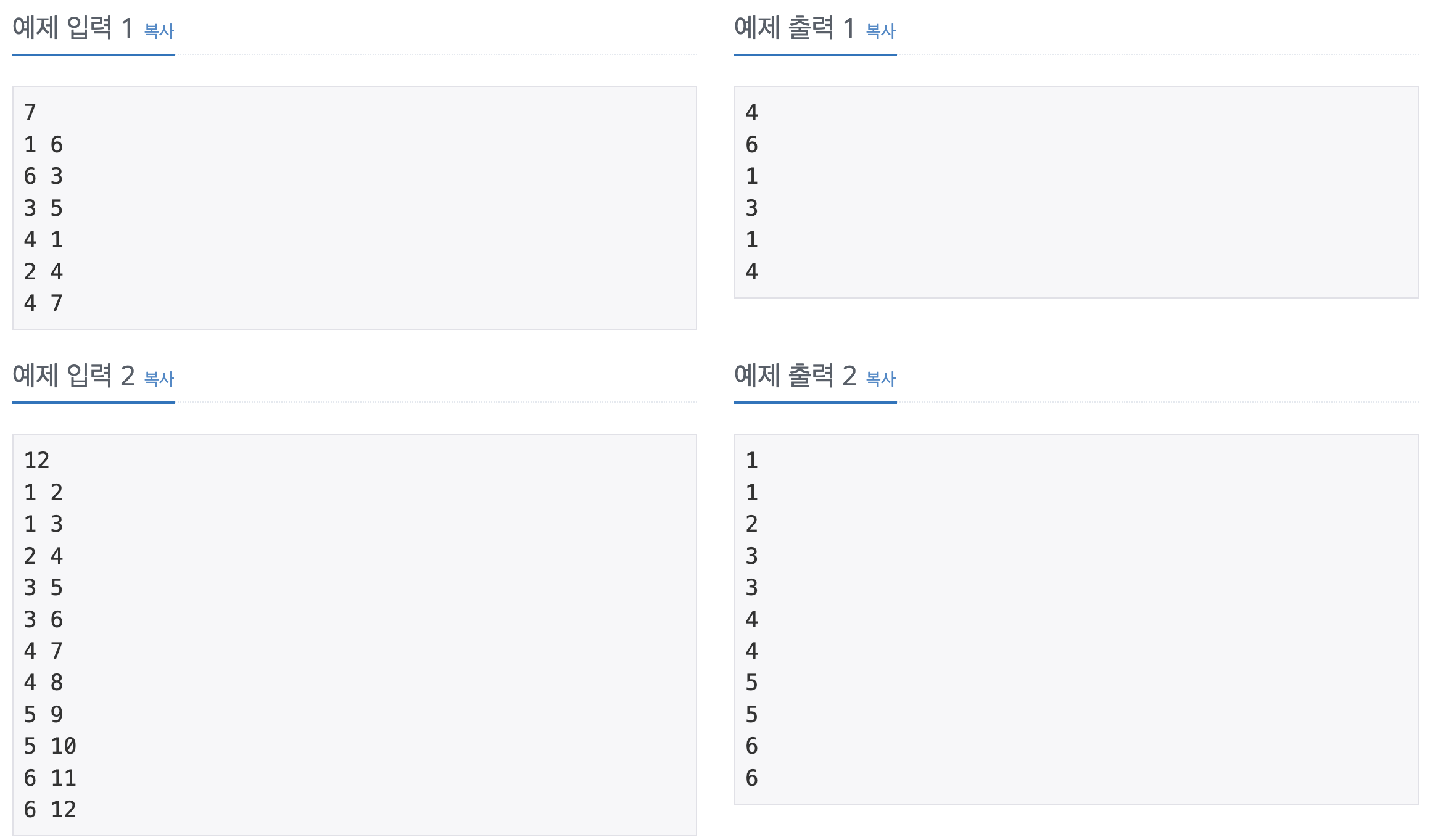
문제 들여다 보기.. 👀
문제에서 잘 봐야할 곳
- Root 는 1
N-1개의 줄- N 노드의 수
문제를 그림으로 나타내보면 아래와 같다.
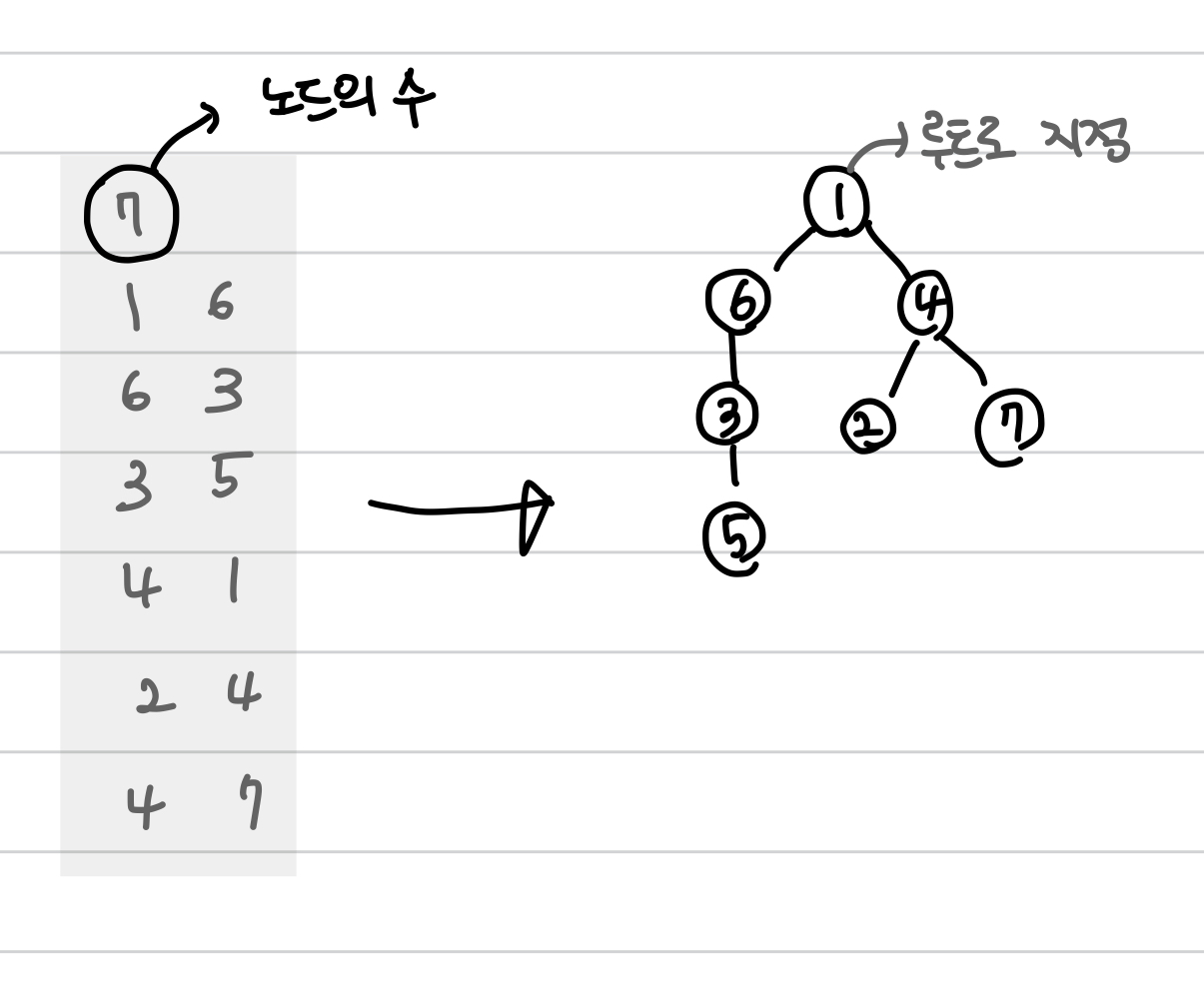
출력
- 첫째 줄부터 N-1개의 줄에 각 노드의 부모 노드 번호를 2번 노드부터 순서대로 출력한다.
2번 노드의 부모 : 4
3번 노드의 부모 : 6
4번 노드의 부모 : 1
...
...
...
풀이
이번 문제는 BFS(Breadth-First Search; 너비 우선 탐색) 을 사용하여 풀 수 있다.
BFS(Breadth-First Search)
시작 노드에서 출발해 시작 노드를 기준으로 가장 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
FIFO 탐색 -> Queue 자료구조를 이용한다.
목표 노드에 도착하는 경로가 여러개일 때 최단경로를 보장한다.
1️⃣ 방문 확인 여부 배열
한번 방문한 노드를 다시 방문하면 안되기 때문에, 노드 방문 여부를 체크할 배열이 필요하다.
// 방문 확인 여부
boolean[] isVisited = new boolean[n + 1];
- n개의 노드를 가진 트리로 배열을 만들어 준다.
(단, 0번 인덱스는 사용하지 않는다. ) - 해당 노드를 방문하면 해당 인덱스의 값을
TRUE로 바꿔준다.
2️⃣ 인접리스트 초기화
각 노드에서 연결된 이웃 노드를 확인 후 인접 리스트 로 초기화 시켜준다.
// 인접 리스트를 담을 배열 생성
List<List<Integer>> tree = new ArrayList<>();
// 0번 인덱스는 사용하지 않고 1번 인덱스부터 시작할 예정
// 총 n+1개의 방 초기화
for (int i = 0; i < n + 1; i++) {
tree.add(new ArrayList<>());
}
// 문제 입력 조건에서 n-1개의 줄이 주어지므로 n-1
for (int i = 0; i < n - 1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int left = Integer.parseInt(st.nextToken());
int right = Integer.parseInt(st.nextToken());
tree.get(left).add(right);
tree.get(right).add(left);
}
- tree 는 다음과 같이 저장된다.
[ [ ], [ 6, 4 ], [ 4 ] , [ 6, 5 ], [ 1, 2, 7 ] , [ 3 ] , [ 1, 3 ], [ 4 ] ]
3️⃣ Queue에서 노드를 꺼낸 후 방문하지 않은 인접노드를 Queue에 삽입
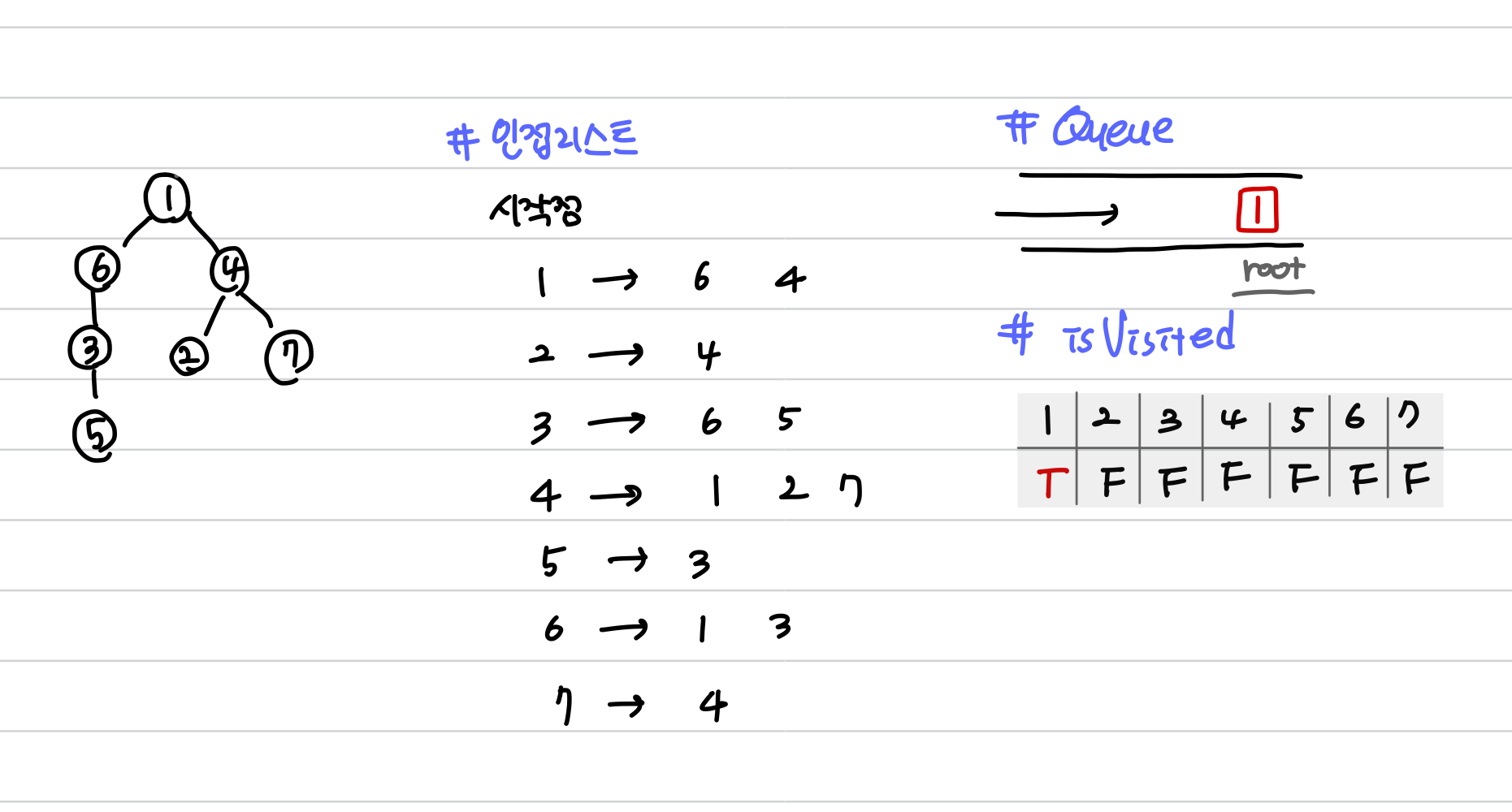
// 시작점(루트)을 1로 지정
isVisited[1] = true;
Queue<Integer> queue = new LinkedList<>();
queue.add(1);
- 시작점(루트)을 1로 정했기 때문에 시작점의 방문배열을 ture로 바꿔준다.
- queue에 시작점을 add 해준다.
...
...
int node = queue.poll(); // 노드 꺼내기
int child = tree.get(node); // 1의 인접한 노드 구하기
for (int child : tree.get(node)) {
// 인접 노드를 방문하지 않았다면
if (!isVisited[child]) {
isVisited[child] = true; // 방문 표시
parent[child] = node; // 부모 노드 저장
queue.add(child); // queue 에 삽입
}
}
..
..- 처음에 넣었던 노드 1을 Queue에서 꺼낸다.
- tree 에서 꺼낸 노드
1의 인접 노드를 찾는다. - 찾은 노드는 방문 했으므로
true로 변경 - queue 에서 꺼낸 1의 인접 노드인 child를 queue에 삽입한다.
- queue가 비어있을때까지 반복
⭐️ 부모 노드 ⭐️

여기서 인접리스트의 4 를 보면 인접한 노드는 1, 2, 7 로 총 3개이다.
이때 1은 방문된 노드(true)로 처리되었으며 이는 4의 부모 노드임을 의미한다.
이는 BFS(또는 DFS) 탐색 중, 현재 노드의 인접 노드들 중 이미 방문된 노드는 항상 부모 노드로 간주되기 때문이다.
따라서, queue에서 꺼낸 노드의 인접한 노드 중, 이미 방문한 노드는 해당 인접한 노드의 부모이므로 배열에 따로 저장해준다.
📌 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine()); //노드의 개수
List<List<Integer>> tree = new ArrayList<>(); // 트리 선언
// 1번 인덱스부터 시작할 예정, 총 8개의 방 필요하므로 n+1
for (int i = 0; i < n + 1; i++) {
tree.add(new ArrayList<>());
}
// 문제 입력 조건에서 n-1개의 줄이 주어지므로 n-1
for (int i = 0; i < n - 1; i++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int left = Integer.parseInt(st.nextToken());
int right = Integer.parseInt(st.nextToken());
tree.get(left).add(right);
tree.get(right).add(left);
}
// queue 사용 및 기본 설정
int[] parent = new int[n + 1];
boolean[] isVisited = new boolean[n + 1];
Queue<Integer> queue = new LinkedList<>();
queue.add(1); // root = 1 지정 (문제 조건)
isVisited[1] = true;
// 비어 있을 때까지 반복
while (!queue.isEmpty()) {
int node = queue.poll();
for (int child : tree.get(node)) {
if (!isVisited[child]) {
isVisited[child] = true;
parent[child] = node;
queue.add(child);
}
}
}
// 2부터 출력
for (int i = 2; i <= n; i++) {
System.out.println(parent[i]);
}
}
}