[백준] #1967번 트리의 지름 1 (Java)

백준 1967 - 트리의 지름 바로가기

📝 문제 설명

트리(tree)는 사이클이 없는 무방향 그래프이다.
트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다.
트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다.
이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.

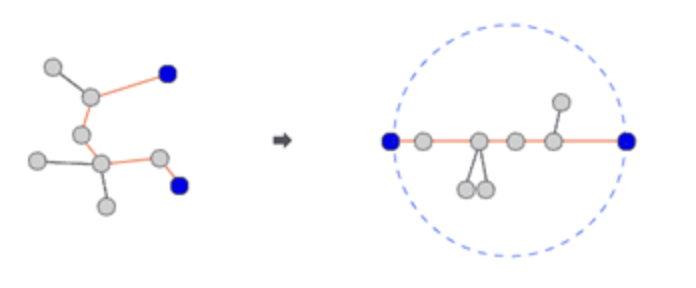
이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다.
정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.

입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 
아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.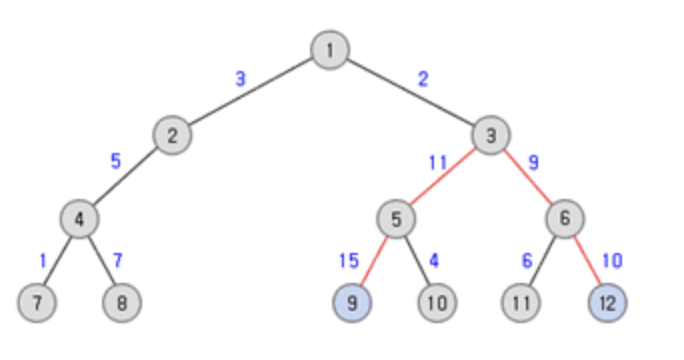

---

입력
파일의 첫 번째 줄은 노드의 개수 n (1 ≤ n ≤ 10,000) 이다.
둘째 줄부터 n-1 개의 줄에 각 간선에 대한 정보가 들어온다.
간선에 대한 정보는 세 개의 정수로 이루어져 있다.

• 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호
• 두 번째 정수는 자식 노드
• 세 번째 정수는 간선의 가중치

간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.

출력
첫째 줄에 트리의 지름을 출력한다.

입출력 예시

---

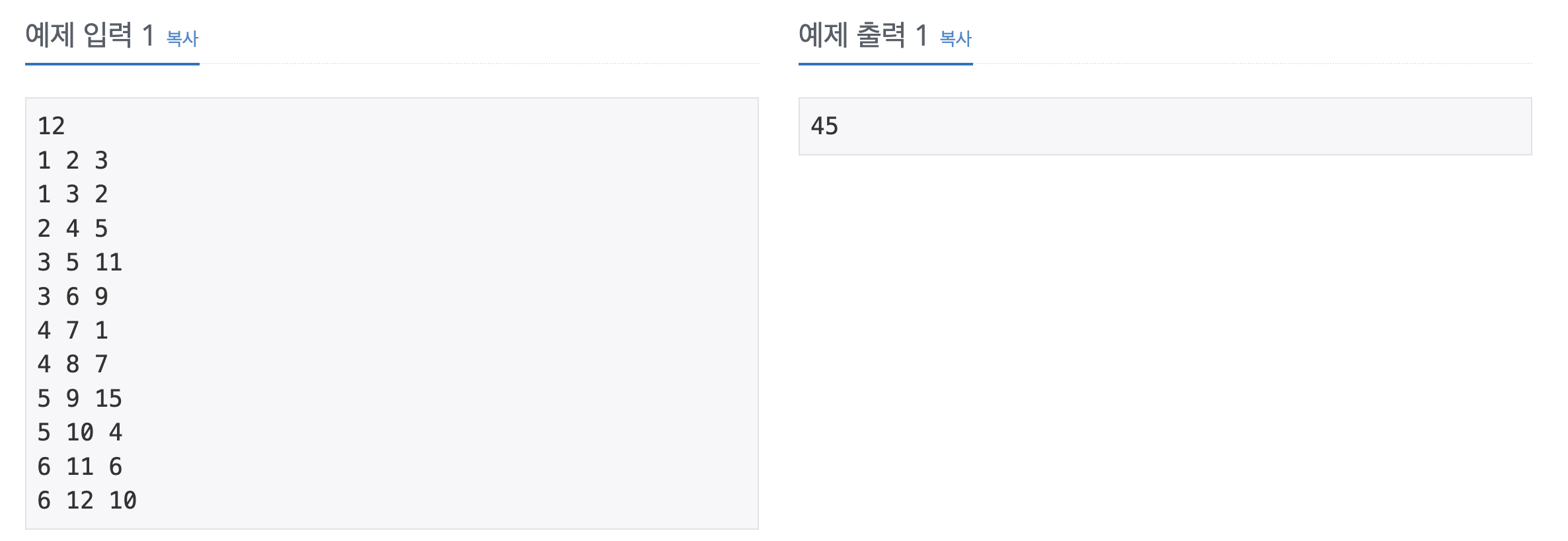
문제 들여다 보기.. 👀

두 번의 DFS

오늘의 키포인트는 DFS(깊이 우선 탐색) 를 두 번 실행하는 것이다.

왜 두 번의 DFS를 사용할까?

1. 첫 번째 DFS : 임의의 노드에서 시작

트리의 임의의 노드(보통 1번 노드)에서 시작한다고 가정했을 때, 이 DFS의 목적은 트리의 지름 끝점 중 하나를 찾는 것이다.

트리의 특성상 한쪽 끝에서 다른 끝으로 가장 먼 거리를 탐색하면 지름의 한쪽 끝점에 도달한다는 뜻이다.

즉, 첫 번째 DFS 는 가장 먼 노드 farthestNode 를 구할 수 있다.
이 노드는 지름을 이루는 두 끝점 중 하나이다.

2. 두 번째 DFS

첫 번째 DFS에서 찾은 끝점 farthestNode 을 시작점으로 다시 DFS를 실행한다.

이 두 번째 DFS는 farthestNode 에서 가장 먼 노드까지의 거리를 구한다.

이 거리가 바로 트리의 지름이다!!

---

코드 구현

1️⃣ 트리 입력 처리

public class Main {
	static int n; // 노드의 개수
    static ArrayList<Node>[] tree; // 트리의 인접리스트
    static boolean[] visited; // 방문 체크 배열
    static int maxDistance = 0; // 트리의 지름
    static int farthestNode = 0; // 가장 먼 노드
    
    ...



	// 트리 초기화
	tree = new ArrayList[n + 1];
	for (int i = 1; i <= n; i++) {
		tree[i] = new ArrayList<>();
	}

• tree 배열은 각 노드와 연결된 간선을 저장하는 인접 리스트이다.
• 크기는 n+1 로 선언해 1번부터 n번 노드를 처리

	// 입력 처리
	for (int i = 0; i < n - 1; i++) {
		StringTokenizer st = new StringTokenizer(br.readLine());
		int parent = Integer.parseInt(st.nextToken());
		int child = Integer.parseInt(st.nextToken());
		int weight = Integer.parseInt(st.nextToken());

		// 양방향 간선 추가
		tree[parent].add(new Node(child, weight));
		tree[child].add(new Node(parent, weight)); 
     }

tree[parent].add(Node) 와 tree[child].add(Node) 에서 저장된 메모리 구조를 살펴보면

tree[1] => [Node(2,3), Node(3,2)]
tree[2] => [Node(4, 5)]....
...
...

로 트리의 인접리스트를 확인할 수 있다.

2️⃣ DFS를 이용한 탐색

// 예외 처리 (노드가 1개일 경우)
if (n == 1) {
	System.out.println(0);
	return;
}

• 예외 처리로 노드가 1개일 경우 return 값 설정

// 첫 번째 dfs
visited = new boolean[n + 1];
dfs(1, 0);

• 첫 번째 dfs 는 임의 노드 1에서 시작하여 가장 먼 노드를 탐색할 예정

// 두 번째 dfs
visited = new boolean[n + 1]; // 방문 체크 배열 초기화
maxDistance = 0; // 트리의 지름 초기화
dfs(farthestNode, 0);

• 두 번째 dfs 는 첫 번째 dfs 에서 찾은 노드에서 시작하여 가장 먼 노드를 탐색할 예정

// DFS 함수
static void dfs(int currentNode, int distance) {
	visited[currentNode] = true;

	// 최대 거리 갱신
	if (distance > maxDistance) {
		maxDistance = distance;
		farthestNode = currentNode; // 가장 먼 노드 저장
	}

	// 연결된 노드 탐색
	for (Node next : tree[currentNode]) {
		if (!visited[next.node]) {
			dfs(next.node, distance + next.weight);
		}
	}
}

---

📌 전체 코드

package com.example.testcodeinjava;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Main {
    static int n; // 노드의 개수
    static ArrayList<Node>[] tree; // 트리의 인접리스트
    static boolean[] visited; // 방문 체크 배열
    static int maxDistance = 0; // 트리의 지름
    static int farthestNode = 0; // 가장 먼 노드

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());

        // 예외 처리: 노드가 1개인 경우
        if (n == 1) {
            System.out.println(0);
            return;
        }

        // 트리 초기화
        tree = new ArrayList[n + 1];
        for (int i = 1; i <= n; i++) {
            tree[i] = new ArrayList<>();
        }

        // 입력 처리
        for (int i = 0; i < n - 1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());

            int parent = Integer.parseInt(st.nextToken());
            int child = Integer.parseInt(st.nextToken());
            int weight = Integer.parseInt(st.nextToken());

            // 양방향 간선 추가
            tree[parent].add(new Node(child, weight));
            tree[child].add(new Node(parent, weight));
        }

        // 임의의 노드(1번)에서 가장 먼 노드 찾기
        visited = new boolean[n + 1];
        dfs(1, 0);

        // 가장 먼 노드에서 dfs 실행
        visited = new boolean[n + 1];
        maxDistance = 0; // 트리 지름 초기화
        dfs(farthestNode, 0);

        System.out.println(maxDistance);

    }

    static void dfs(int currentNode, int distance) {
        visited[currentNode] = true;

        // 최대 거리 갱신
        if (distance > maxDistance) {
            maxDistance = distance;
            farthestNode = currentNode;
        }

        // 현재 노드와 연결된 모든 노드 탐색
        for (Node next : tree[currentNode]) {
            if (!visited[next.node]) {
                dfs(next.node, distance + next.weight);
            }
        }
    }

    static class Node {
        private int node;
        private int weight;

        public Node(int node, int weight) {
            this.node = node;
            this.weight = weight;
        }
    }
}