오차행렬, MAE, MSE, RMSE, R2-Score의 이해

Jihyun·2023년 10월 23일

AI 모델링을 진행할 때 흔히 Train data와 Validation data로 분할한다. train data를 통해 모델을 학습시키고 validation data로 성능을 검증하는 것이 일반적인 방법이다. 그렇다면, 성능을 적절하게 평가하는 기준을 알아야 최선의 모델을 선택할 수 있지 않을까? 지도학습의 회귀(Regression)와 분류(Classificaion)에 대해 알아보자

1. 분류 모델 평가하기

1) 오차 행렬(Confusion Matrix)

오차 행렬은 classification을 평가할 때 가장 널리 쓰이는 지표다. 이름처럼 개념을 혼동하는 경우가 많은데 경우를 나눠서 잘 이해하는 것이 중요하다.

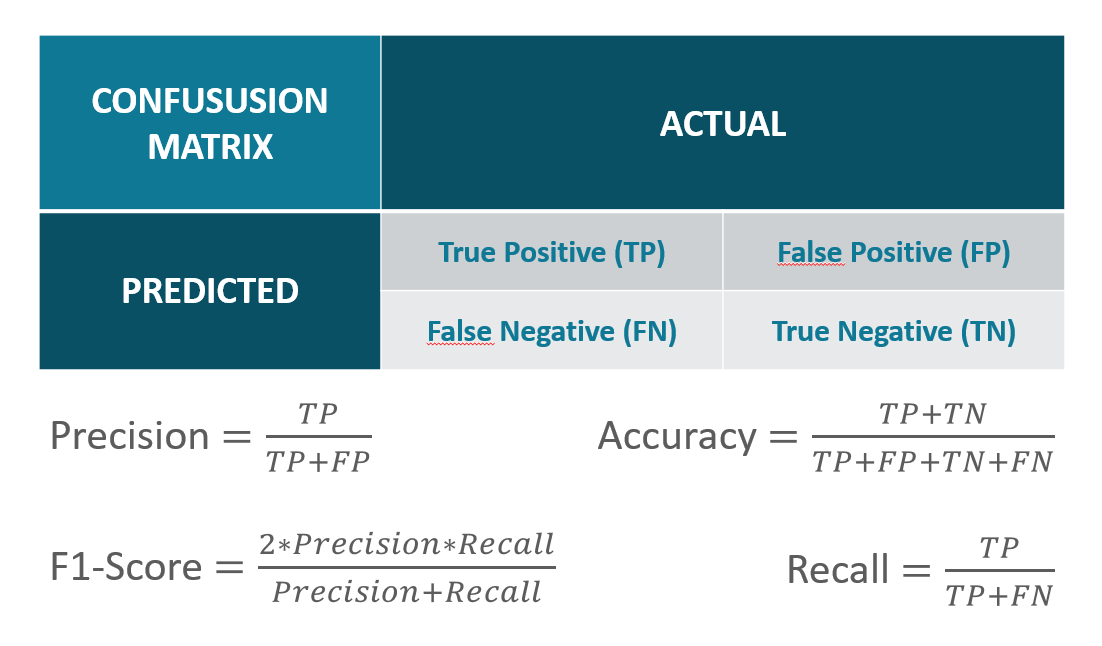
오차행렬이 가지는 각 block의 의미

TP(True Positive) : 실제 답이 positive이고, 예측값도 positive로 정답

FP(False Positive) : 실제 답이 Negative인데, 예측값이 Positive로 오류

FN(False Negative) : 실제 답이 Positive인데, 예측값이 Negative로 오류

TN(True Negative) : 실제 답이 Negative이고, 예측값도 Negative로 정답

전체데이터 = TP + FP + FN + TN

오차행렬 평가지표의 의미

Accuracy(정확도) : 전체 데이터 중 예측하여 맞춘 값의 비율 $(TP+TN)\over(TP+FP+FN+TN)$

Recall(재현율) : 실제값이 Potivie인 것 중 예측값이 Positive인 비율 $TP\over(TP+FN)$

Precision(정밀도) : Positive로 예측한 것 중 실제값이 Positive인 비율 $TP\over(TP+FP)$

F1-score : Recall과 Precision의 조화평균 $2\times Recall\times Precision \over Racall+Precision$

분류 모델을 평가하는 4가지 지표를 알아봤다. 이때 주의할 점은 어느 하나의 지표만을 가지고 모델 성능을 평가하는 것은 매우 어려운 것이기에 예측 하고자 하는 데이터에 따라 정밀도가 중요할 수도, 재현율이 더 중요할 수도 있기 때문에 적절히 사용해야 한다. 다만, 일반적으로 재현율과 정밀도는 trade-off 관계(한 쪽이 높아지면 다른 한 쪽이 낮아지는 현상)이기 때문에 2가지 지표를 모두 고려해야한다. F1-score가 두 가지 지표를 모두 고려한 것이다.

정확도 vs F1-score

만약 데이터가 균등하게 나뉘어져 있다면(ex. 7:3), 정확도와 F1-score 모두 사용 가능하다. 단, 데이터가 편중(Imbalanced)되어 있는 경우에는 정확도의 성능이 떨어진다. 이를 '정확도의 함정'이라고도 한다. F1-score는 각 레이블당 재현율과 정밀도가 각각 계산되고 이를 활용하여 종합적인 지표를 제공하기 때문에 데이터가 편중되어 있는 경우에는 정확도 보다 F1-score를 사용하는 것이 더욱 효과적이다.

2) ROC vs AUC

- ROC

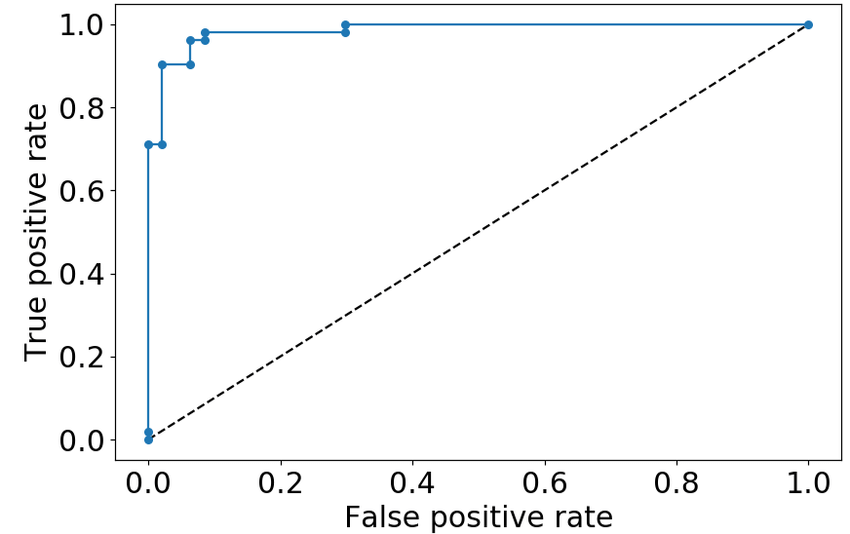
ROC(Receiver Operation Curve)는 FPR(False Positive Rate)이 변함에 따른 TPR(True Positive Rate)의 변화를 그린 곡선이다. FPR은 $FP\over(TN+FP)$ 로 실제 Negative 중 Positive라고 잘못 예측한 비율을 의미하므로 낮을수록 좋다. TPR은 $TP\over(TP+FN)$ 로 실제 Positive 중 Positive라고 잘 예측한 비율을 의미하므로 높을수록 좋다. 곡선이 직각에 가까울수록 모델의 성능이 좋다고 판단한다. 반대로 Random(직선)에 가까울수록 성능이 나쁘다고 판단한다. Random은 무작위로 예측했을 때 나올 수 있는 최솟값을 선으로 나타낸 것이다.

- AUC

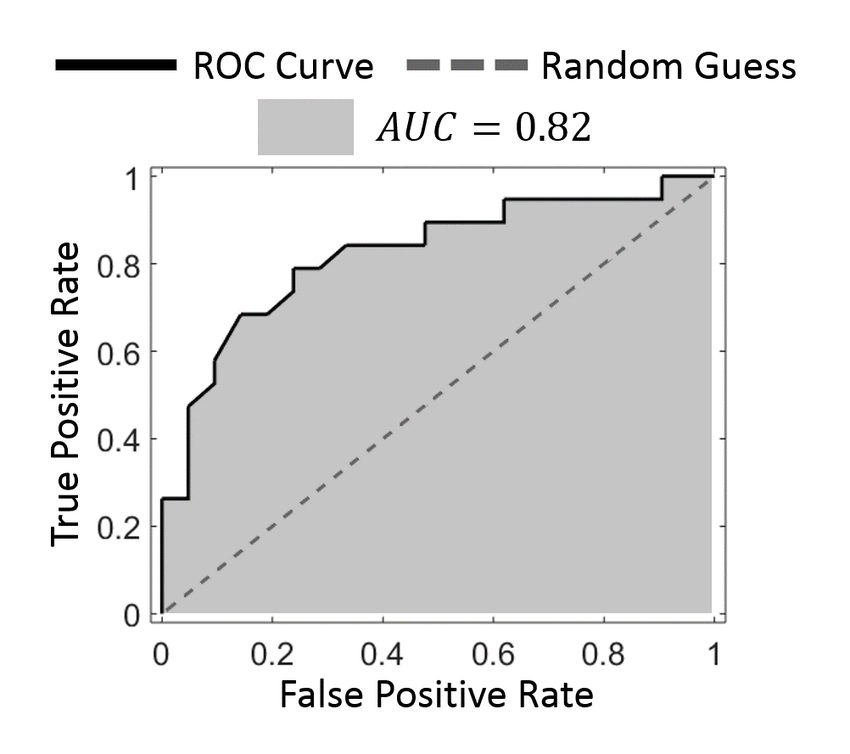
AUC(Area Under ROC)는 ROC 곡선 아래의 면적을 의미한다. AUC값이 클수록 모델의 성능이 좋다고 판단한다. 최댓값은 1이고 최솟값은 0.5다.

2. 회귀 모델 평가하기

1) MAE

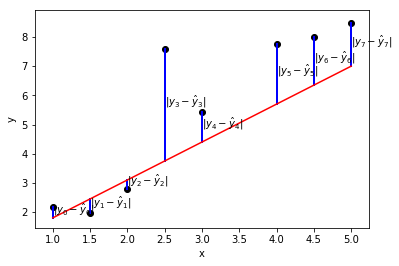
MAE(Mean Absoulte Error, 평균절대오차)의 식은 다음과 같다.

$MAE$ = $\sum|y-\hat y|\over n$

$y$ = 실제값 $\hat y$ = 예측값 $n$ = 데이터 수
예측값에 대한 실제값의 오차를 구하고 그 절댓값의 평균을 구하는 방식이다.

MAE로 모델을 평가할 때는 오차가 작을수록 모델의 성능이 좋은 것이므로 MAE가 작을수록 모델의 성능이 좋다고 판단하면 된다.

2) MSE

MSE(Mean Squared Error, 평균제곱오차)의 식은 다음과 같다.

$MSE$ = $\sum(y-\hat y)^2\over n$

$y$ = 실제값 $\hat y$ = 예측값 $n$ = 데이터 수
예측값에 대한 실제값의 오차를 구하고 그 제곱값의 평균을 구하는 방식이다.
절댓값을 취하는 것(MAE)와 제곱을 취하는 것(MSE)의 차이는 이상치와 같은 특이값의 영향도를 파악하는 데에 있다. MSE는 특이값이 발생했을 때 오차를 제곱하기 때문에 수치가 크게 늘어난다는 특징이 있다. 그렇기에 MSE는 데이터분석을 할 때 손실함수(Cost Fucntion)로 자주 사용된다.

MAE vs MSE

MAE는 일반적인 회귀지표로 사용되고, MSE는 손실함수로 사용된다.

3) RMSE

RMSE(Root Mean Squared Error, 평균 제곱근 오차)의 식은 다음과 같다.

$RMSE$ = $\sqrt{\sum(y-\hat y)^2\over n}$

$y$ = 실제값 $\hat y$ = 예측값 $n$ = 데이터 수
RMSE는 MSE에 루트를 취한 지표다. MSE는 데이터가 많고 오차가 커질수록 그 값이 기하급수적으로 커지기 때문에 지표로 활용하기 어려운 경우가 생긴다. 따라서 루트를 씌어 값을 축소한 것이 RMSE다. RMSE는 MAE와 더불어 가장 일반적으로 쓰이는 회귀지표 중 하나다.

4) R2 Score

R2 Score = 결정계수(Coefficient of Determination) = R-Squared
R2 Score는 회귀 모델에서 독립변수가 종속변수를 얼마나 잘 설명해주는 지 나타내는 지표다.

$R^2$ = $1-$ $\sum(t-y)^2\over \sum(t-\bar t)^2$ = $1-$ $\sum(오차)^2\over \sum(편차)^2$

$t$ = 실제값 $y$ = 예측값 $\bar t$ = 평균값

R2 Score <= 0: 쓰레기 모델, 모델 활용 불가

0 < R2 Score < 1 : 1에 가까울 수록 좋은 모델

R2 Score = 1 : 가장 좋은 모델
결정계수가 높다는 것은 독립변수가 종속변수를 잘 나타낸다는 의미인데, 독립변수의 개수가 늘어나면 결정계수도 함께 증가한다. 그러므로 독립변수가 2개 이상일 경우에는 조정된 결정계수(Adjusted R-Squared)를 사용해줘야 한다.