머신러닝의 지도학습(Supervised Leanring)에는 회귀(Regression)과 분류(Classification)의 개념이 존재한다. 회귀는 연속적인 수치형 데이터를 예측하는 모델이고, 분류는 'Y or N', '사과 or 포도'처럼 범주형 데이터를 분류하는 모델이다. 오늘은 가장 기초적인 회귀 모델인 선형 회귀에 대해 알아보도록 하자.

선형 회귀는 데이터의 관계를 가장 잘 나타내는 추세선(Trendline)을 예측하는 모델이다. 추세선이란 시계열 데이터를 분석할 때 자주 보이는데, 데이터의 추세를 그래프로 표현하여 패턴을 예측하는 데에 사용된다. 우리는 선형회귀를 사용하여 feature(X)와 label(Y)의 관계를 가장 잘 설명하는 모델을 만들 수 있다. 선형회귀는 우리가 중학교 때 배웠던 1차 함수의 형태와 유사하다. 'y=ax+b'의 형태인데 선형성을 가지기 때문에 기울기(coef)와 절편(intercept)를 가지고 모델이 설명하고자 하는 방향을 파악할 수 있다.
임의의 데이터를 생성하여 선형회귀 알고리즘의 원리를 파악해보자.

선형회귀 원리 파악하기

선형회귀는 사이킷런(sckit-learn) 라이브러리를 활용할 수 있다. 필요한 라이브러리를 불러오고 y=2x+9라는 임의의 데이터를 생성해보자.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# X = 1~10, Y=2X+9 학습 데이터 생성
x = []
y = []
for i in range(1,11):
    x.append(i)
    y.append(2*i+9)

print('x =',  x)
print('y =', y)

result:
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [11, 13, 15, 17, 19, 21, 23, 25, 27, 29]

# 선형회귀 학습하기
# 선형회귀 생성
reg = LinearRegression()

x = np.array(x).reshape(-1,1)

print('x:', x)
print('x.shape:', x.shape)

# 선형회귀 학습
reg.fit(x,y)

# coef, intercept 확인
print('coef : ', reg.coef_)
print('intercept : ', reg.intercept_)

# coef와 intercept로 수동 계산하여 비교값 생성하기
coef_intercept = x*reg.coef_[0] + reg.intercept_
print('result', coef_intercept)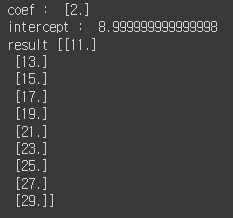

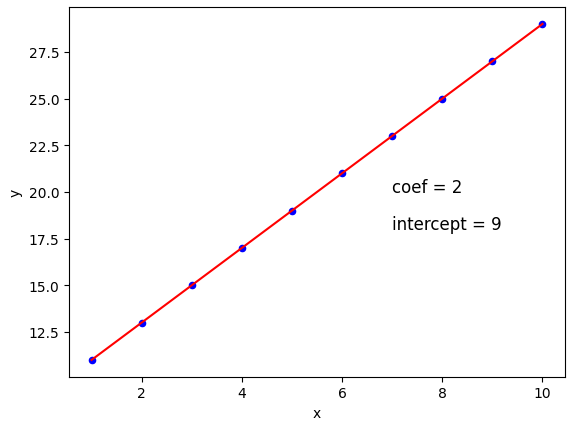
coef는 2, intercept는 9가 나온 것을 확인할 수 있다. 앞서 설정한 y=2x+9와 비교해 봤을 때 학습이 잘 된 것이다.

# 결과비교
# scatter plot 생성
plt.scatter(x,y,color='b', s=20)

# line plot
plt.plot(x, coef_intercept, color='r')

# coef 값 그래프 내에 삽입
plt.text(7, 20, 'coef = %.0f'%reg.coef_[0], size=12)

# intercept 값 그래프 내에 삽입
plt.text(7, 18, 'intercept = %.0f'%reg.intercept_, size=12)

plt.xlabel('x')
plt.ylabel('y')
plt.show()