데브코스 46일차 - 머신러닝 (개념, 선형대수, 확률)

키워드

머신러닝, 선형대수, 확률

머신러닝 기초 개념

• 머신러닝이란?

  • 데이터에서 지식을 추출. 머신 스스로가 데이터의 특징과 패턴을 찾아냄
  • 명시적 프로그래밍의 한계를 극복할 수 있는 기법

• 인공지능: (단순히) 기계가 사람의 지적 능력을 모방하는 것

  • 어떻게 할 것이냐? → 학습을 통해 예측을 진행 (머신러닝)
  • 어떻게 학습할거냐? → 사람의 인지과정을 모방 (딥러닝)

• 명시적 프로그램

  • 규칙 기반(rule-based) 전문가 시스템
  • 처리과정이 이해가 쉬우며, 작은 데이터에서 효과적
  • 하지만 특정 작업에만 국한되며, 변경에 대응이 어려움, 전문가가 필요

• 머신러닝

  • 데이터 내부에서 자주 발생하는 특징과 패턴을 감지
  • 예상치 못한 상관관계를 파악하는데 탁월함
  • 머신 학습을 위해 다양한 데이터가 필요하며, 결과 분석 과정에서 사람이 이해할 수 없는 포인트가 존재할 수 있음 (블랙박스)
  • 활용 사례
    • 추천, 페이스아이디, 의료 영상 처리, 음성처리, 금융 데이터 예측
  • 프로젝트
    • 문제정의 → 데이터 확인 → 데이터 처리 및 분할 → 알고리즘 탐색(선행 연구 참고) → 데이터 전처리(모델 input의 형태로 변경) → 학습과 검증 → 최종 테스트(데이터 문제, 코드 에러, 새로운 알고리즘) → 시스템 런칭(모니터링, 유지보수)

머신러닝 종류

• 데이터 종류
  • 메타 데이터: 기본 데이터에 추가적으로 제공되는 정보 (대체로 학습에 사용 X), 데이터 출처, 형식, 위치 등
  • 레이블 (타겟): 특정 문제에 해당하는 데이터의 설명 혹은 답변을 의미(데이터가 속할 범주), 회귀 문제라면 데이터가 표현할 특정 숫자
    • 대부분 사람이 직접 생성해줘야하는 경우가 많음
• 지도학습
  • 레이블(정답) 정보를 활용해 알고리즘을 학습하는 학습 방법 → 비교적 쉽고 잘 학습되며 성능을 쉽게 측정할 수 있다.
  • 데이터와 레이블 사이의 관계를 파악
  • 하지만 레이블을 만들어내기 위해 드는 비용이 큼
• 비지도 학습
  • 정답 레이블 정보 없이 입력 데이터만을 활용해 알고리즘을 학습 (데이터 내부에 존재하는 패턴을 스스로 파악)
  • 레이블 준비할 필요 없어 비용적 이점이 있으며 사용자가 의도한 패턴 외의 새로운 패턴을 찾을 가능성이 있음
  • 하지만 성능 측정의 기준이 없어 해석이 주관적일 수 있으며 신뢰할 수 있는 결과를 얻기 위해선 다수의 데이터가 필요
• 준지도 학습
  • 일부의 데이터만 정답이 존재, 다수의 데이터에는 레이블이 없는 상황에서 알고리즘을 학습
  • 레이블링 된 데이터로 특성을 파악하고, 레이블링 되지 않은 데이터로 전체 데이터의 패턴을 파악하는 방식으로 학습이 진행
  • 레이블이 부족한 데이터셋에서 유용하며 많은 데이터를 활용할 수 있으므로 일반화 성능을 향상시킬 수 있음
  • 하지만 품질이 낮은 데이터 존재에 취약할 수 있으며, 알고리즘의 복잡성이 증가
• 자기 지도 학습
  • 정답이 하나도 없는 데이터에서 정답을 강제로 생성 후 학습하는 학습 방법론
  • 데이터를 훼손하고 그 데이터를 예측하도록 함
  • 이렇게 만들어진 알고리즘은 해당 데이터를 이용한 다른 문제에 적용 (pre-training)
  • n회 이상의 추가적인 학습 과정이 필요할 수 있으며 알고리즘이 잘못된 패턴을 학습할 위험이 있음
• 강화학습
  • 어떤 환경(마당)에서 상호작용하는 에이전트(강아지)가 보상(간식)을 통해 특정 행동(앉기)을 하도록 유도하는 학습 방법론 (like 강아지 훈련)

머신러닝에 필요한 선형대수1

• 선형대수: 수 들이 모여있는 개념과 관련된 식을 연구하는 분야 (벡터, 행렬 등)

• 수의 집합

  • 스칼라: 수 하나
  • 벡터: 한 방향(차원)으로 숫자가 모인 형태 (1차원)
  • 행렬: 두 방향(차원)으로 숫자가 모인 형태 (2차원)
  • 텐서: 벡터와 행렬을 일반화한 개념

• 행렬의 덧셈과 뺄셈

  • 같은 크기의 행렬 끼리만 가능 (element-wise operation)

• 행렬의 곱셈

  • 하나의 행렬의 각 행과 다른 행렬의 각 열 간의 내적
  • (mn) (nk) = (mk)
  • 하마다르 프로덕트(element-wise product)가 우리가 아는 곱셈임

• 전치 행렬

  • 행과 열을 바꾼 행렬 (nm → mn)
  • 기존 행렬과 전치 행렬이 같은 경우, 그 행렬을 대칭 행렬이라고 함

• 역행렬

  • 행렬 A에 행렬 B를 곱했을 때 결과가 항등행렬(대각성분이 모두 1, 나머지는 0)이면, B를 A의 역행렬이라고 함 (B = A^(-1))
  • 모든 행렬이 역행렬을 갖는 건 아님. (행렬이 가역이 아닌 경우, det(A)=0 )

• 선형 변환

  • Av = v’ → 어떤 벡터에 특정 행렬을 곱해 새로운 벡터를 만듦. v와 v’는 A행렬에 의해 방향이 바뀌는데 이를 선형 변환이라고 함(벡터의 방향과 크기)
  • Av = λv (v가 크기만 변화) 라고 한다면, 그런 벡터를 고유 벡터라고 하고, 그런 상수를 고유 값이라고 한다.
  • 행렬 A의 고유 벡터 v는 행렬 A의 값이 가장 많이 분산되는(많은 정보를 갖고있는) 방향을 나타냄. 즉 데이터가 담고있는 여러 정보 중 가장 의미가 큰 방향이 고유 벡터가 됨. 분산이 크면 람다(고유값)가 크다.
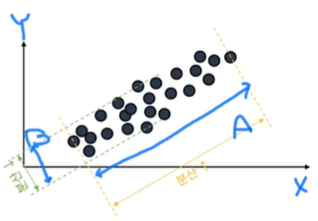
  • 고유 벡터와 고유 값은 복수개가 가능하다. 행렬이 n차원이면 고유 벡터, 고유값도 n개
  • 고유값을 기준으로 나열된 고유벡터는 해석력이 큰 방향의 순서를 의미

특이값 분해 (SVD)

• like 소인수분해…
• 복잡한 행렬 A(m*n)을 더 간단한 세 가지 행렬(U, Σ, V^T)로 분해
  • U의 열벡터들은 A의 왼쪽 특이 벡터로 AA^T(m*m)의 고유 벡터 (행 정보를 바탕으로 중요도를 파악)
  • V의 열벡터들은 A의 오른쪽 특이 벡터로 A^TA(n*n)의 고유 벡터 (열 정보를 바탕으로 중요도를 파악)
  • Σ의 대각선 위의 값들로 A의 특이값 (AA^T와 A^TA의 고유값의 제곱근 값)
• 고유 벡터와 고유값은 행렬 A가 정사각 행렬(m*m)일 경우에만 사용 가능
  • 그렇기 때문에 AA^T와 A^TA가 만들어짐 → 직사각 행렬도 고유벡터, 고유값 분석을 할 수 있게 함

확률 이론

• 확률: 특정 사건이 일어날 가능성을 수치로 표현한 것 (0~1)

• P(x): x라는 사건이 일어날 확률 ⇒ 확률 변수 x가 특정 값을 가질 확률

• 합의 법칙: 두 사건 A, B가 배타적이라면 A또는 B 확률: P(A) + P(B)

• 곱의 법칙: 두 사건 A, B가 독립일 때, A와 B가 동시에 발생할 확률: P(A) * P(B)

• 조건부 확률: 사건 B가 일어난 상태에서 사건 A가 일어날 확률: P(A|B)

• 확률 분포

  • 확률 변수가 취할수 있는 값(x)과 그 값들이 발생하는 확률(y)을 설명하는 개념
  • 이산 확률 분포
    • 확률 변수가 취할 수 있는 값이 개별적이며 셀 수 있는 경우
    • 각 변수에 해당하는 확률 값의 총 합은 1
  • 연속 확률 분포
    • 확률 변수가 연속적인 범위의 값을 취할 수 있는 경우
    • 모든 확률 변수 전 구간의 적분 값은 1
    • ex) 표준 정규 분포 ⇒ 평균이 0, 표준편차가 1

• 확률 변수

  • 실험, 관찰, 또는 무작위 과정의 결과로 나타날 수 있는 수치적인 값
  • 확률 분포로부터 확률 변수를 임의로 생성하는 것을 샘플링이라고 함
  • 특정 분포 D를 따르는 확률 변수 X를 n개 샘플링 하면 X1, X2, … , Xn ~D로 표현 가능

• 확률론적 모델링과 추론

  • 주어진 데이터를 확률 이론의 관점에서 해석하고 모델을 설계하는 과정을 의미
  • 데이터가 특정 확률 분포를 따른다고 가정 (데이터에 존재하는 불확실성을 인지)
  • 머신러닝 모델의 출력은 확률론적 관점에서 예측된 결과물이므로 실제 결과물과 차이가 있을 수 있음
    • 모델의 예측은 y햇으로 표시
  • 입력 데이터는 X로 표시하며, 각 개념(컬럼)은 독립변수이고, 정답이 되는 레이블(y)은 종속변수가 됨

요약 숙제

1. 머신러닝
   1. 머신러닝은 데이터에서 특징과 패턴을 스스로 학습하는 방법을 의미한다. 크게는 인공지능에 속해있으며, 딥러닝을 포함하는 개념이다. 사람이 발견하지 못한 새로운 상관관계를 발견하는 데 용이함. 추천 시스템, 음성 처리 등에 사용된다.
2. 머신러닝의 장단점
   1. 예상치 못한 상관관계를 발견하는데 탁월하지만, 학습을 위해서 다양한 데이터가 필요하며, 결론 도출 과정을 일부 이해할 수 없는 블랙박스의 문제가 존재
3. 머신러닝 프로젝트 로드맵
   1. 문제를 정의하고 학습에 사용할 데이터를 살펴본 후 데이터를 일부 처리 후 분할한다. 선행 연구를 참고해 알고리즘을 선정하고, 데이터를 모델 input으로 적절하게 전처리 해주며 학습과 검증을 진행한다. 그렇게 최종적으로 학습된 모델을 테스트하고 문제가 없는 경우 시스템을 런칭한다.
4. 머신러닝의 종류
   1. 지도학습 : 정답(label)이 있는 학습 방법으로 비교적 학습이 쉽지만, 라벨링 작업에 비용이 든다는 단점이 있음
   2. 비지도학습 : 정답이 없는 학습 방법으로 입력 데이터만을 통해 학습. 라벨링 작업이 필요 없다는 장점이 있지만 성능 측정의 기준이 없다는 단점도 존재
   3. 준지도학습 : 일부 데이터만 정답이 존재하는 학습 방법으로, 레이블이 부족한 데이터셋에 유리하지만, 잘못된 데이터에 영향을 받을 확률이 높음
   4. 자기지도학습 : 정답을 임의로 만들어 학습하는 방법으로, 이를 통해 학습된 알고리즘은 다른 문제에 적용된다.
   5. 강화학습 : 특정 환경에서 상호작용하는 에이전트가 보상을 통해 학습하는 방법으로 특정 행동을 하도록 유도한다.
5. 선형대수
   1. 수의 집합을 연구하는 분야로, 스칼라, 벡터, 행렬, 텐서 등의 수의 집합을 공부
   2. 행렬을 덧셈과 뺄셈은 element-wise로 이루어지며 곱셈은 두 행렬의 행과 열의 내적으로 이루어짐
   3. Av = v’ 이를 선형 변환이라고 하며, 이 때 Av = λv인 경우 v를 A의 고유 벡터, λ를 A의 고유값이라고 한다. 고유 벡터는 A의 값이 가장 많이 분산되는 방향을 나타낸다.
6. 확률 분포
   1. 이산확률 분포의 경우, 동전 던지기와 같이 확률 변수가 이산적이며 셀 수 있는 경우를 의미하고, 모든 확률 변수의 확률 값의 합은 1이다.
   2. 연속 확률 분포의 경우, 특정 그룹의 키 분포와 같이 확률 변수가 연속적인 범위의 값을 취할 수 있는 경우를 의미하고, 모든 확률 변수 전 구간의 적분 값은 1이다.

궁금

• 선형 변환이랑 pca랑 뭔가 비슷한 구석이 있는 것 같다.
• 샘플링이 잘 이해가 안되네...! 다시 한 번 봐야겠다.