데브코스 47일차 - 머신러닝(선형회귀/분류)

키워드

사이킷런

패키지 소개

• 사이킷런: 다양한 머신러닝 알고리즘이 구현되어있는 오픈소스 패키지
  • 데이터 처리, 파이프라인, 학습 알고리즘, 전/후 처리 등 다양한 기능
• 객체 메소드
  • Estimator: fit()으로 학습 진행
  • Predictor: predict()로 예측 수행
  • Transformer: transform(), fit_transform()으로 데이터 변환
    • StandardScaler()가 이 중 하나임
  • Model: score()로 성능 평가
• 파이프라인: 머신러닝 워크플로우의 여러 단계를 하나의 수준으로 연결하는 작업
  • 가장 마지막을 제외하고는 모두 Transformer여야 함 (다음 과정으로 데이터를 넘겨주기 때문에
  • 마지막은 estimator, predictor, transformer가 올 수 있다. 이에 따라 파이프라인의 용도가 정해짐
• Numpy
  • 파이썬에서 과학적인 계산을 위한 패키지. 사이킷런에서 사용하는 기본 데이터 구조가 np.array임
• Pandas
  • 데이터 분석 기능을 제공하며, 데이터를 읽어들이는 데 사용됨
• Matplotlib
  • 데이터를 파탕으로 선 그래프, 히스토그램, 산점도 등의 다양한 시각화를 지원

지도학습의 개념과 대표 알고리즘

• 문제(Task): 머신러닝 기법을 활용해 해결하고자 하는 대상
• 지도학습에서의 문제
  • 회귀 문제 (Regression): 입력 데이터를 바탕으로 정확한 숫자 형태의 결과를 예측
  • 분류 문제 (Classification): 정해진 보기(class) 중 하나로 분류하는 문제
• 데이터 분할
  • 학습(정보 습득 및 이해) → 검증 (연습, 학습 상태 확인) → 시험(검증을 통해 최적의 공부 상태를 만들고 시험)
  • 학습 데이터: 순수하게 학습을 하는 데 사용하는 데이터 (전체 데이터의 약 80%)
  • 검증 데이터: 모델이 어느정도 학습되었는지를 학습 중 주기적으로 확인하는 데 사용 (약 10%)
  • 테스트 데이터: 모델의 최종 성능을 평가하기 위해 사용되는 데이터, 학습 과정에선 절대 사용되지 않음 (약 10%)
• 오버피팅
  • 모델이 특정 훈련 데이터에 지나치게 학습되어 새로운 데이터에서 잘 작동하지 않는 상태를 의미. 즉 일반화 능력이 떨어진 상태
  • 데이터 양을 늘리거나, 모델의 복잡도를 줄이거나, 규제(정규화 기법)를 사용해 문제 해결
• 손실함수
  • 모델의 예측값과 실제 정답 사이의 차이를 측정하는 지표
  • 모델의 학습은 손실을 줄이는 과정으로 진행됨
  • 손실함수의 종류는 문제의 유형(회귀, 분류)에 따라 다름
    • 회귀 → mse, 분류 → ce
• 파라미터
  • 모델이 내부적으로 갖고있는 변수를 의미. 데이터로부터 학습하는 패턴 관계를 표현, 모델의 예측 성능에 직접적인 영향을 미침
  • 최적화란, 모델의 성능을 최대화하거나 오류를 최소화하기 위해 파라미터를 조절하는 과정. 즉 loss가 최소가 되는 파라미터를 찾는 것을 목표로함
• 분류 문제 대표 알고리즘
  • 로지스틱 회귀: 이진 분류에 적합. 각 클래스의 확률을 예측
  • 결정 트리 분류기: 데이터를 잘 분할하는 결정 트리를 사용해 분류를 수행
  • 랜덤 포레스트: 여러 결정 트리의 결합으로 앙상블 기법에 해당. 과적합 문제를 방지
  • 서포트 벡터 머신: 데이터를 최적으로 분리하는 결정 경계를 찾는 데 강력한 알고리즘
• 회귀 문제 대표 알고리즘
  • 선형 회귀: 독립 변수와 종속 변수간의 선형 관계를 모델링
  • 라쏘 혹은 릿지 회귀: 규제 기법을 이용해 과적합을 방지하는 선형 모델
  • 결정 트리 회귀: 결정 트리를 회귀 문제에 적용
  • 서포트 벡터 회귀: SVM을 회귀에 적용한 알고리즘
  • K-최근접 이웃 회귀: 주어진 데이터 포인트에서 가장 가까운 k개의 이웃 데이터 평균으로 예측값을 결정. (데이터 의존도가 높음 → 비모수적 추정)

선형 회귀와 선형 분류

선형 관계

• 예를 들어 과자와 우유를 구매한다면, 전체 비용은 구매하는 과자와 우유의 개수에 영향을 받음
• 구매하는 과자의 개수, 우유의 개수는 서로 영향을 받지 않음 (독립 변수→ 상관성이 없어야 함)
• 이처럼 독립 변수(과자/우유의 개수)가 파라미터(가격) 값 만큼 일정한 비율로 결과 종속 변수(총 가격)에 영향을 미치는 관계를 선형 관계라 함.
• 파라미터들이 어떤 실수와 가중합(곱셈, 덧셈)으로 표현된 것을 선형 결합이라고 함
  • y = w1x1 + w2x2 + … + wnxn → 여기서 x는 독립변수이자 입력 데이터이며, w는 파라미터를 의미함. y는 종속 변수를 의미
• 만약 두 독립 변수 사이에 높은 상관관계가 있다면 다중공선성 이라는 문제를 일으킴

정규 방정식

• 선형 회귀 모델을 사용한다는 것은 입력 데이터 특징 사이의 독립성을 가정하고, 데이터 특징에 대한 선형 결합으로 회귀 문제를 풀겠다는 의미
• y햇 = w0 + w1x1 + w2x2 + … + wnxn = Xw → 독립 변수들이 선형으로 결합되어있음
  • w0은 y절편 (x랑 상관 없이 y에 직접적으로 영향을 미치는 변수) = 편향
  • X는 행렬(행은 하나의 데이터를 의미, 열은 특성을 의미), 0번째 열엔 모두 1이 들어감(w0을 위해)
• 비용 함수
  • 목표값과 예측값 사이의 계산을 통해 비용 함수를 정의. 즉 비용이 작아지면 정답과 예측값의 차이가 작아지는 것
  • 두 값 사이의 양적 차이(잔차)의 제곱 평균(MSE)로 비용함수를 정의
    • J(w) = (y-Xw)^2
    • 왜 절댓값을 사용할 수도 있는데 제곱을 사용하는걸까?
  • 즉 비용 함수를 최소화하는 파라미터들을 찾아야한다. min W ⇒ J(w)의 최소값 → 최소 제곱
• 최적화 방법론
  • 최적화: 특정 문제에서 최적의 해(보통 최소값 혹은 최대값)를 찾는 과정
  • 선형 회귀를 위한 최적화 방법은 정규 방정식(도함수가 0이 되는 지점을 계산)과 경사하강법이 존재
• 정규 방정식
  • 비용함수의 도함수 값이 0이 되는 파라미터가 최소값을 갖는 지점임
  • w = (X^TX)^(-1) X^T y
  • 이를 계산하는 시간 복잡도는 O(p^3)
    • p(특성 개수)의 3제곱에 비례. 즉 n(데이터 수)>>p(특성 개수)인 경우에 유용

확률적 경사 하강법

• 경사하강법 (Gradient Decent)
  • 비용함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 방법
  • 임의로 잡은 초기 파라미터 값을 기준으로, 비용 함수의 기울기를 계산해 기울기가 줄어드는 방향으로 파라미터를 수정
  • 비용 함수를 각 파라미터의 미분값(편미분)을 구해 기울기가 작아지는 방향(-기울기)로 learning rate만큼 이동
    • J(w) 편미분 → 2X(Xw-y)
    • W = W - 편미분값 * lr(학습률)
  • 모든 학습 데이터에 대해 기울기를 계산하므로 학습 데이터가 많은 경우 시간 소요 큼
    • 이를 해결하기 위해 전체 데이터 중 임의로 일부 데이터를 샘플링하여 그것을 대상으로 경사 하강법을 진행 → 확률적 경사 하강법 (Stochastic Gradient Decent)
    • 적은 데이터로 수정 이동을 반복하기 때문에 빠른 수렴이 가능
  • 적절한 학습률을 지정하는 것도 중요하다. 너무 크면 발산하고, 너무 작으면 학습이 잘 안된다.
  • 특성 수와 샘플의 수에 민감도가 적음

다중공선성

• 입력 데이터가 갖고있는 특징값들 사이에 상관관계가 존재할 때 발생하는 문제 상황

  • 이 상황에선 모델이 작은 데이터 변화에도 민감하게 반응 → 안정성과 해석력 저하

• 정규방정식으로 해를 구하는 상황에선 치명적인 문제가 발생

  • X^TX의 역행렬이 존재하지 않을 수 있음 → X^TX가 특이행렬인 경우

• 정규 방정식이 작은 데이터셋에선 매우 효과적이므로 SVD-OLS라는 방법을 사용하고자 함

  • 정규방정식으로 풀 수 없는 해를 다른 방식으로 구하는 방법 제시
  • 학습 데이터를 모아둔 행렬 X에 SVD를 적용해 특이값 분해(X = U sum V^T)
  • 이를 OLS 방식의 풀이에 적용해 해를 구하면, V sum^-1 U^T y
  • SVD-OLS는 O(np^2) ⇒ 대체로 n이 p보다 크기 때문에 SVD-OLS는 단순 OLS보다 오래걸림

• 만약 SVD-OLS를 사용했음에도 계산된 w값이 이상하다면(두 독립 변수 사이 상관 관계가 너무 크면),,, 선형이 아닌 다른 모델을 사용해야함

규제

• 과적합이 발생하면 w의 값이 매우 커지게 됨. 따라서 w 값이 너무 커지지 않도록 규제를 가해 과적합 문제를 회피하고자 하는 방법
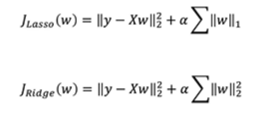
  • 줄여야하는 값인 비용함수에 w를 포함해 w도 줄이고자 함 → w 규제
    
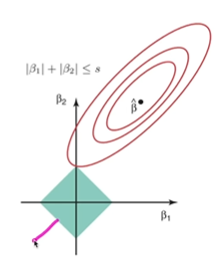
• 라쏘 회귀

  • w를 L1 norm(절대값을 모두 더함) 시킴

  • w가 꼭짓점으로 수렴되는 경향이 있음. 이는 일부 파라미터의 값을 0으로 만들 수 있음 → 불필요한 특성을 무시하는 효과를 가져올 수 있음

    

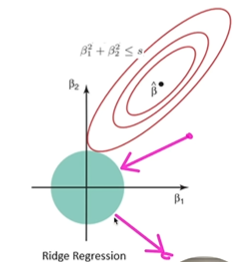
• 릿지 회귀

  • w를 L2 norm(제곱값을 모두 더해 루트를 씌움) 시킴

  • 파라미터 값을 적당히 작게 만듦

    

• 각각에 알파를 곱해 규제 강도를 조절함

선형분류

• 로지스틱 회귀

  • 이진 분류 문제에서 입력 데이터가 후보 클래스 중 각각의 클래스일 확률을 예측하는 모델
  • 즉 분류 문제를 회귀 방식으로 접근
  • 모델의 결과로 뽑아낸 logit을 로지스틱 함수(시그모이드)를 통해 로짓을 확률로 변경한다. 그리고 그 확률을 기준으로 0.5 이상이면 1, 아니면 0을 할당

• 다중 클래스 분류 문제

  • One vs One
    • A냐 B냐, B냐 C냐, A냐 C냐
  • One vs Rest
    • A가 맞냐 아니냐, B가 맞냐 아니냐, C가 맞냐 아니냐
  • Softmax Regression
    • 확률을 보고 클래스를 선택하는 것

• 오즈: 특정 사건이 발생할 확률과 발생하지 않을 확률의 비율 (p/1-p)

• 로그 오즈(로짓): 오즈에 로그 함수를 씌운 결과 (log(p/1-p))

  • 결과를 +- 무한대 범위를 갖도록 변환

• 로지스틱 함수: 로짓을 입력으로 주면 확률 반환 (0~1사이의 값) → 시그모이드

  • 시그모이드 = 1 / (1+exp(-x)) = p → logit을 x로 두고 p를 기준으로 정리

• 확률의 입장에서 변화량이 구간에 따라 다른 의미를 가짐 → 0.49 0.5 vs 0.98 0.99

• 비용함수

  • 로그 손실값을 사용
  • -(ylog(p햇) + (1-y)log(1-p햇))
  • 전체 학습 데이터에 대한 비용 함수는 모든 비용함수의 평균
  • 비용함수를 최소화 시켜야하는 최적화 문제. 즉 비용함수를 최소화하는 파라미터(w)를 찾아야함. 하지만 정규방정식과 같이 직접적으로 계산 가능한 해가 없기 때문에 경사하강법을 사용해야함

선형 회귀 모델 실습

• 보험료 데이터, 선형 회귀

EDA (탐색적 데이터 분석)

• 데이터 분석 초기 단계에서 진행됨. 데이터의 특징, 구조, 패턴, 이상치, 변수 간의 관계 이해
• 일반적으로 통계 분석(평균, 표준편차, 최소/최대값)
  • df.info(), df.describe()을 이용해 데이터 구성 요소 및 통계 분석 가능
• 시각화(패턴, 이상치, 경향성)
  • 분포 변환(log를 취해준다던지..), 이진 클래스로 변환 등
  • 카테고리형 변수 인코딩 (수치형으로 변경)
• 변수간 관계 파악(상관관계 분석)
  • corr() 사용
  • 두 변수간 너무 큰 상관관계를 갖는 경우 하나를 배제해야함 → 다중 공선성의 문제
• 이상치 탐지
  • boxplot으로 아웃라이어 확인
• 결측치 분석

전처리

• 원-핫 인코딩 (pd.get_dummies(data, drop_first=True)
  • 카테고리 데이터를 찾아서 원핫인코딩으로 변환, 즉 성별이라면 성별남성, 성별여성이라는 열을 새로 만들고 각각은 0 혹은 1로 표현. 근데 여기서 drop_first를 사용해 두 열 중 하나만 남김. 왜냐면 두 열을 모두 남기면 두 열 간 상관관계(?)가 선형 분류에 영향을 줘서 다중공선성이 나타날 수 있기 때문에
  • 그러면 지역 열을 get_dummies 할 때는 세개의 열이 남게되는데 그 사이의 상관관계는 문제가 되지 않는가?
• 특성 스케일링
  • 서로 다른 수치형 데이터 특성 사이의 값 범위를 비슷하게 맞춰주는 과정
  • 경사하강법을 사용하는 과정에서 수렴 속도를 높일 수 있음
  • StandardScaler(평균 0 표준편차 1로 조정, 데이터가 정규분포일때 사용), MinMaxScaler(최대값 1 최소값 0이 되도록 조정, 이상치가 큰 영향을 미치는 경우)
    ⇒ 데이터 특성에 따라 다양한 스케일링 방법을 적용할 수 있음

학습 후

• 예측 성능 확인

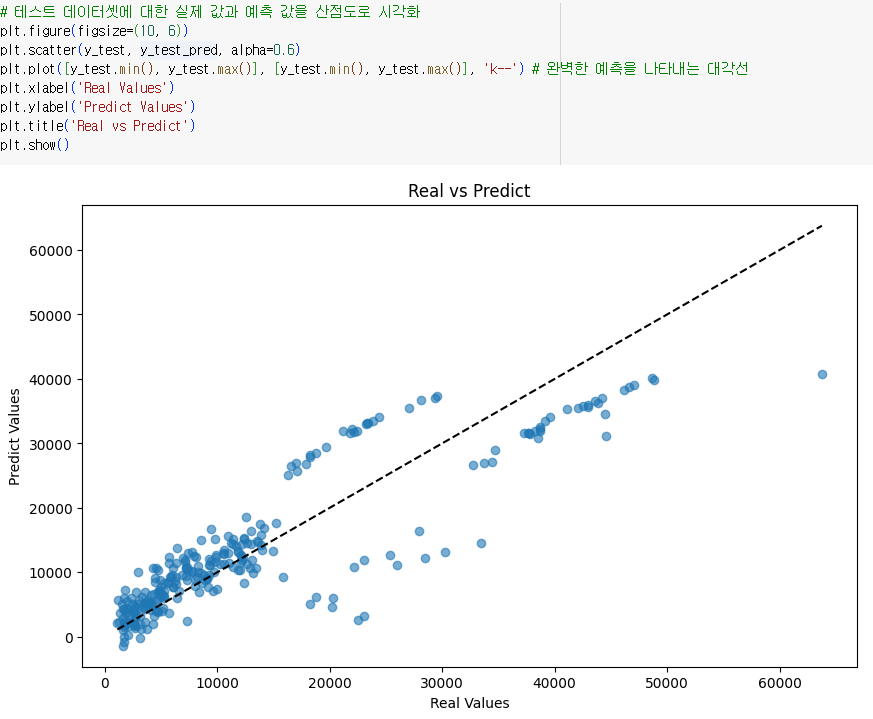
- 결과를 scatter로 그려보고 y=x 그래프(real values == predict values)를 그려서 모델의 예측 정확성을 확인해볼 수 있음
- 값이 커질수록 예측 정확도가 낮아짐

• 잔차 확인

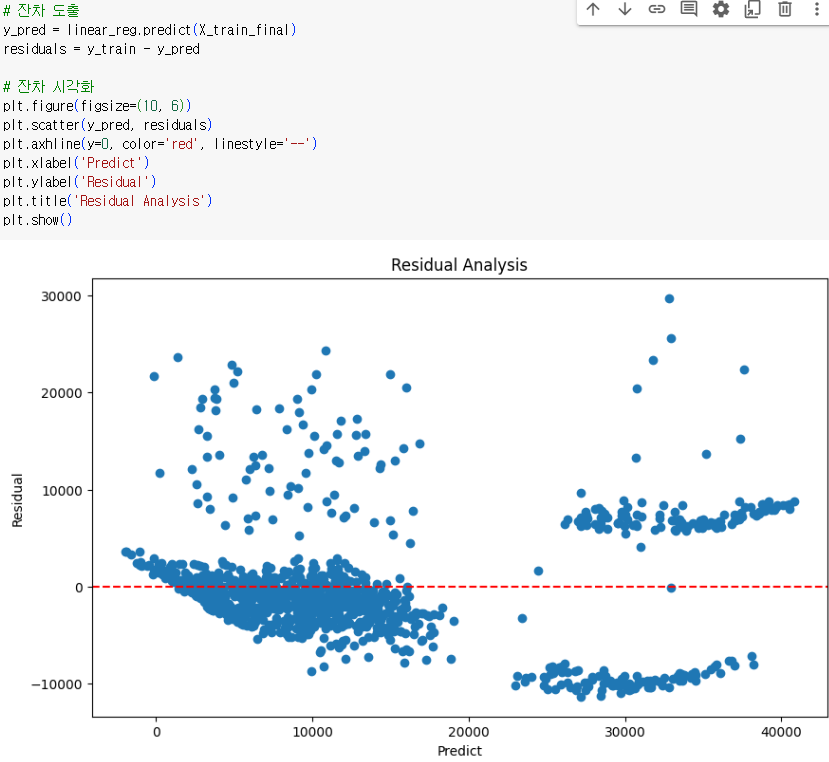
- 잔차(residual)을 확인해볼 수 있음. 무작위로 분포되어야 좋은 상황

• 변수 중요도

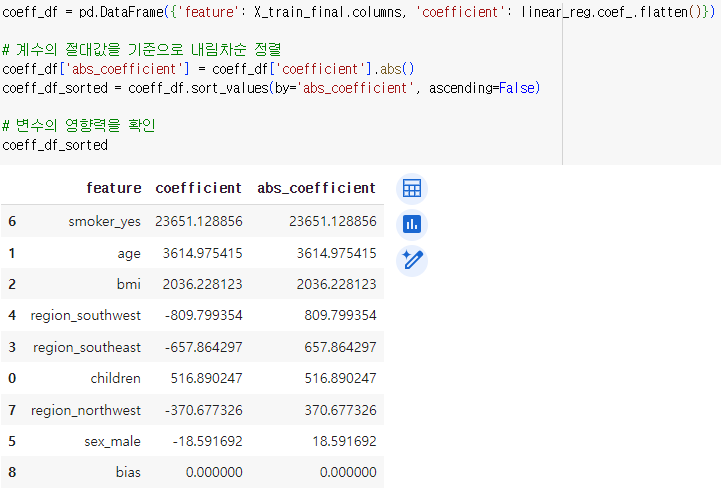
• .coef_ 를 사용해 y 예측에서의 각 피쳐의 중요도를 뽑아볼 수 있음

선형 분류 실습

• 비행 경험 만족도 데이터
• 탑승객의 개인 및 여행 경험 정보(독립변수)를 바탕으로 전반적인 비행 만족도(종속변수)를 예측

EDA

• 데이터 타입
  • 수치형
  • 서수형 : 순서나 등급을 나타냄. 순서는 중요하지만 그 차이는 균일하지 않음
    • ex) 0~5점의 만족도 점수가 있다면 0~1 차이와 2~3 차이가 동일하지 않을 수 있음
  • 범주형
• 시각화 (서수형 데이터)
  • 각 변수마다 보이는 분포가 상이함 → 상위점, 중간 점수에 몰림 현상
  • 서비스 개선의 입장에서 분포를 볼 수 있음
  • 만족과 불만족에 따라 분포를 확인할 수 있음
  • 상관관계를 확인해 대체해야할 변수를 찾아봐야함. 이 데이터엔 크게 없음

데이터 전처리

• 누락 데이터를 포함한 데이터 포인트는 제거 (dropna())
• EDA를 통해 판단한 제외 데이터 제거 → ex) 지연 시간 5시간 이상은 제거(거의 불만족을 줬을 것으로 예상되니..)
  • 이 과정에 정답은 없음
• 범주형 데이터에 대해 원핫 인코딩
• 데이터의 피쳐가 너무 많으니, 종속 변수와 상관관계가 큰 특성만 취하기
  • 결과 해석력/일반화 향상을 위해 상위 15개 변수를 취함

학습

• logistic regression 사용 → 15개의 특성(feature)를 사용하니 15개의 파라미터를 가짐
• 분류 모델은 정확도로 모델을 평가할 수 있음
  • confusion matrix를 사용할 수 있음
• coef를 이용해 각 특성의 중요도를 뽑아볼 수 있었음