1. DFS (Depth-First Search : 깊이 우선 탐색)
1) DFS란? (DFS를 따라가보자!)
"하나의 시작점이 어디까지 갈 수 있는지" 를 파악하기에 용이하다!
그래프의 DFS는 다음과 같은 특징을 갖는다.
- 임의의 정점으로부터 출발해, 그 자식의 자식의 자식까지 다 보고 → 다시 올라와서 → 다른 자식도 본다.
- 여러 자식 노드 중 선택할 때 나름의 규칙을 가지고 선택한다.
ex. 알파벳 순서 낮은 것부터
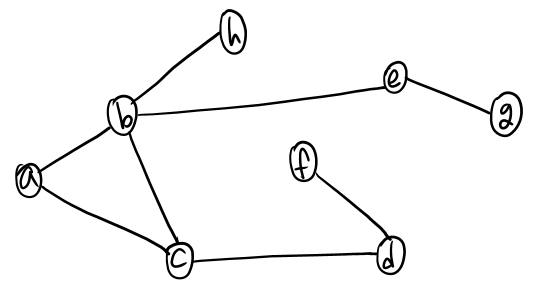
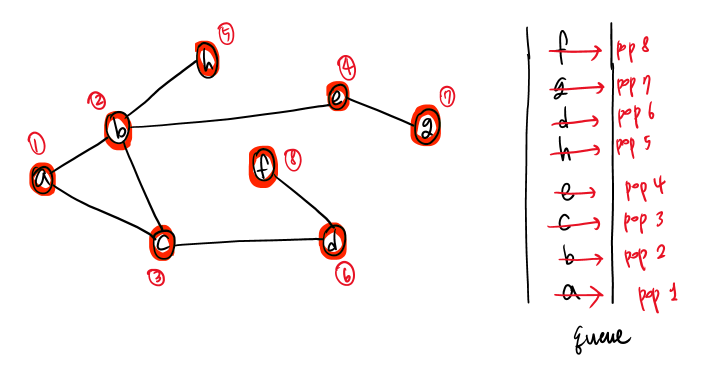
위 그래프를 가지고 DFS가 어떻게 동작하는지 따라가 보자!
(알고리즘을 이해하는 데에 있어, 글보다 그림이 더 효과적이라고 들었다..!)
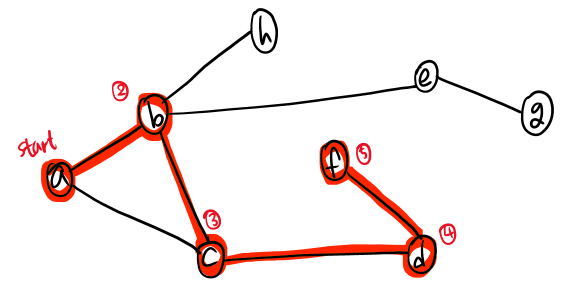
- 노드 a로부터 출발해서, b→c→d→f까지 따라 내려간다.
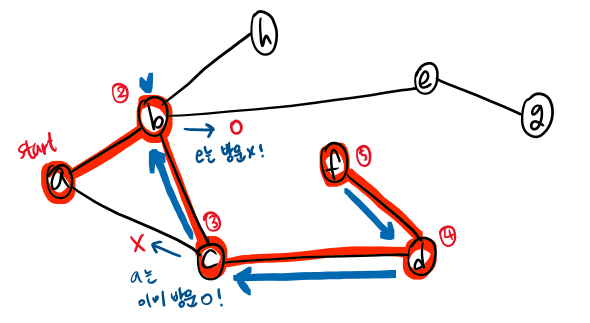
- f에서 더 이상 내려갈 자식 노드가 없으므로, 백트래킹을 반복하여 b까지 다시 돌아온다.
- b에 연결된 자식 노드들을 보니, 아직 방문하지 않은 노드가 있다!
e와 h 중 알파벳 순서가 더 낮은 e로 간다.
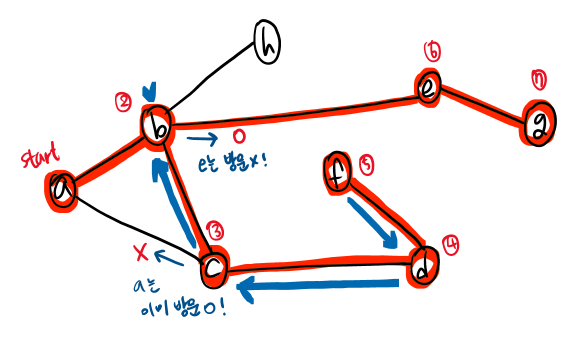
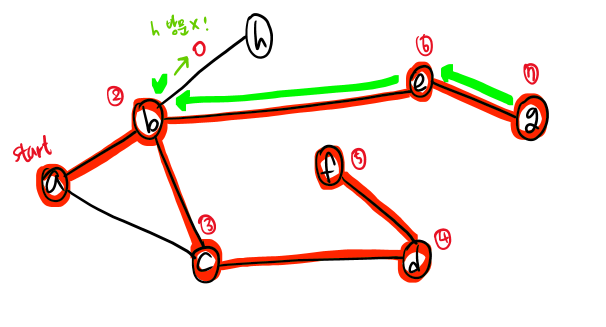
- e → g까지 방문한 후, g에서도 더 이상 방문할 자식 노드가 없으므로 되돌아가야 한다. (부모님의 부모님의 부모님 .. 근데 자식 노드가 남은..)
- 백트래킹 하여 b에 도착하면, 그 다음 자식 노드인 h로 간다. h는 아직 방문하지 않은 자식 노드이다.
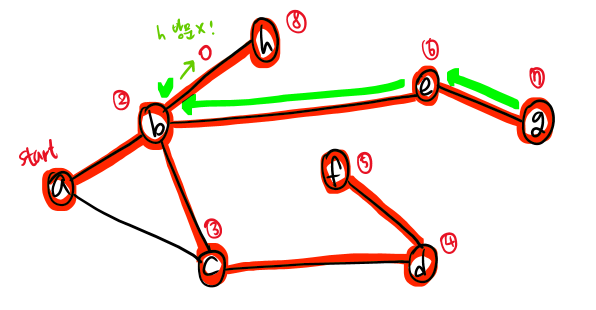
- h도 방문을 완료하면, 다시 백트래킹 하여 올라간다.
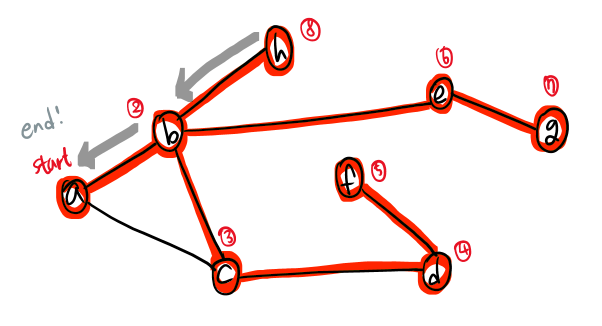
- 자식 노드가 남은 부모를 찾기 위해 백트래킹을 반복하다가, 결국에 시작 지점인 a 노드로 오게 되었고
- DFS는 끝난다!
2) DFS pseudo 코드
DFS 큰 틀은 다음과 같다.
DFS(now_node) is_visit = true for next node in connection_list if not visited DFS(next_node)이를 재귀/비재귀로 풀어보겠다!
1) 재귀 ver.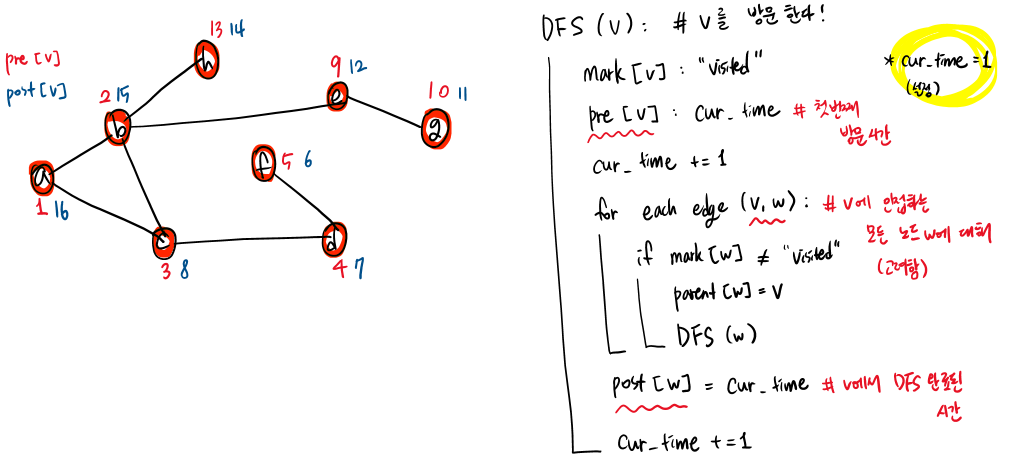
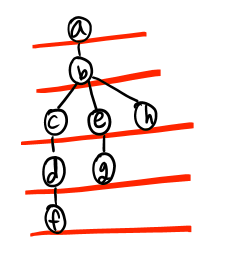DFS한 결과를 계층적으로 나타내 보면 위와 같다. DFS 한다는 것은 결국, 트리를 preorder traversal (전위 순회)한 것과 동일하다!
만약 연결된 edge가 없는 노드(isolated vertex)가 있는 경우라면, DFS가 가능할까?
가능하다!
DFS_ALL(G) 함수만 추가해 주면 된다.
그러면 짜잔..!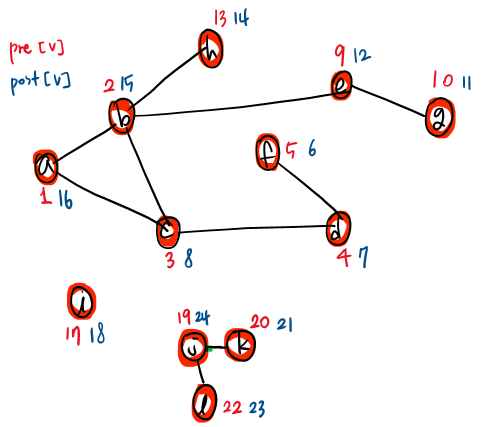 
2) 비재귀 ver. (Stack 사용)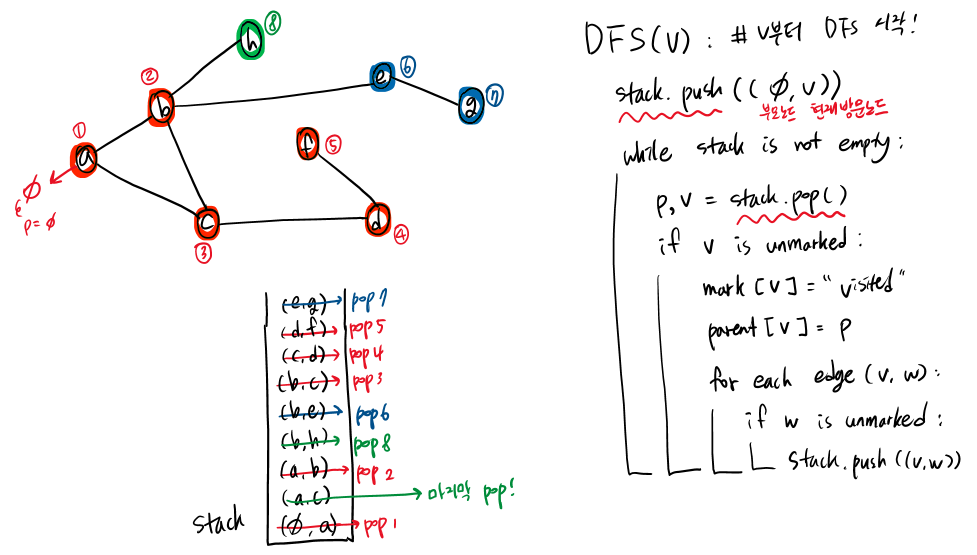 
- 처음 시작하는 노드는 부모 노드를 공집합으로 간주하고 스택에 넣는다. (edge를 넣는 것!)
- while 문이 시작되면
- 스택을 pop 하고
- pop된 edge에서 자식 노드가 아직 방문하지 않은 노드라면, 방문 처리를 하고
- 그 자식 노드와 인접한 모든 edge들 중 방문하지 않은 것만 스택에 push 한다.
※ 자식 노드 방문 규칙(ex. 알파벳 낮은 순서)을 고려하여, 방문 순서와 반대로 스택에 push 한다.
잠깐!
지금까지 살펴본 그래프는 undirected graph였다.
그렇다면, directed graph에서 DFS는 어떻게 작동할까? 이 개념이 바로 위상정렬이다. (위상정렬은 뒤에서 설명하겠다!)
2. BFS (Breadth-First Search : 너비 우선 탐색)
1) BFS란? (BFS를 따라가보자!)
"최단 길이를 보장한다"는 점에서 용이하다!
(레벨별로 인접한 노드들부터 탐색해 가기 때문에, 최단 경로를 알려준다.)
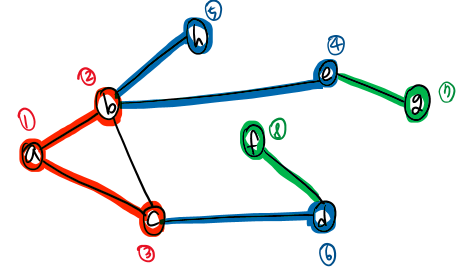
그래프의 노드 탐색 순서는 위와 같다.
- a 노드부터 출발해서 자식 노드인 b와 c를 먼저 탐색하고
- b의 자식과 c의 자식을 탐색하고
- b의 자식의 자식과 c의 자식의 자식을 탐색한다.
간단하다..! 그렇다면, BFS 알고리즘은 어떻게 접근해야 할까?
2) BFS pseudo code (Queue 사용)
BFS는 큐를 사용하면 뚝딱이다!
1. 큐에서 하나의 노드를 꺼낸다.
2. 해당 노드에 연결된 노드 중 방문하지 않은 노드를 방문하고, 차례대로 큐에 삽입한다.while queue not empty queue.pop() visit = True for next_node if not visited queue.push(next_node)
def bfs(start_vertex):
visited = [start_vertex]
queue = [start_vertex]
while queue: # queue를 모두 탐색할 때까지 반복한다.
v = queue.pop()
for adj_v in graph[v]: # 인접한 하위 노드를 모두 탐핵한다.
if adj_v not in visited: # 방문 처리되지 않은 노드에 대해서만 탐색한다.
visited.append(adj_v) # 해당 노드를 방문 처리 하고
queue.append(adj_v) # 해당 노드를 큐에 넣는다.
return visited BFS는 DFS와 달리 재귀로는 구현이 불가능하다.
DFS는 자식의 자식으로 내려가지만, BFS는 자식만 보고 다른 자식으로 넘어가야 하기 때문이다!
3. 위상정렬
핵심은 이거다.
부모 노드가 없는 것!
위상정렬은 directed graph일 때만 쓴다. 그리고 사이클도 없어야 한다.
(위상정렬의 시작점은 부모 노드가 없는 노드이기 때문에, 사이클이 존재하면 불가능하다!)
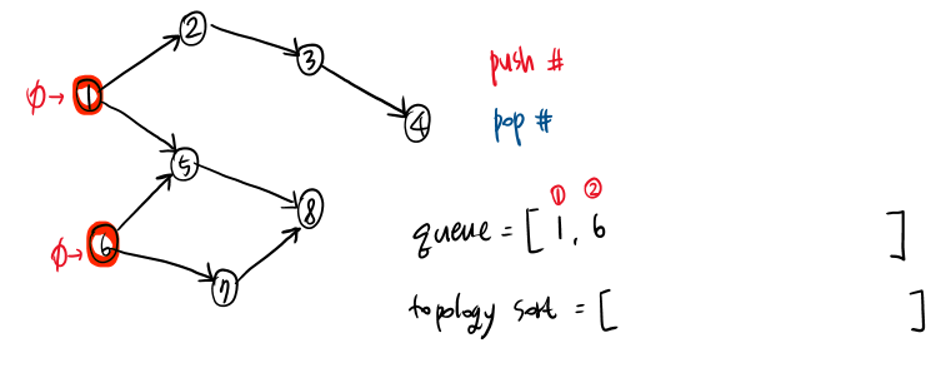
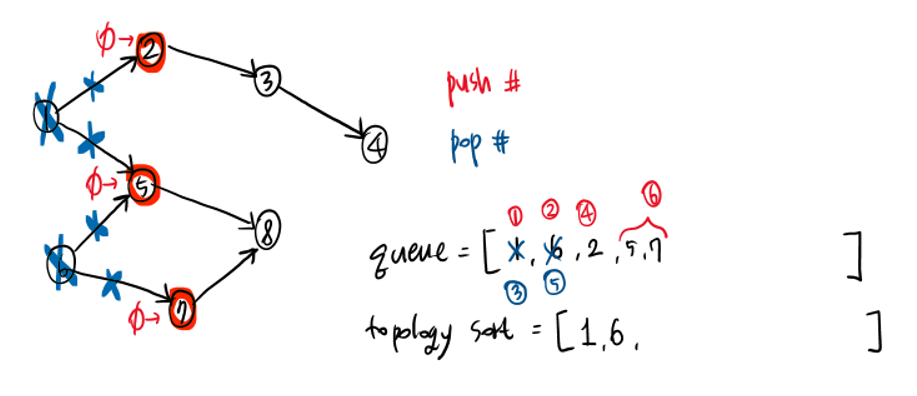
그림으로 따라가보면 다음과 같다.
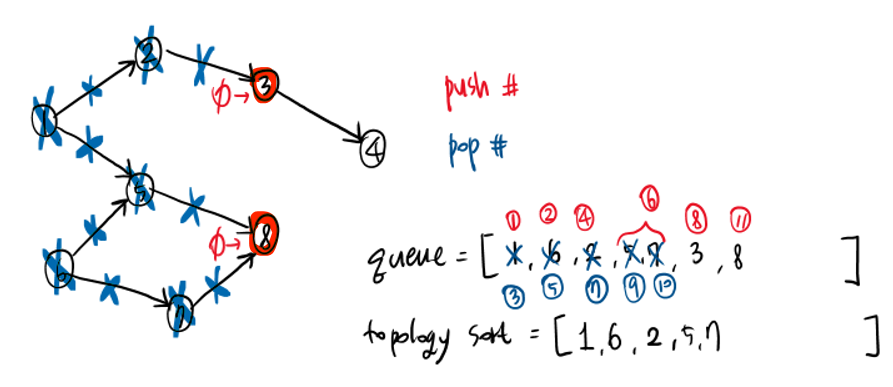
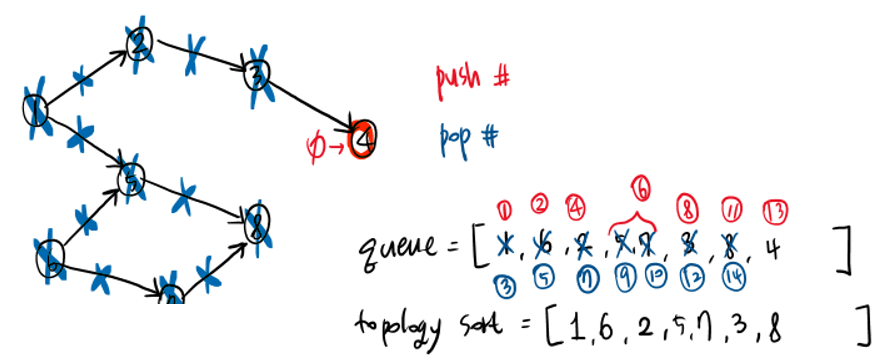이러한 과정을 거치면.. 결과는
위와 같다.
위상정렬 알고리즘
while queue: # 큐가 비어있지 않을 때까지 queue.pop() topological.push() for next_node parent -= 1 # 자식 노드에서 부모를 지우고 if !parent # 부모노드가 없다면 queue.append()
그 어떤 edge에 연결되지 않은 isolated vertex가 있어도 위상정렬이 가능하며, 이 경우에는 1 6과 함께 처음으로 큐에 들어갈 것이다. (topological sort에서도 1, 6, isolated_vertex 순으로 들어갈 것!)
