1. MST란?
MST(Minimum Spanning Tree)는 우리말로 풀어 쓰면 '최소신장트리'이다.
즉, 그래프가 주어졌을 때 모든 노드를 단 한 번씩만 거쳐 가되 (사이클 X), 이때 건너가는 모든 edge의 가중치 합이 최소가 되는 트리를 의미한다. MST를 구현할 때, 입력으로 주어지는 그래프는 undirected graph가 주이고, 출력은 최소신장트리(MST)이다.
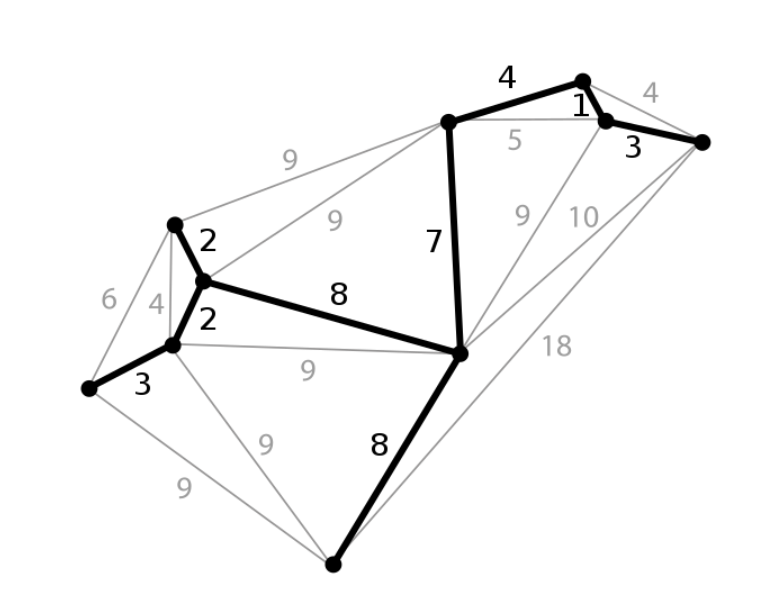(undirected graph→ 회색 선s / MST→검정 선s)
👆 잠깐! MST 대부분의 설명이 undirected graph를 가정하고 있길래, directed graph는 없는 건가..? 싶어서 찾아봤다.
directed graph에서도 MST와 비슷한 최소 신장 트리가 있는데, 이를 MDST라고 한다.
( 출처 : https://www.cs.tau.ac.il/~zwick/grad-algo-13/directed-mst.pdf )
MST를 본격적으로 뜯어 보기 전에..! MST가 왜 중요할까? (그냥 아무렇게나 선택하면 안돼?)에 대해 찾아봤다. 여러 면에서 MST가 유용하게 사용되지만, 특히 네트워크 망을 구축할 때 그 효용이 높다고 한다.
망 구축을 위해서는 모든 네트워크 포인트가 연결 되어야 한다. 네트워크 포인트는 양방향 연결로 이뤄지는데, 이때 회선의 수가 적을수록 비용은 효율적이다.
따라서, 각 노드를 모두 양방향(undirected)으로 연결하면서 최소한의 회선(edge)를 만들 수 있는 방법이 중요하다. 그리고 이에 사용되는 방법이 MST이다.
MST가 실생활에서 중요하게 사용된다는 걸 알게 되니, MST에 대한 애정이 샘솟는 것 같다..! 자, 이제 MST에 대해 본격적으로 탐구해 보겠다!
2. MST의 세 가지 성질
MST는 최소신장'트리'로, 트리의 성질을 고스란히 갖는다.
- n개의 node와 n-1개의 edge로 이뤄져 있다.
- edge를 삭제하면, 2개의 부트리로 분할 된다.
- 새로운 edge를 삽입하면, (해당 edge를 포함한) 사이클이 생성된다.
앞선 트리의 성질 이외에도 MST만의 특징 3가지가 더 있다.
1) Cycle C와 cutset D에 대해 |C∩D|는 짝수이다.
2) Cut Property
3) Cycle Property
1) Cycle C와 cutset D에 대해 |C∩D|는 짝수이다.
잠깐! cutset은 뭘까?
"정점 집합의 분할(S와 T) 가운데 S,T ≠ Ø인 것을 컷(cut)이라고 한다. 정점 한쪽 끝이 S, 그리고 다른쪽 끝이 T에 놓이는 간선들의 집합 D를 cutset이라고 부른다."
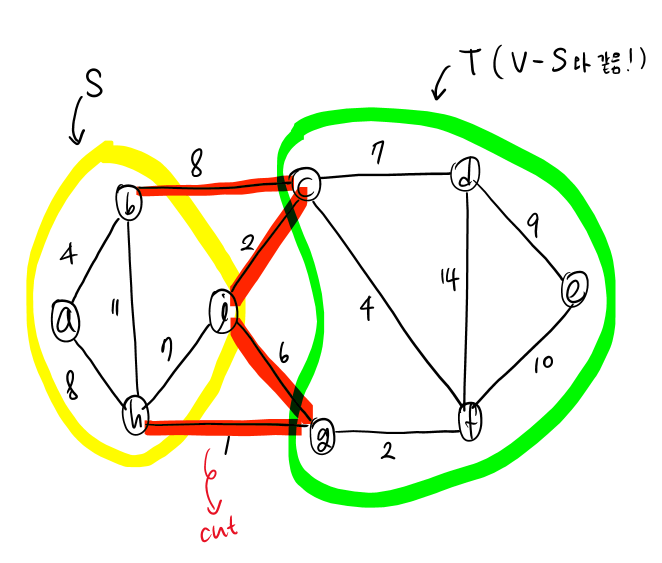
즉, 정점들의 집합을 S와 T(MST 포함/미포함)으로 분할 했을 때 양 집합 사이를 잇는 edge들을 cut이라고 하며, 이러한 edge들의 집합을 cutset이라고 한다.
그렇다면, MST의 첫 번째 성질인 "|C∩D|는 짝수이다."는 무슨 의미일까?
즉, 주어지는 그래프에서 시작 노드를 a로 설정했을 때, 다시 a로 돌아오기 위해서는 (사이클이 성립되기 위해서는) S와 T 사이의 이동은 짝수 번이 될 수밖에 없다는 것이다.
물론, MST는 '트리'이므로 사이클이 존재해서는 안 된다. 이 성질은 MST의 입력값으로 주어지는 그래프에서, "사이클을 찾는다면..?"에 대한 확인하는 명제일 뿐이다.
2) Cut Property
cut에서 최소(비용) edge를 포함하는 MST는 최소 하나 이상 존재한다.
MST의 2번째 성질인 Cut property는 MST에 꼭 들어가야 하는 edge의 성질을 표현한 것이다. 즉, (임의의) cutset D에서 가중치가 가장 작은 간선은 모든 MST에 반드시 포함된다는 의미이다.
이는 '귀류법'으로 증명할 수 있다.
만약 cut 중에서 최소 edge e와 (최소가 아닌) edge e'이 있다고 가정할 때,
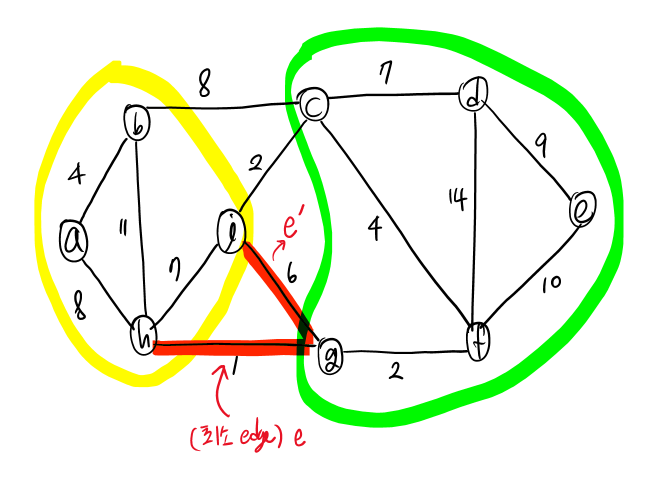
- T' = T - {e'} U {e}
※ 이때, T는 e'을 포함하는 MST라고 가정한다. - cost(e) < cost(e')
- cost(T') < cost(T)
이때 "최소"라는 모순이 생긴다.
따라서, cut 중에서 최소 edge는 반드시 MST에 포함될 수밖에 없다.
그리고 이러한 Cut Property를 이용한 알고리즘이 바로, Prim's Algorithm이다.
(뒤에서 설명하겠다.)
3) Cycle Property
임의의 cycle의 최대 비용 edge를 포함한 MST는 없다.
MST의 3번째 성질인 Cycle Property는 MST에 포함되지 않는(않아야 하는) edge의 성질을 표현하고 있다. 즉, 임의의 cycle에서 가중치가 가장 큰 간선은 어떠한 MST에도 포함되지 않는다는 의미이다.
이 또한 '귀류법'으로 증명할 수 있다.
cut 중에서 e가 최대 비용 edge일 때, (e'를 포함하는 MST를 T라고 가정하면)
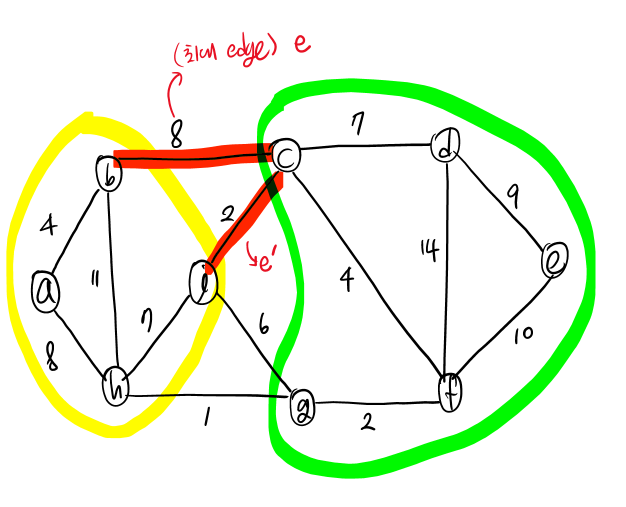
- cost(e') < cost(e)
- T' = T - {e} U {e'}
- cost(T') < cost(T)
이때, "최소"라는 모순이 생긴다.
따라서, cut 중에서 최대 edge는 그 어떤 MST에도 포함되지 못 한다.
그리고 이러한 Cycle Property를 이용한 알고리즘이 바로, Kruskal's Algorithm이다.
(곧 설명하겠다.)
3. MST 알고리즘 (1) - Prim's Algorithm
undirected graph에서 MST를 찾는 첫 번째 방법은 Prim's Algorithm(프림 알고리즘)이다.
1) 프림 알고리즘?
: 임의의 정점으로부터 출발해, 인접한 최소 비용 edge를 선택하면서 트리를 확장해 가는 알고리즘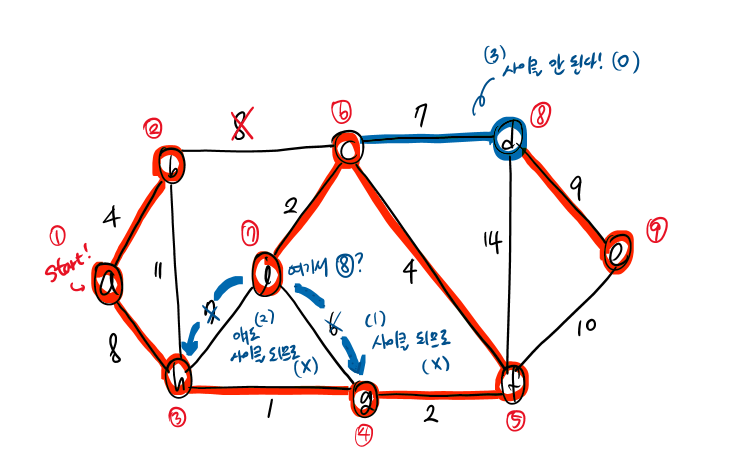 
시작 노드를 a로 잡고 출발했을 때,
- 9개의 node와 8개의 edge로 이뤄진 MST가 성립된다.
- 이때의 path는
(a b h g f c i d e)이다.
7번 노드에서 8번 노드로 넘어갈 때를 설명하겠다.
i 노드를 방문한 후, 그 다음 거쳐갈 edge의 후보는 (왼쪽에서부터)
(b,h)=11 / (b,c)=8 / (i,h)=7 / (i,g)=6 / (c,d)=7 / (f,d)=14 / (f,e)=10이 된다.
이때, 가중치가 가장 작은 (i,g)를 건너가려고 했으나, 사이클이 되므로 해당 edge를 버린다.
그러면 다음으로 가장 작은 (i,h)와 (c,d)가 7로 동일한데, 이때 어떤 걸 먼저 선택해도 상관 없다. 하지만, (i,h)를 선택하면 또 다시 사이클이 생긴다. 따라서 (i,h)도 버리고 (c,d)를 택한다. 이때 사이클이 형성되지 않으므로, 8번째에 거치는 노드는 d가 된다.
2) pseudo code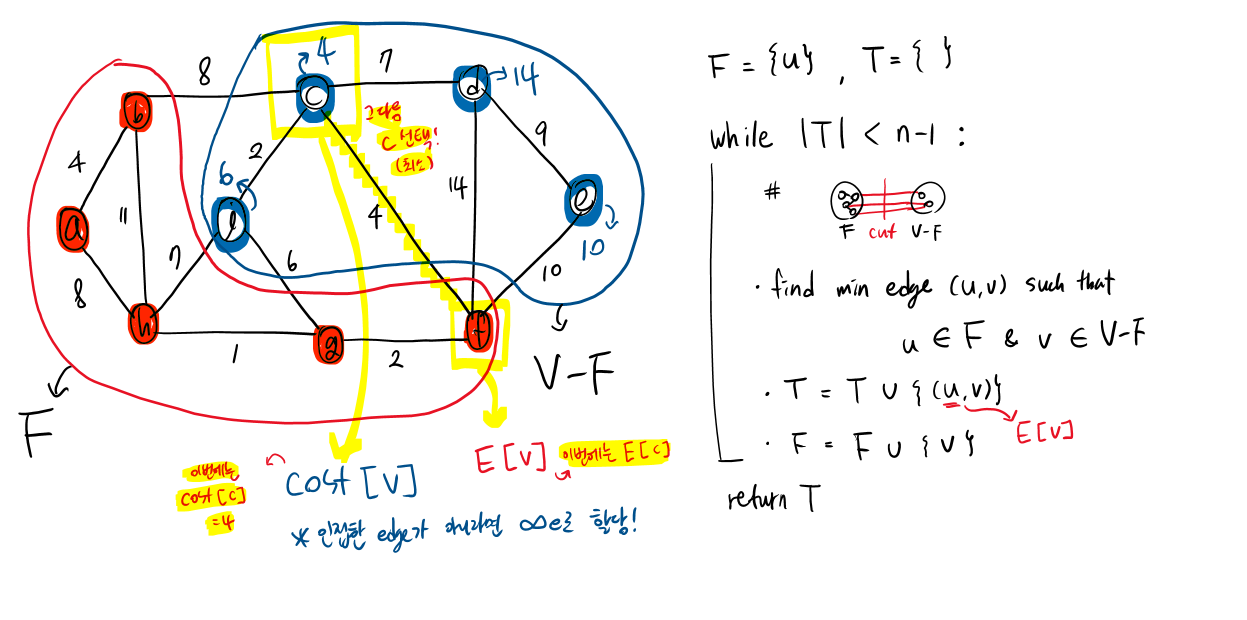 
F는 방문한 node들을,T는 거쳐간 edge들을 담는다.- (a b h g f)까지 MST가 형성 되었을 때, 그 다음 선택지는 V-F에서 선택한다.
이때 각 노드들은cost[v]값을 갖는데, 노드별 인접한 edge의 가중치 중 최솟값이다.
Prim's 알고리즘의 로직을 풀어 보면 다음과 같다.
- node를 방문 체크한다.
- node와 연결된 edge를 PriorityQueue에 append 한다. (PQ → Heap 사용)
- PriorityQueue의 맨 앞 원소를 pop 한다.
- pop 된 edge가 갈 수 있는 경우라면 → 연결한다.
pop 된 edge가 갈 수 없는 경우라면 → 다시 pop 한다. (3-4를 반복한다.)
이를 pseudo code로 작성하면 다음과 같다.
for each node v:
cost[v] = math.inf
E[v] = None
F[v] = False
T = []
Q = Heap(V, cost)
while Q is not empty:
v = Q.delete.min()
F[v] = True
if E[v] != None:
T.append( (E[v], v) )
for each edge (v, w) incident to v:
if F[w] == False and cost(v, w) < cost[w]:
cost[w] = cost(v,w)
Q.decrease_key(w, cost[w])
E[w] = v
return T- 그래프의 모든 정점에 대해 key값을 inf(무한대)로 할당한다.
- E[ ]는 각 노드들의 부모를 표시하는 리스트로, (임의의 노드 v의) 부모를 None으로 할당한다.
- F[ ]는 각 노드들이 방문 여부를 체크하는 리스트로, (임의의 노드 v의) 방문 여부를 False로 둔다.
- T[ ]는 거쳐간 edge들을 보관하는 리스트로, 시작은 빈 리스트이다.
- Q는 인접한 edge들을 담는 최소 우선순위 큐('힙')로, append 할 때마다 가장 작은 값이 맨 앞으로 정렬된다.
- Q가 비어있을 때까지 반복문을 수행하는데
- 매 반복문마다 cost값이 최소인 노드 v를 추출한다.
- v를 방문 체크하고, T에 (부모, 해당 노드) edge를 append 한다.
- 그리고 나서, 노드 v에 인접한 노드들에 대해
가중치와 노드의 key값을 비교해서 key 값이 더 크면 key값을 가중치 값으로 변경하고, 부모를 추출된 정점에 할당한다.
3) 시간 복잡도
Prim's 알고리즘의 시간복잡도는 '최소 우선순위 큐'를 어떤 자료구조로 구현하느냐에 따라 다르다. 대표적으로 Binary Heap과 Unsorted Array가 있는데, 각각 O(ElogV)와 O(|V|^2)이다.
일반화 된 시간복잡도 식은 다음과 같다고 한다.
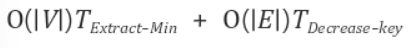(정점의 갯수 extract-min 수행시간) + (간선의 갯수 key값을 변경하는 데 걸리는 시간)
= 정점의 갯수만큼 최소 우선순위 큐에서 extract 하고, 인접한 간선의 갯수만큼 key값을 변경한다.
여기에서는 힙을 사용해서 구현하고 있으므로, O(ElogV)이 어떻게 계산되었는지 살펴보고자 한다.
- while 내부는 |V|번 수행되고, extract-min은 O(logV) 시간이 걸린다. → O(VlogV)
- for문은 O(E)번 수행되고, decrease-key는 O(logV) 시간이 걸리므로 → O(ElogV)
- O(VlogV + ElogV) = O(ElogV)
※ V + E를 E로 대체한다. (보통 노드보다 edge의 갯수가 더 많기 때문)
따라서, 힙으로 구현한 Prim's 알고리즘의 시간복잡도는 O(ElogV)이다.
4) 구현 코드 & 적용 예제
백준 1197번
import sys
import heapq
V, E = list(map(int, sys.stdin.readline().split()))
costs = [[] for _ in range(V+1)]
# 각 정점의 가중치와 인접 정보를 넣는다.
for _ in range(E):
node1, node2, weight = map(int, sys.stdin.readline().split())
costs[node1].append([weight, node2])
costs[node2].append([weight, node1])
# 방문 체크를 위한 리스를 만든다.
visited = [False] * (V + 1)
result = 0
cnt = 0 # len(edges) 대신 사용
# 최소 힙을 사용해서 우선순위 큐를 구현한다. (가중치 순으로 정렬되게 하여, 가장 낮은 cost를 고르도록 한다.)
edges = []
heapq.heappush(edges, (0, 1)) # (cost, start) 시작 지점은 1 노드, cost도 0
# 연결된 간선의 갯수가 V-1이 되면 종료한다.
while cnt < V :
# 우선순위 큐에서 가장 가중치가 낮은 걸 꺼낸다.
cost, start = heapq.heappop(edges)
if visited[start]: # 이미 방문한 노드라면 건너 뛴다.
continue
visited[start] = True
result += cost
cnt += 1
for c in costs[start]: # 방금 방문한 정점의 간선정보를 넣어준다.
heapq.heappush(edges, c)
print(weight)(추가) 다익스트라 알고리즘과 다른 점은..?
프림 알고리즘과 다익스트라 알고리즘 모두 그래프상의 모든 노드들을 (가능한 효율적으로) 연결한다는 공통점을 갖고 있다. 프림 알고리즘은 undirected graph에서만 가능한 반면, 다익스트라 알고리즘은 undirected/directed graph 모두 가능하다고 한다. 그래서 궁금증이 생겼다.
차이점이 이것밖에 없나..?
더 찾아보니까, 다음과 같은 차이점을 확인할 수 있었다.
“시작 노드가 지정되는지”의 여부와 "어느 것에 더 중점을 두는지" (최소비용 - 프림 / 최단거리 - 다익스트라)
프림 알고리즘의 경우, 시작 정점을 중요하게 생각하지는 않지만(어떤 정점으로부터 시작하든 상관 없지만) “반드시 최소 비용이어야 한다는 점”을 만족해야 한다.
반면, 다익스트라 알고리즘의 경우 “시작 정점으로부터 모든 노드가 각각 최단 거리로 연결 되어 있어야 한다는 점이 반드시 성립되어야 한다. 그리고, 어떤 정점을 시작으로 잡느냐에 따라 전체적인 비용이 달라질 수 있다고 한다.
따라서, 프림과 다익스트라 서로가 서로를 보장하지 않는다.
(즉, 최소 스패닝 트리가 최단 경로 트리를, 최단 경로 트리가 최소 스패닝 트리를 보장하지 않는다.)
4. MST 알고리즘 (2) - Kruskal's Algorithm
undirected graph에서 MST를 찾는 두 번째 방법은 Kruskal's Algorithm(크루스칼 알고리즘)이다.
1) 크루스칼 알고리즘?
: 가중치가 최소인 edge부터 연결해 가면서 트리를 확장해 가는 알고리즘
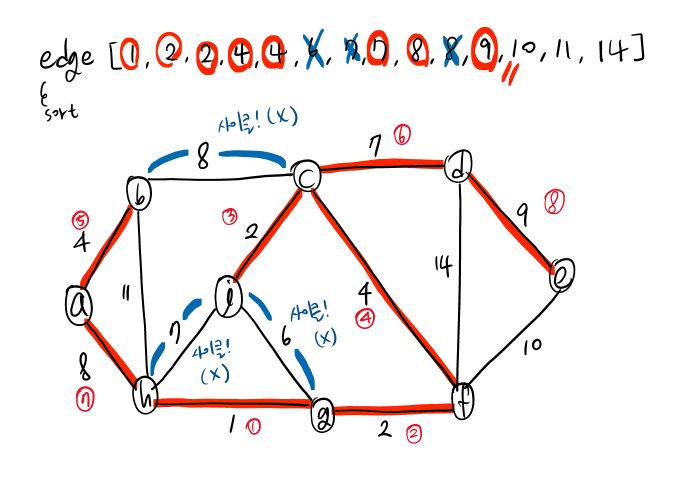Kruskal's 알고리즘은 시작 노드를 잡지 않는다. 대신, edge들의 가중치를 우선 정렬한 후 최솟값부터 선택해 나간다.
- 9개의 node와 8개의 edge로 이뤄진 MST가 성립된다.
- 다음에 선택한 edge로 사이클이 발생하면, 사이클 내의 최대 비용(가중치 최대) edge를 제거한다. → 방금 연결한 edge를 제거!
※ 안전 간선을 찾고 연결하는 위 과정에서,union find자료구조가 사용된다!
2) Union - Find
(인터넷에 올라온 정보들을 봐도 쉽게 이해 되지 않아, 정글 레드반의 '교수님'을 담당하고 있는 팀원에게 도움을 받았다. 역시 우리팀이 짱이다.👍)
Kruskal's 알고리즘은 노드를 기준으로 하는 게 아니라, 정렬된 edges들 중 가장 적은 비용(weight)부터 하나씩 연결해 가는 방법이다 보니, 이미 이어져 있는 노드 사이의 edge도 선택지로 들어가는 문제가 생긴다.
이러한 불필요한 edge들은 넣지 않기 위해, Union-Find 자료구조가 사용된다. (MST를 연결해 가는 과정에서 사이클이 발생하지 않도록 해 주는 셈이다!)
그림으로 좀 더 쉽게 설명해 보겠다.
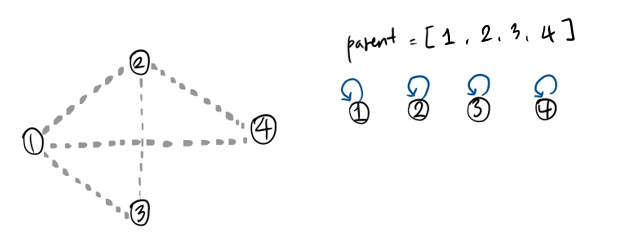
처음에, 그래프에서 edge들은 보이지 않고 node들만 있다고 가정해 보자.
각각의 노드는 자기 자신을 가리킨다. 즉, parent(부모)가 자기 자신이다.
※ 잠깐! 여기서 parent(부모)라고 한 부분은 집합의 대표값이라고 보면 된다! 즉, 연결된 노드들이 모인 집합을 대표하는 값으로, 부모 노드의 값이 될 수도 / 자식 노드의 값이 될 수도 있다고 한다. (어떤 값인지가 중요한 게 아니라, 동일한 값이라는 게 중요하다!)
대표값이 필요한 이유는 두 집합을 합칠 때(Union), 서로 같은 집합인지 아닌지 확인(Find)하는 데 필요하기 때문이다.
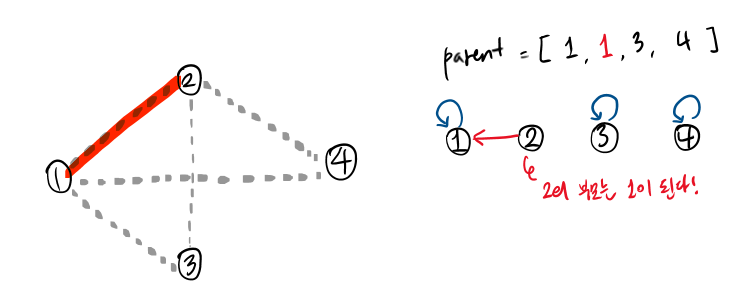그러다가 e(1,2)가 선택되었을 때, 2의 부모는 1이 된다. 이렇게 되면 1과 2는 부모가 같기 때문에 하나의 집합이 된다.
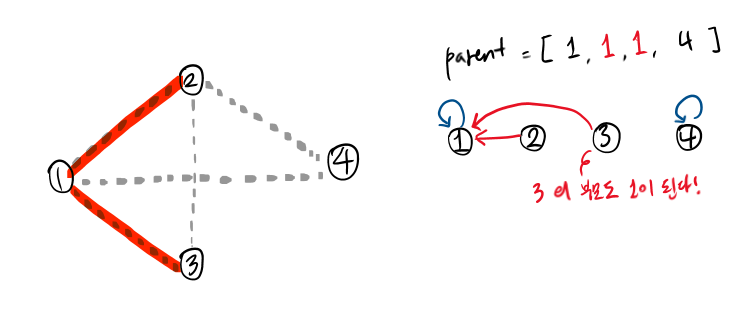이후 e(1,3)이 선택되면, 3도 마찬가지로 부모가 1이 된다. 이렇게 되면 부모가 같은 1, 2, 3은 동일한 집합에 있다고 본다.
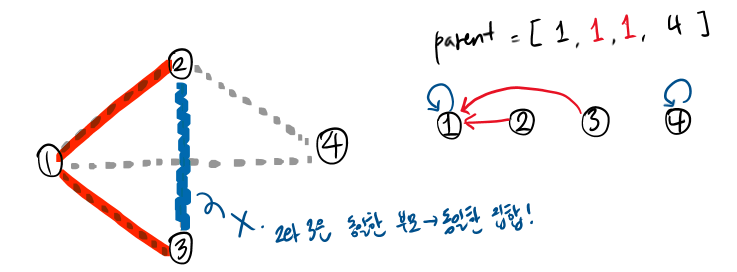만약, 그 다음 최소 비용 edge가 e(2,3)이라고 했을 때! MST에 들어가고 싶었던 e(2,3)이지만, 부모가 동일하므로 즉, 2와 3이 이미 같은 집합에 있으므로 e(2,3)은 버린다.
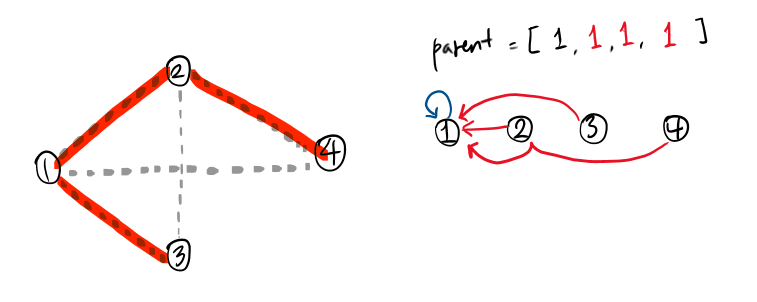마지막으로 남은 4는 부모가 다르므로, 4와 연결되는 edge 중 최소 비용 edge가 선택 되면 MST는 완성 된다!
3) ADT & 슈도 코드
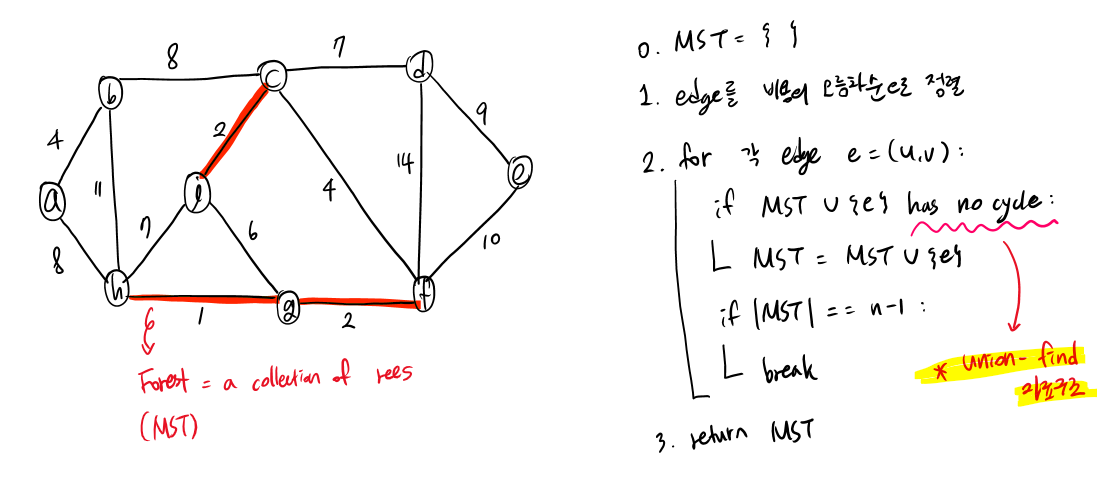
KRUSKAL(V, E):
T = [ ]
for each v ∈ E:
make_set(v)
sort E in non-decreasing order of weights
for each e=(u,v) in E:
if find(u) != find(v):
T.append(e)
union(find(u), find(v)) # union-find
return T0.
T는 Kruskal's 알고리즘의 결과가 되는 트리의 집합이다.
선택된 간선의 양 끝점이 다른 집합에 있다면 포함시킨다.
0+. 그래프의 모든 정점을 집합으로 만든다.make_set(v)
1. edge들의 가중치를 오름차순으로 정렬한다.
2. 각 단계를 진행할 때마다 최소의 가중치를 갖는 edge를 선택한다.
2-1) 이때, 모든 edge에 대해Union-Find연산을 수행한다.
2-2) Find 연산의 결과 두 집합이 다르면 edge를 MST에 추가시키고,
2-3) edge를 잇는 두 정점을 Union 한다.
3. n-1개의 edge로 이뤄진 T를 반환한다.
3) 구현 코드
백준 1197번
import sys
# 특정한 노드의 부모가 누구인지 찾는 함수 : find
def find(target):
if target == parent[target]:
return target
parent[target] = find(parent[target])
return parent[target]
# 부모 노드를 합치는 함수 : union
def union(a, b):
a = find(a)
b = find(b)
# 더 작은 값 쪽으로 부모 노드를 합침
if a < b:
parent[b] = a
else:
parent[a] = b
V, E = list(map(int, sys.stdin.readline().split()))
costs = []
visited = [1]
result = 0
for _ in range(E):
costs.append(list(map(int, sys.stdin.readline().split())))
# 크루스칼 알고리즘을 위해 가중치를 오름차순으로 정렬
costs.sort(key=lambda x: x[2]) # costs의 인자 중 세 번째 요소(weight)를 기준으로 정렬하겠다!
# parent → 부모노드가 누구인지 적혀있는 리스트
parent = [0]
for p in range(1, V+1):
parent.append(p)
for cost in costs:
start, end, weight = cost
# 두 노드가 사이클을 형성하지 않을 경우에만 합침
if find(start) != find(end):
result += weight
union(start, end)
print(result)4) 시간 복잡도
|V| = N, |E| = M이라고 가정하고 시작한다.
- 우선, |V|번의 make-set 연산(정점을 집합으로 만들기)를 수행한다. → O(N)
- 그 다음 edge들을 비내림차순으로 정렬한다. → M * O(logN)
- 이후, find와 union 연산을 수행하는데, 두 연산(함수) 모두 O(logN)만큼의 시간이 걸린다. 그리고 모든 edge에 대해 이를 반복하므로 → M * O(logN)
따라서, O(N + MlogN + MlogN)이 되고 결과적으로 O(MlogN)이 된다.
한 줄로 정리 하면,
O(E) 번의 Find와 Union 연산 + |V| 번의 make-set 연산 = O(ElogV)이다!
