[WEEK03] WIL 4-1. 그래프

1. 그래프란?

G = (V, E)

그래프(G)는 정점들의 집합(V, set of Vertices)과 간선들의 집합(E, set of Edges)으로 이뤄진 자료구조이다. 정점은 vertex, node로 간선은 edge, arc, link 등 여러 용어로 표현되기도 한다. 정점을 유의미한 데이터의 단위라고 한다면, 간선은 그 정점들간의 관계(정확히는 "관계가 있음")을 나타내는 도식 표현이다. 앞서 배운 트리 또한 그래프의 한 종류라고 볼 수 있는데, 단 트리는 '단방향성' 그래프이자 '사이클이 존재하지 않는' 그래프라고 할 수 있다.

핵심 키워드 #1. Edge

• edge : 간선

  • e = (노드1, 노드2)로 표현한다.
  • '노드1과 노드2는 인접하다(incident)'를 표현한다.
  • edge에 방향성이 있다면 → directed graph
    edge에 방향성이 없다면 → undirected graph

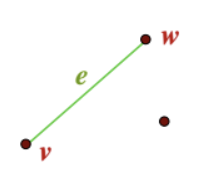
• isolated vertex : 연결된 edge가 없는 정점으로, 아래 그림 또한 그래프이다.

• parallel edges : 임의의 두 노드에 대해서 2개 이상의 edge가 있는 경우

• loop : 시작 노드와 끝 노드가 같은 edge
  
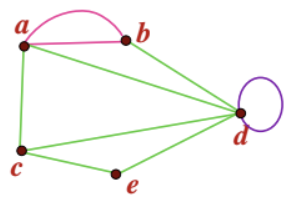
  위 그림에서 parallel edge와 loop를 찾을 수 있다.
  a and b are joined by two parallel edges 그리고 vertex d has a loop
  라고 표현할 수 있다.
  

핵심 키워드 #2. Path

• path : 경로

  • 노드n에서 노드m까지 도달하는데 거치는 모든 노드들의 순열(?)이다.
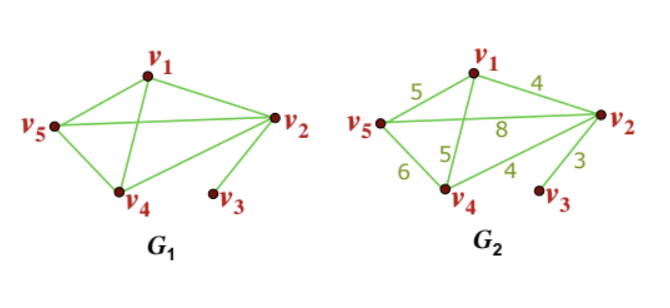
    ex. p = (v5 v2 v4 v1)
  • 모든 노드는 반드시 '한 번만' 거쳐야 한다. (두 번 이상은 path로 취급하지 않는다.)

• length of a path : 경로의 길이

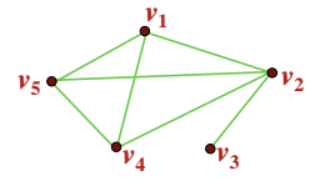
  • G1 : undirected graph
    • path에서의 edge 갯수이다.
    • path length of p : 3
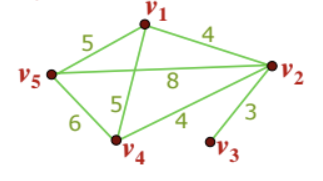
  • G2 : weighted graph
    • path상의 모든 edge의 가중치 합이다.
    • path length of p : 17

• degree : 분지수

  • '이웃한 노드의 갯수'를 의미한다. → 인접성
  • 각 노드별로도 degree를 가지고, 그래프 자체로도 degree를 가진다.
    (그래프의 degree는 모든 노드의 degree 중에서 최댓값이다.)

• cycle : 사이클

  • 처음(시작 노드)와 끝(마지막 노드)가 같은 path

3) Graph 종류

• Simple Graph : loop 혹은 parallel edges가 없는 단순한 그래프
  
• Weighted Graph : 각 edge별로 weight(가중치)가 있는 그래프 → 앞으로 주로 살펴볼 그래프다!
  
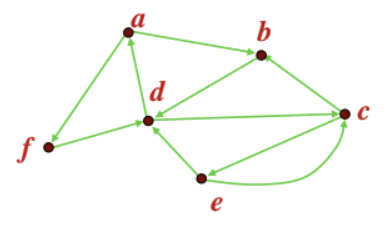
• Directed Graph (or Digraph) : 각 edge에 방향성(화살표)가 있는 그래프
  

앞서 살펴본 개념을 가지고, 아래 그래프를 파헤쳐 보자..!

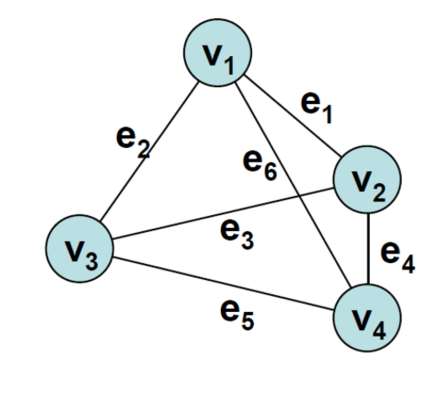
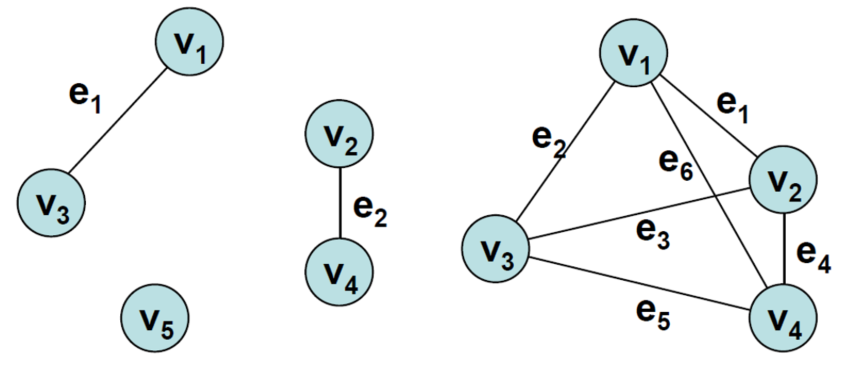
• 위 그림은 edge에 방향성이 없는 undirected graph (무방향성 그래프)이다.
  즉, e1 = (v1, v2) = (v2, v1) 모두 가능하다. (directed graph인 경우, 순서 중요함!)
• 위 그래프는 4개의 node와 6개의 edge로 구성되어 있다.
  V = {v1, v2, v3, v4}
E = {e1, e2, e3, e4, e5, e6}
• 집합 E의 각 edge들은 튜플로 표현할 수 있다.
  e1 = (v1, v2), e2 = (v1, v3), e3 = (v2, v3),
e4 = (v2, v4), e5 = (v3, v4), e6 = (v1, v4)
• 그래프의 degree는 3이다. (모든 노드가 각각 3개의 edge를 가지고 있다.)
• parallel edge나 loop는 없지만, cycle이 있는 그래프이다.

---

2. 그래프의 인접성

앞서, 그래프의 edge는 두 노드간에 "관계가 있음(incident)"을 나타낸다고 했다.
노드 간 edge의 유무 즉, 그래프의 인접성을 표현하는 방법에는 두 가지가 있는데 바로 인접 행렬과 인접 리스트이다.
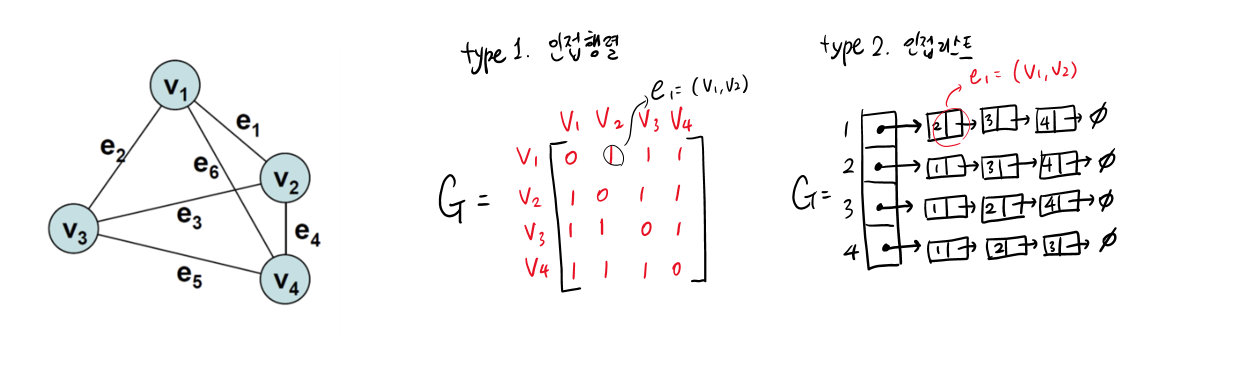(앞서 살펴본 그래프를 인접 행렬과 인접 리스트로 표현하면 위와 같다.)

그래프를 구현하기 위해 필요한 정보는 다음과 같다. (undirected graph)
1) 노드의 갯수
2) 간선의 갯수
3) 각 간선의 양 끝 노드

type 1. 인접 행렬 (adjacency matrix)

• 2차원 배열로 구현한다.
• 각 행과 열을 노드로 지정하고, 행과 열이 교차하는 지점은 0 또는 1로 표현한다.
• 두 노드 간에 edge가 있다면 1, 없다면 0을 넣는다.
• 만약 weighted graph인 경우, 1 대신 해당 edge의 weight를 넣는다.
• undirected graph인 경우 ↘ 방향으로 대칭을 이루지만, directed graph는 항상 대칭을 이루지는 않는다.

adjacency_matrix.py

import sys

node, edge = map(int, sys.stdin.readline().split())
adj = [[0 for _ in range(node) for _ in range(node)]]

for _ in range(edge):
    src, dest = map(int, sys.stdin.readline().split())
    adj[src][dest] = 1
    adj[dest][src] = 1

type 2. 인접 리스트 (adjacency list)

• 연결 리스트로 구현한다. (단방향, 양방향 모두 가능)
• 1차원 배열로 우선 그래프의 노드들을 다 집어 넣고, 각 노드에 연결된 edge들을 연결 리스트로 추가한다.
• 각 노드에 연결된 노드들은 순서대로 정렬할 필요가 없다.
• weighted graph인 경우, weight도 함께 표현할 수 있다.
  → 연결 리스트에 삽입하는 노드의 data를 (노드 번호, weight)로 한다.

구현.py

import sys

node, edge = map(int, sys.stdin.readline().split())
adj = [[] for _ in range(node)]

for _ in range(edge):
    src, dest = map(int, sys.stdin.readline().split())
    adj[src].append(dest)
    adj[dest].append(src)

---

3. 그래프 기본 연산

앞서 그래프를 인접 행렬과 인접 리스트로 표현해 보았다.
그래프의 인접성을 표현하는 방식이 왜 두 개나 될까? (물론, 두 개보다 더 많을 것이다..)

바로, 동일한 그래프이더라도 어떤 연산에는 인접 행렬이 또 어떤 때는 인접 리스트가 더 효과적이기 때문이다!

그럼, 그래프의 5가지 기본 연산을 가지고 인접 행렬과 인접 리스트를 비교해 보겠다!

G = (V, E) 에서 |V| = n, |E| = m이라고 할 때

1) 공간복잡도 (memory) : 인접리스트 승!👍

• 인접 행렬 : O(n^2)
• 인접 리스트 : O(n+m)

인접 행렬은 edge가 있는지 없는지에 상관 없이 무조건 n X n 개의 2차원 배열을 만들어 놓고 시작한다. 반면, 인접 리스트는 노드들로 1차원 배열을 만들고, 각 노드마다 edge가 있는 경우를 연결 리스트로 표현한다.(edge의 갯수 * 2 만큼만 더하면 된다.)
따라서, (그래프에 edge가 적은 경우) "메모리 낭비를 줄이고 싶다!" 하면 인접 리스트로 표현하는 걸 권장한다.

※ 추가로,
노드 갯수에 비해 edge가 상당히 적으면 → sparse / 상당히 많으면 → dense 하다고 한다.

2) (u, v) ∈ E ? : 인접 행렬 승! 👏

• 인접 행렬 : O(1)
• 인접 리스트 : O(n) → 최악의 경우

인접 행렬은 G[u][v] == 1 로 바로 찾을 수 있는 반면, 인접 리스트는 G[u].search(v) 로 u 노드에 인접한 노드들의 인접 리스트에 search() 함수를 써서 찾아야 한다. 만약 u에 연결된 노드가 n-1개라면(최악의 경우) n-1번의 연산을 수행하게 된다.

3) u에 인접한 모든 노드 v에 대해 (연산 수행) : 인접 리스트 승..? 👍

• 인접 행렬 : O(n)
• 인접 리스트 : O(인접 노드 수)

인접 리스트는 u에 연결된 head 노드부터 tail 노드까지만 따라가면 끝난다. (즉, 찾는 노드의 갯수는 u에 연결된 노드들만 보면 된다.) 반면 인접 행렬은 1부터 n까지의 모든 노드들을 확인해야 하기 때문에, (edge들의 상황에 따라 다르겠지만) 상대적으로 인접 리스트가 더 효과적이다!

4) 새로운 edge (u,v)를 삽입 : 무승부! 🏴

• 인접 행렬 : O(1)
• 인접 리스트 : O(1)

인접 행렬은 G[u][v] = 1 로 할당하면 되고, 인접 리스트는 G[u].pushFront(v) 를 하면 뚝딱 금방 끝난다! (연결 리스트로 표현할 때는 pushFront가 가능하지만, 리스트로 표현하면 append로 해야 한다.)

5) 기존 edge (u,v)를 삭제 : 인접 행렬 승! 👏

• 인접 행렬 : O(1)
• 인접 리스트 : O(n)

인접 행렬은 G[u][v] = 0 을 해서 기존 값 1을 0으로 바꾸기만 하면 된다. 반면 인접 리스트는 x = G[u].search(v) ▶ G[u].remove(x) 과정을 거치게 되므로 더 오랜 시간이 걸린다.

정리하자면,
5가지 연산에 대해, 경우에 따라서는 인접 행렬 혹은 인접 리스트가 더 우세할 수 있지만 메모리 측면에서는 인접 리스트가 짱이다!