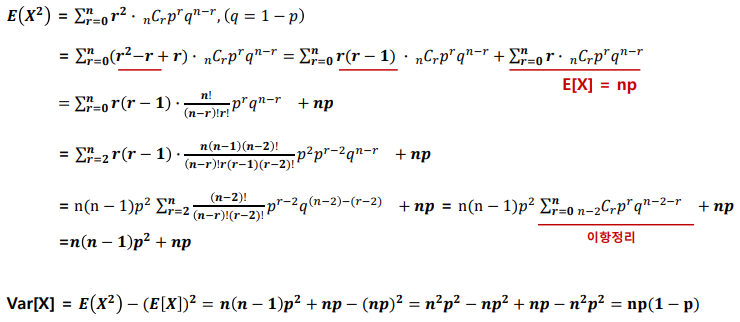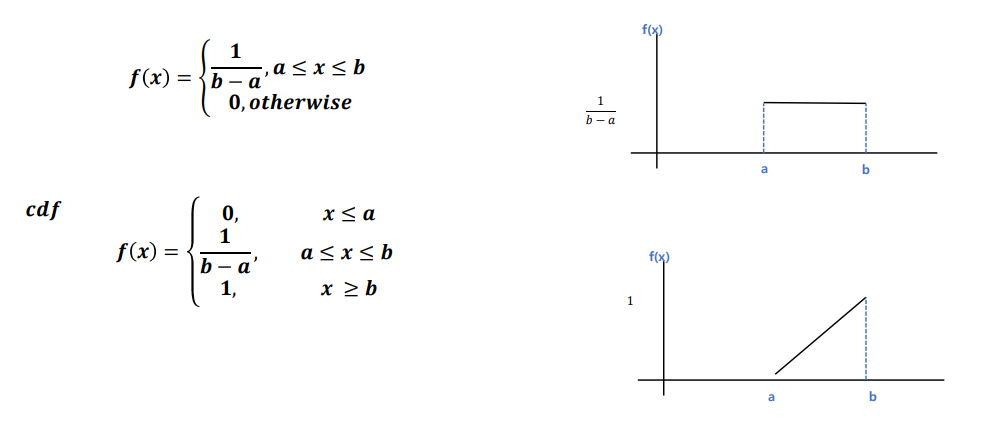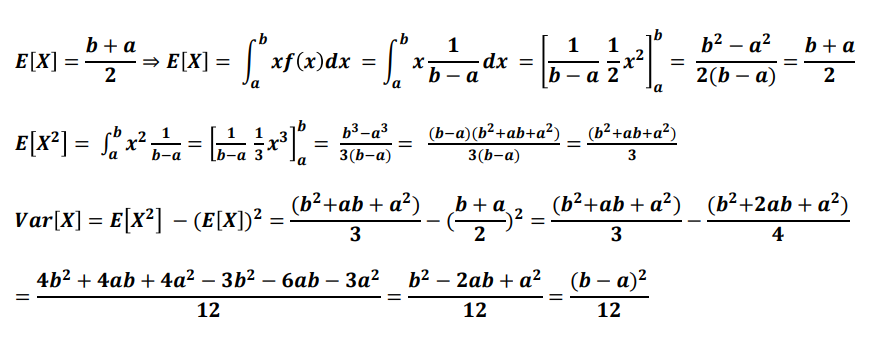해당 글은 제로베이스데이터스쿨 학습자료를 참고하여 작성되었습니다

1. 확률

• 모든 경우의 수에 대한 특정 사건이 발생하는 비율

표본공간

• 어떤 사건에서 발생할 수 있는 모든 결과의 집합

P(A) : 사건 A가 일어날 확률
S : 표본공간

$P(A) = \frac{사건\ A가\ 일어날\ 원소의\ 수}{표본공간\ S의\ 원소의\ 수}$

---

팩토리얼(N!)

• n개를 일렬로 늘여놓은 경우의 수

$n!\ =\ n\left(n-1\right)\left(n-2\right)...\cdot 2\cdot 1$

---

순열(Permuation)

• 순서를 고려하여 n개 중 r 개를 뽑아서 배열하는 경우의 수

$_nP_r=\frac{n!}{\left(n-r\right)!}=n\left(n-1\right)\left(n-2\right)\times ....\times \left(n-r+1\right)$

---

조합(Combination)

• 순서를 고려하지 않고 n개 중 r개를 뽑아서 배열하는 경우의 수

$_nC_r=\frac{_nP_r}{r!}=\frac{n!}{r!\left(n-r\right)!}$

---

조건부확률(conditional probability)

• 어떤 사건 A이 발생했을 때, 또 하나의 사건 B가 발생할 확률

$P\left(B\mid A\right)=\frac{P\left(A\cap B\right)}{P\left(A\right)},\ P\left(A\right)\ne 0$

$P\left(A\cap B\right)=P\left(B\mid A\right)\cdot P\left(A\right)=P\left(A\mid B\right)\cdot P\left(B\right)$

---

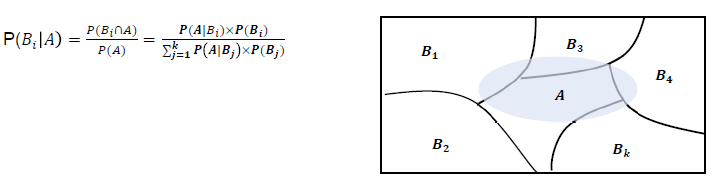
베이즈정리(Bayes's Theorem)

• 표본 공간 S에서 서로 배반인 사건 B1,B2, ..., Bk에 의하여 분할 되어 있을 때, 임의의 사건 A에 대하여 다음이 성립함
  

---

2. 확률변수

• 표본 공간에서 각 사건이 발생할 확률을 표현한 변수

확률 변수의 평균 : 기대값

$E\left(X\right)=\sum _{i=1}^n{x}_iP\left({x}_i\right)={x}_1P\left({x}_1\right)+{x}_2P\left({x}_2\right)+...+{x}_nP\left({x}_n\right)$

---

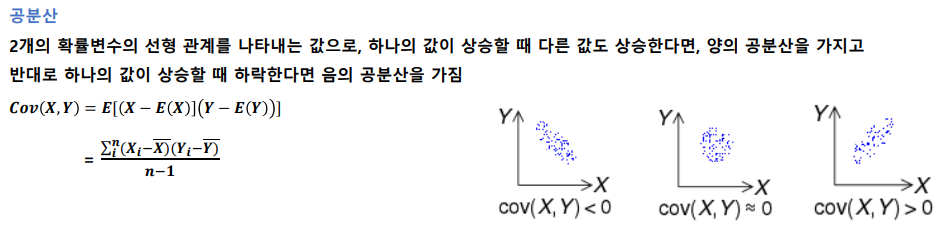
확률 변수의 분산

$Var\left(X\right)=\frac{1}{N}\sum _{i=1}^n\left(x_i-\mu \right)^2$

---

3. 이산형 확률분포

확률분포

• 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수
  

---

이산형 균등분포

• 확률 변수 X가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포
  

---

베르누이

• 베르누이 시행 : 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행
• 베르누이 분포 : 베르누이 시행인 확률 변수의 분포
  

---

이항분포

• 서로 독립인 연속적인 베르누이 시행
  

---

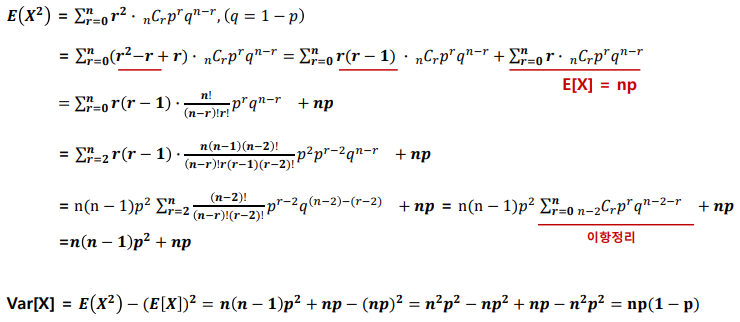
포아송 분포

• 어느 희귀한 사건이 어떤 일정한 시간대에 특정 횟수만큼 발생할 확률분포
  

---

이항분포의 포아송 근사

• B(n,p)를 조건(n>30, p<<1, $\lambda = np < 5$)을 충족하면 포아송분포로 근사 가능
  

---

기하분포

• 어떤 실험에서 처음 성공이 발생하기 까지 시도한 횟수 X의 분포(베르누이 시행)
  

---

음이항분포

• 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률분포
  

---

이산형 확률 분포 요약

---

4. 연속형 확률분포

확률밀도함수(PDF)

• 연속형 확률 변수 X에 대하여 함수 $f(x)$가 아래의 조건을 만족하는 경우
  

---

누적분포함수(CDF)

• 확률밀도함수를 적분한 함수
  

---

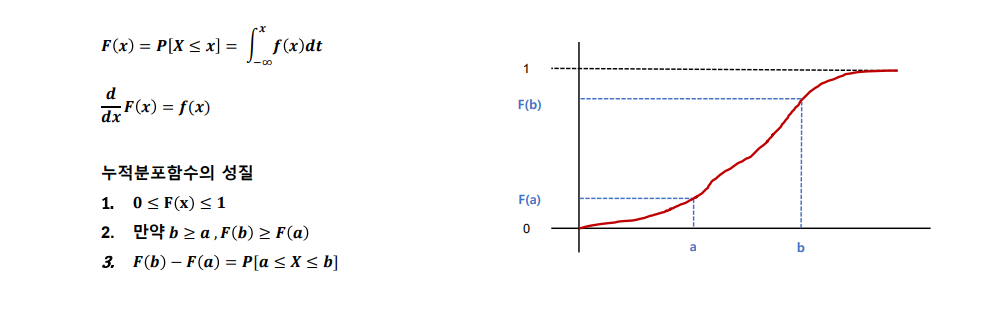
균일분포

• 확률변수 X가 a와 b사이에서 아래와 같은 확률밀도함수를 갖음
  
  

---

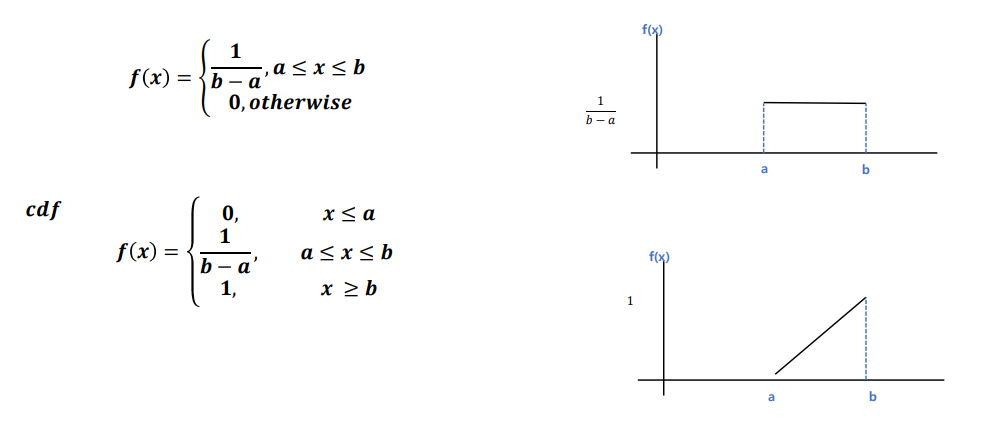
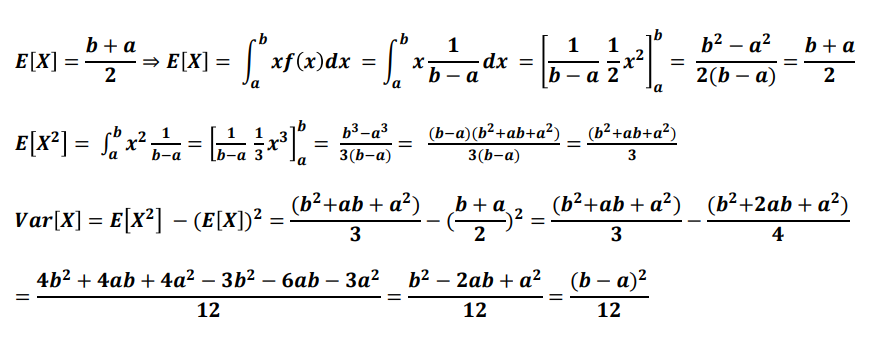
정규분포(가우스분포)

• 확률변수 X가 평균이 $\mu$이고, 분산이 $\sigma^2$인 정규분포
  
  

---

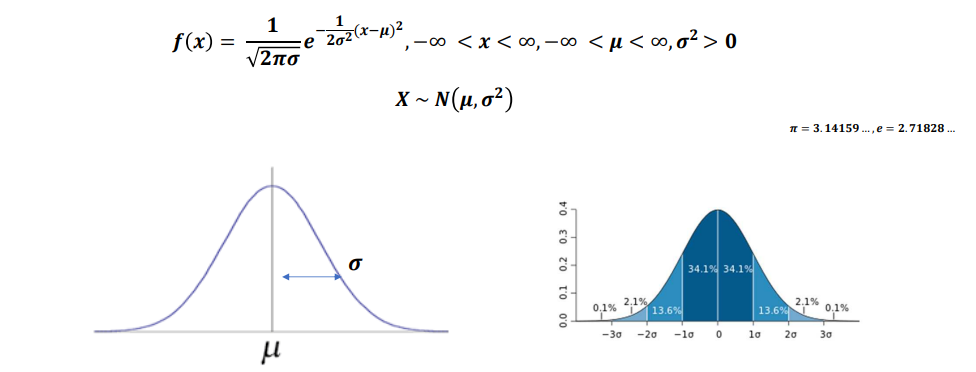
표준정규분포

• 확률변수 $X$~$N({\mu},{\sigma^2})$인 정규분포를 따르고, 확률변수 $Z = \frac{X-\mu}{\sigma}$라고 할 때 확률변수 $Z$~$N(0,1)$라고 한다
  

---

이항분포의 정규근사

• $X$~$B(n,p)$일 때, 확률 변수 X는 n>30이면 근사적으로 정규 분포 $X$~$N(np, npq)$를 따름
  

---

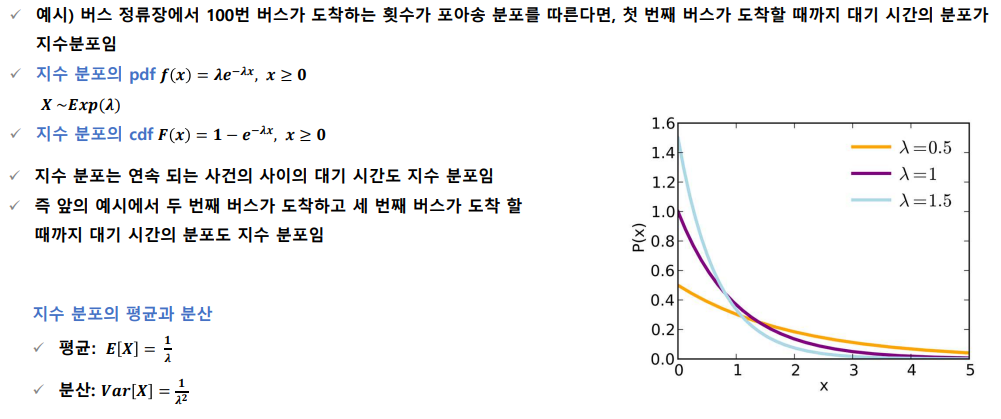
지수분포

• 단위 시간당 발생할 확률 $\lambda$인 어떤 사건의 횟수가 포아송 분포를 따르다면, 어떤 사건이 처음 발생할 때까지 걸린 시간 확률 변수 X는 지수 분포임
  
  
  
  

---

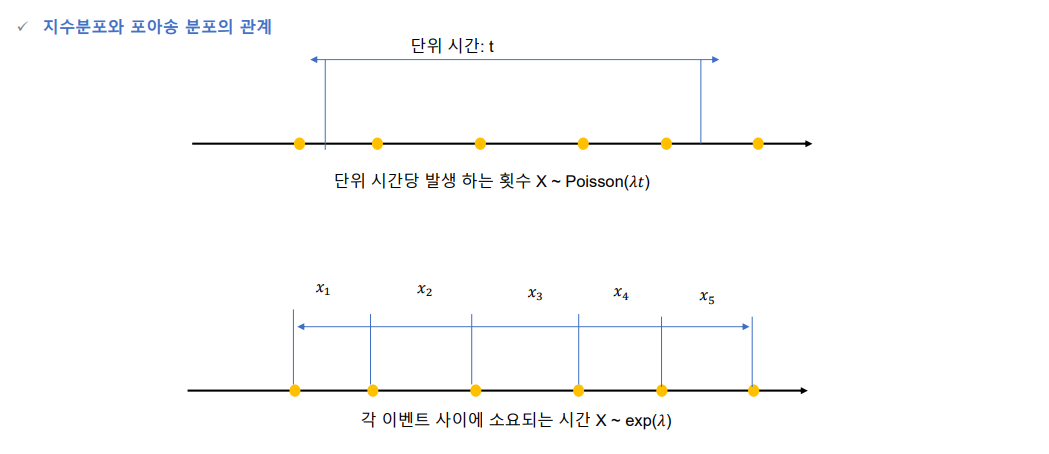
확률분포의 관계도