해당 글은 제로베이스데이터스쿨 학습자료를 참고하여 작성되었습니다
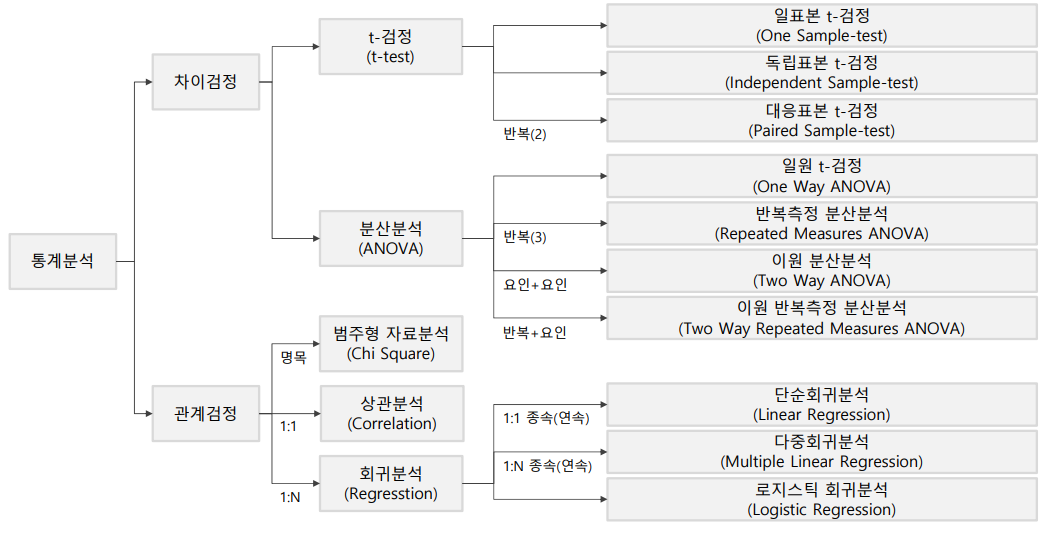
1. 범주형자료분석
- 범주형 자료
- 관측된 결과를 어떤 속성에 따라 몇 개의 범주로 분류시켜 도수로 주어진 데이터
- 범주형 자료 분석
- 범주형 자료에 대한 통계적 추론 방법
- 범주형 자료 분석은 카이제곱 검정으로 추론함
1-1. 적합도 검정
- 관측된 값들이 추론하는 분포를 따르고 있는지 검정, 한 개의 요인을 대상으로 검정

1-2. 독립성 검정
- 관측된 값을 두 개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지 독립성을 검정

1-3. 동질성 검정
- 서로 다른 세 개 이상의 모집단으로 관측된 값들이 범주내에서 동일한 비율을 나타내는지 검정

2. 상관&회귀 분석
2-1. 상관분석
- 두 변수 간의 함수 관계가 선형적인 관계가 있는지 파악할 수 있는 측도


2-2. 회귀분석
- 회귀분석
- 변수들간의 함수적 관계를 선형으로 추론하는 통계적 분석 방법으로 독립변수를 통해 종속변수를 예측하는 방법
- 종속 변수
- 다른 변수의 영향을 받는 변수, 반응변수, 예측 하고자 하는 변수
- 독립 변수
- 종속변수에 영향을 주는 변수, 설명변수, 예측 하는 값을 설명하는 변수
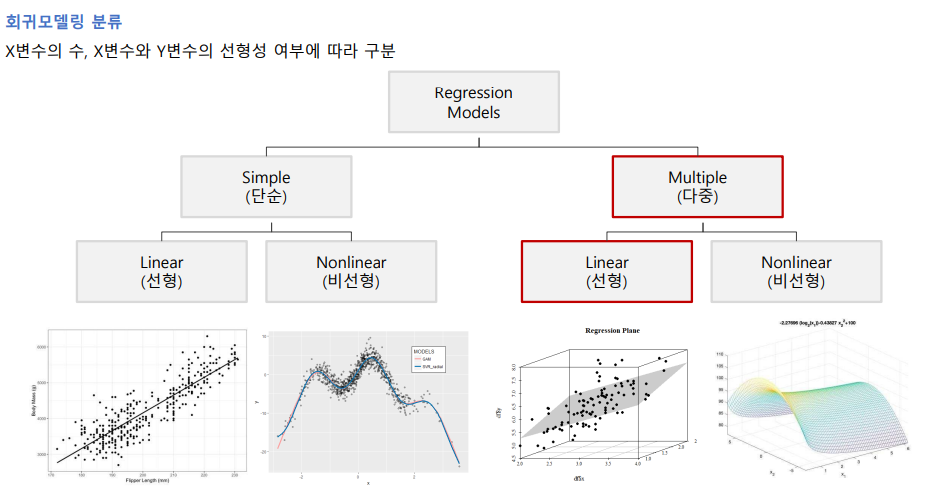
회귀분석의 종류
- 단순 회귀분석
- 하나의 독립변수로 종속변수를 예측하는 모형
- 다중 회귀분석
- 2개 이상의 독립변수로 종속변수를 예측하는 회귀모형
1) 단순회귀분석
- 하나의 독립변수로 종속변수를 예측하는 모형
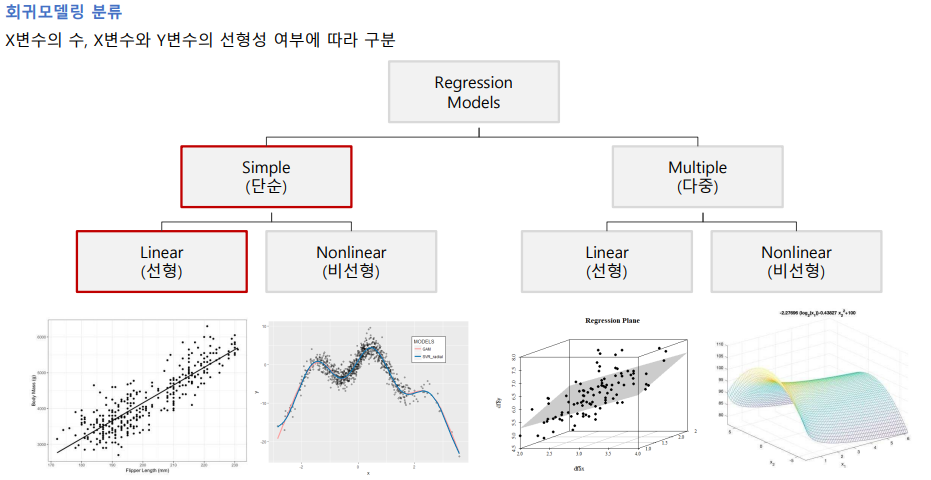

최소제곱법(최소자승법)(Least Mean Square)
- 회귀 모형의 모수 , 을 추정하는 방법중 하나를 최소 제곱법이라고 하며, 회귀 모형의 모수를 회귀 계수
- OLS(Ordinary Least Square) : 최소제곱법을 통한 회귀모형의 모수 추정
- LSE(Least Square Estimation) : 최소제곱법을 통해 구한 추정량
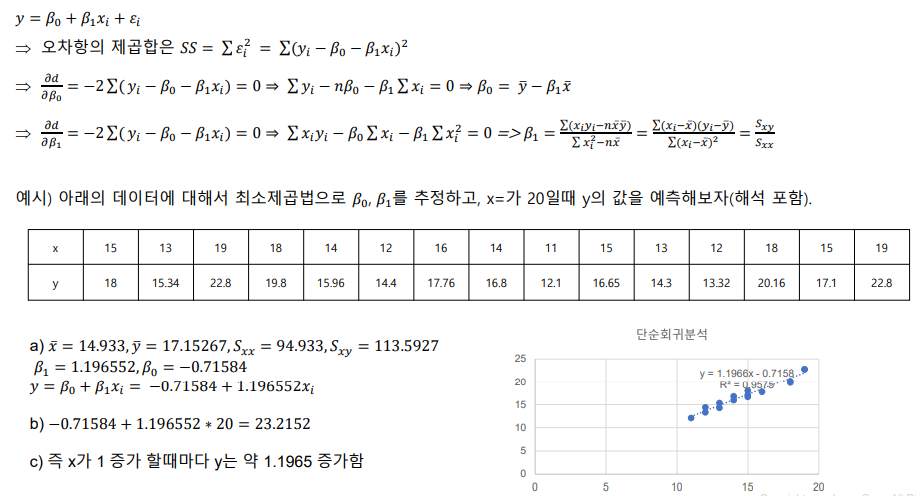
분산분석
- 분산분석을 통한 회귀식의 유의성 판단
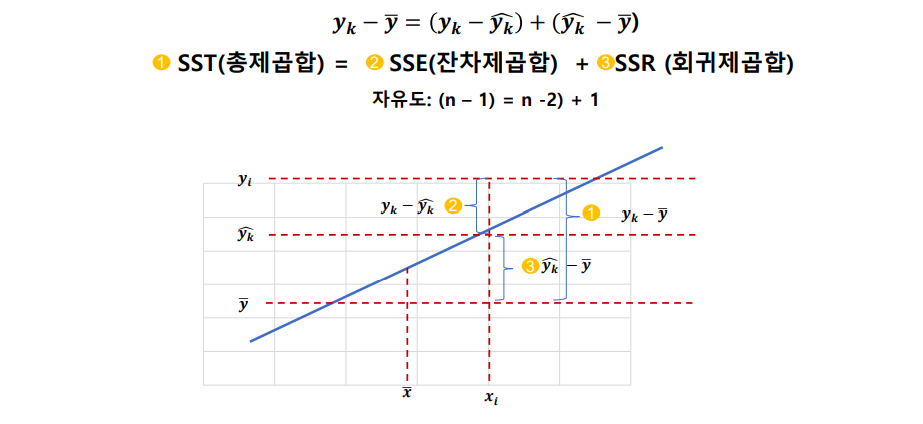
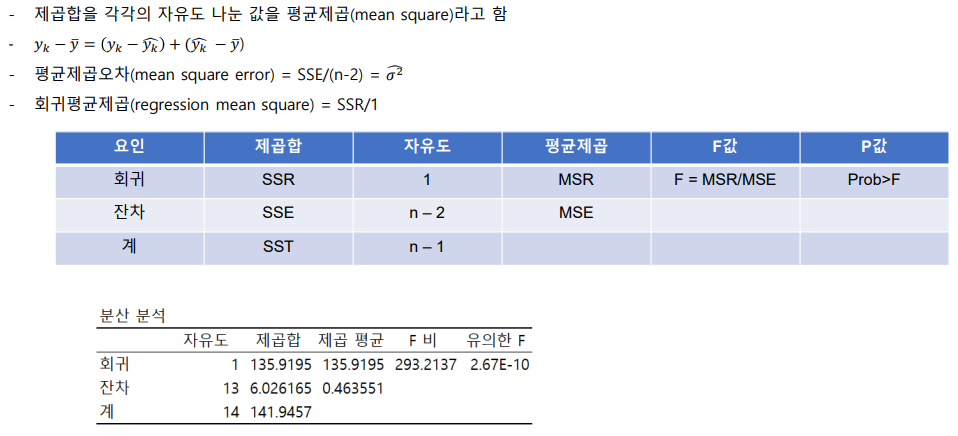
회귀분석의 , 의 추론과 가설검정

결정계수

수정결정계수 Adjust

잔차분석
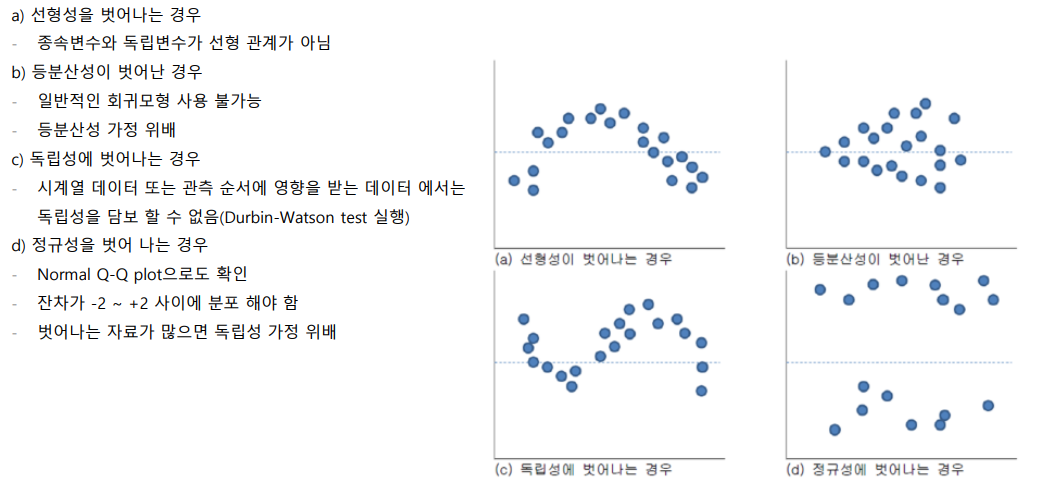
2) 다중회귀분석
- 2개 이상의 독립변수로 종속변수를 예측하는 회귀모형
로지스틱 회귀분석
- 반응 변수가 범주형(이진수)인 경우 사용하는 모형
- ex) 제품불량, 신용도
다항 회귀분석
- 독립변수가 k개이고 반응변수와 독립변수가 1차 함수 이상인 회귀분석
변수선택법
-
전진 선택법(forward selection)
- 독립변수를 1개부터 시작하여 가장 유의한 변수들부터 하나씩 추가하면서 모형의 유의성을 판단하는 방법
-
후진 제거법(backward selection)
- 모든 독립변수를 넣고 모형을 생성한 후, 하나씩 제거하면서 판단하는 방법
-
단계적 선택법(stepwise selection)
- 위의 두가지 방법을 모두 사용하여 변수를 넣고 빼면서 판단하는 방법
더미 변수(dummy variable)
-
값이 ‘0‘ 또는 ‘1’로 이루어진 변수
-
지금까지 회귀분석에서는 연속형 변수를 사용하는 예를 들었지만, 범주형 변수를 사용하기 위해서는 더미변수가 필요함
-
예를 들어 사는 지역을 ‘1’, ‘2’, ‘3’으로 사용하면 연속형 변수여서 정확한 변수로 사용할 수 없음
-
범주형 변수를 0과 1의 조합으로 표현 할 수 있도록 더미 변수를 생성함
-
예시) 최종 학력: 고졸, 대졸, 석사, 박사 4가지로 표현 한다면 필요한 더미의 개수는 4-1 = 3개임
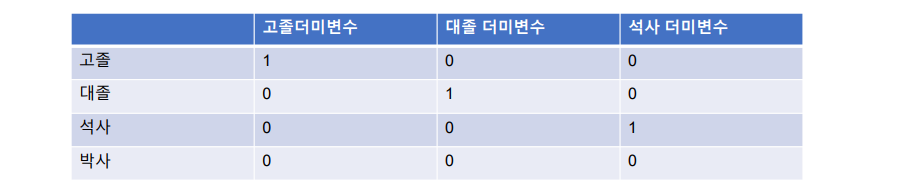
다중공선성(Multicollinearity)
-
상관관계가 높은 독립변수들이 동시에 사용될 때 문제가 발생
-
결정계수 값이 높아 회귀식의 설명력은 높지만 독립변수의 P-value 커서 개별 인자들이 유의하지 않는 경우 의심할수 있음
-
일반적으로 분상팽창요인 (Variance Inflation Factor: VIF)이 10 이상이면 다중공선성이 존재함
-
, k번째 독립변수를 종속변수로 나머지를 독립변수로 하는 회귀모형의 결정계수
-
분석이 매우 커져서 문제발생 또는 독립변수가 종속변수에 끼치는 영향에 문제가 발생
해결 방안
1) 다중공선성이 존재 하지만 유의한 변수인 경우 목적에 따라서 사용할 수 있음
2) 변수 제거
3) 주성분분석으로 변수를 재조합

