✍Ch01_09<테일러 급수>

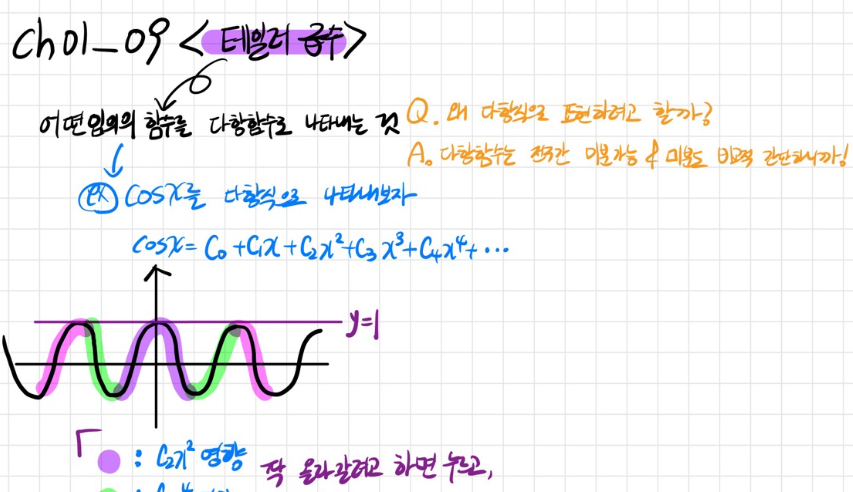
✅테일러 급수가 만들어진 이유, 그래프를 통한 이해

초월함수보다는 다항함수가 다루기 쉽다, 자주 접해왔을 뿐더러 다항함수는 전구간에서 미분도 가능하고 미분도 간단하니까! 그래서 초월함수를 다항함수로 바꿔주는 것이 테일러 급수이다. 테일러 급수가 만들어지는 과정은 코사인 그래프를 통해서 조금 쉽게 생각해볼 수 있다. 형광펜 칠한 부분을 보면 서로 서로 부호가 바뀌며 영향을 주면서 결국에는 무한대로 갔을 때 코사인 함수의 형태를 띄게 된다.

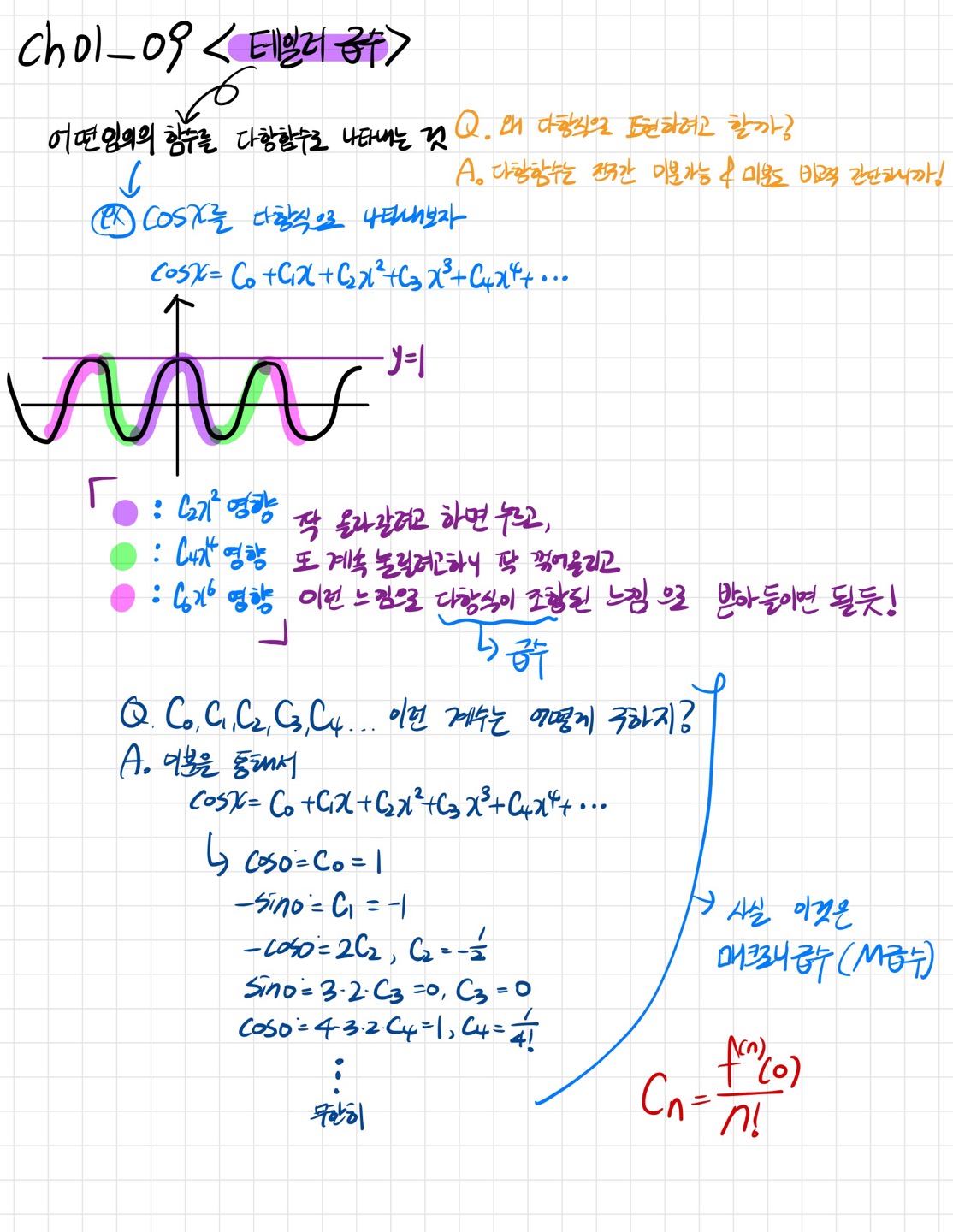
✅테일러 급수와 매크로니 급수의 차이

테일러 급수는 a점이라는 위치를 잡아줄 수 있지만 매크로니 급수는 0을 기준으로 만들어진 놈이다.

✍Ch01_10<스칼라를 벡터로 미분하는 법>

✅좀 더 간결하게 스칼라를 벡터로 미분하기

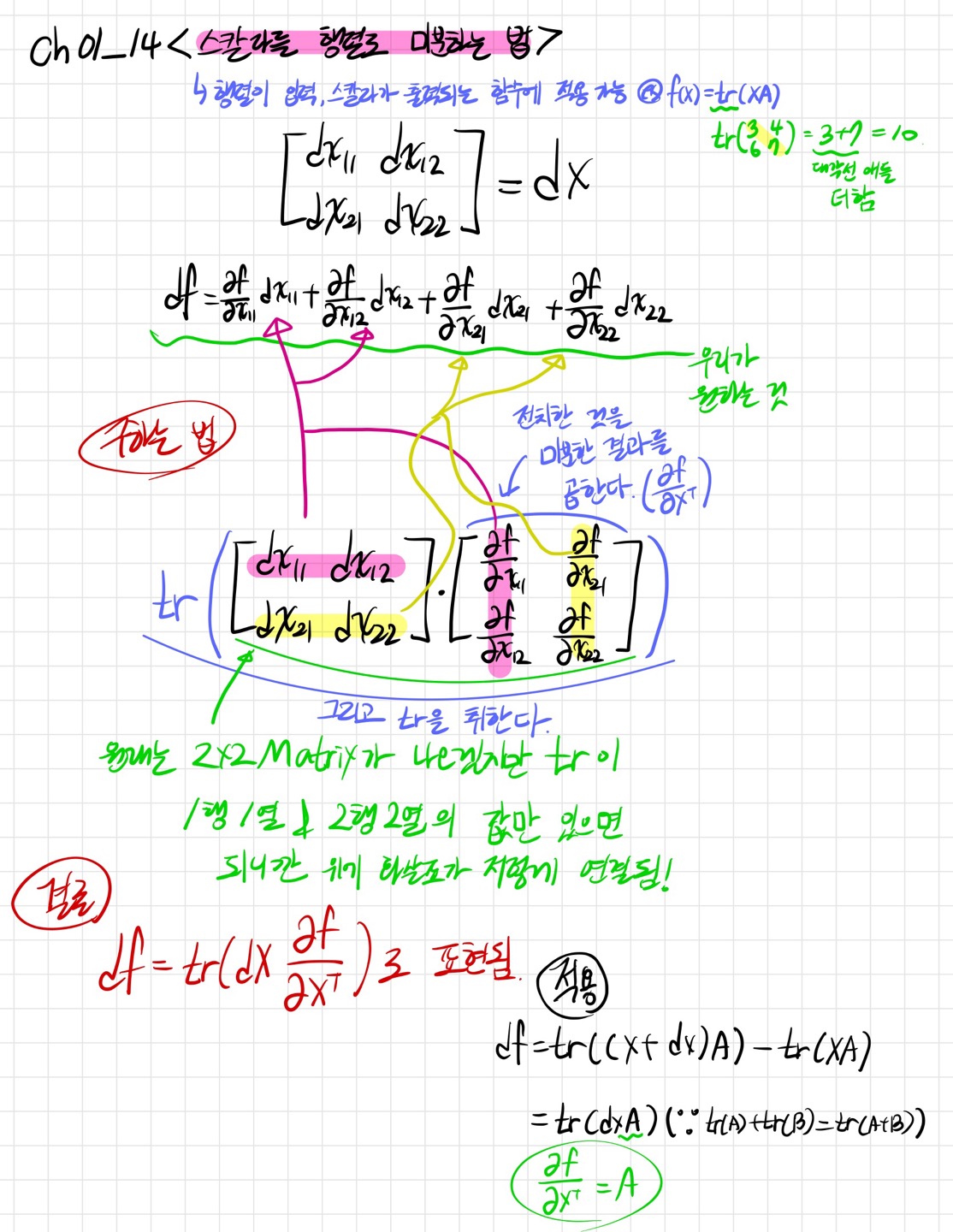
곱미분 법칙을 사용해서 df를 구하면 훨씬 간단하게 구할 수 있다. 변수가 적을 때는 풀어서 편미분도 가능하겠지만 변수가 많아지거나 식이 더 길어진다면 자연스럽게 이 방법으로 오게 되어있다.

✍Ch01_11<왜 그라디언트는 항상 가파른 방향일까>

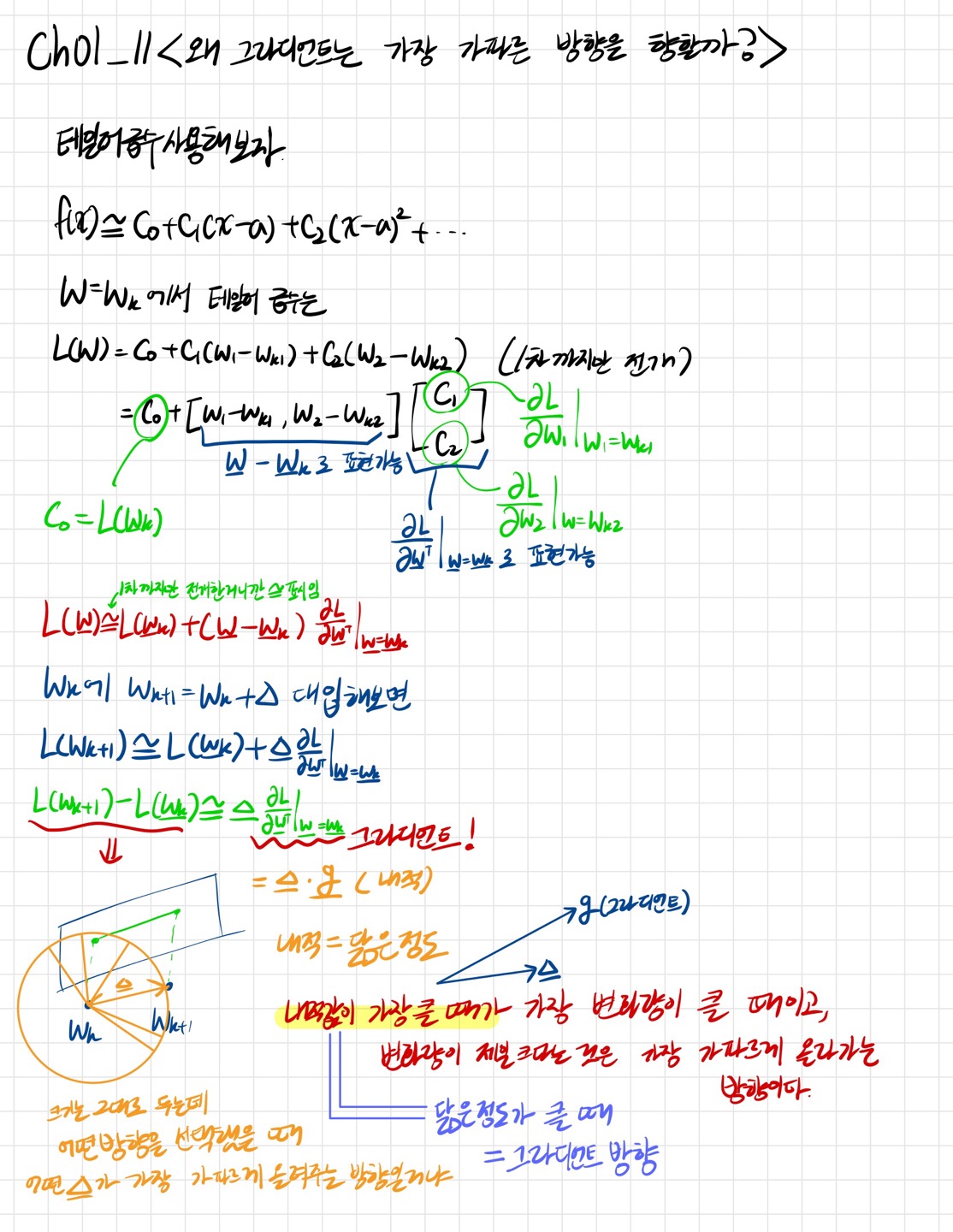
✅앞에서 내적은 닮은정도라고 학습했다.

내적은 닮은 정도라는 것을 이용해서 그라디언트가 왜 항상 가파른 방향인지를 알게되었다. 내적값이 가장 클 때라는 것은 세타가 0도가 된다고 봐야한다. 그때 그라디언트가 가장 가파른 방향이 된다.

✍Ch01_12<벡터를 벡터로 미분하는 법>

✍Ch01_13<벡터를 벡터로 미분할 때에 연쇄법칙>

✍Ch01_14<스칼라를 행렬로 미분하는 법>

✍Ch01_15<행렬을 행렬로, 벡터를 행렬로 미분하는 법>

<출처: 패스트캠퍼스 혁펜하임의 AI DEEP DIVE(ONLINE.) Ch01_09~15>