✍Ch01_04<전치와 내적>

✅전치의 뜻

기존의 행렬에서 행과 열을 바꾸는 것이다.

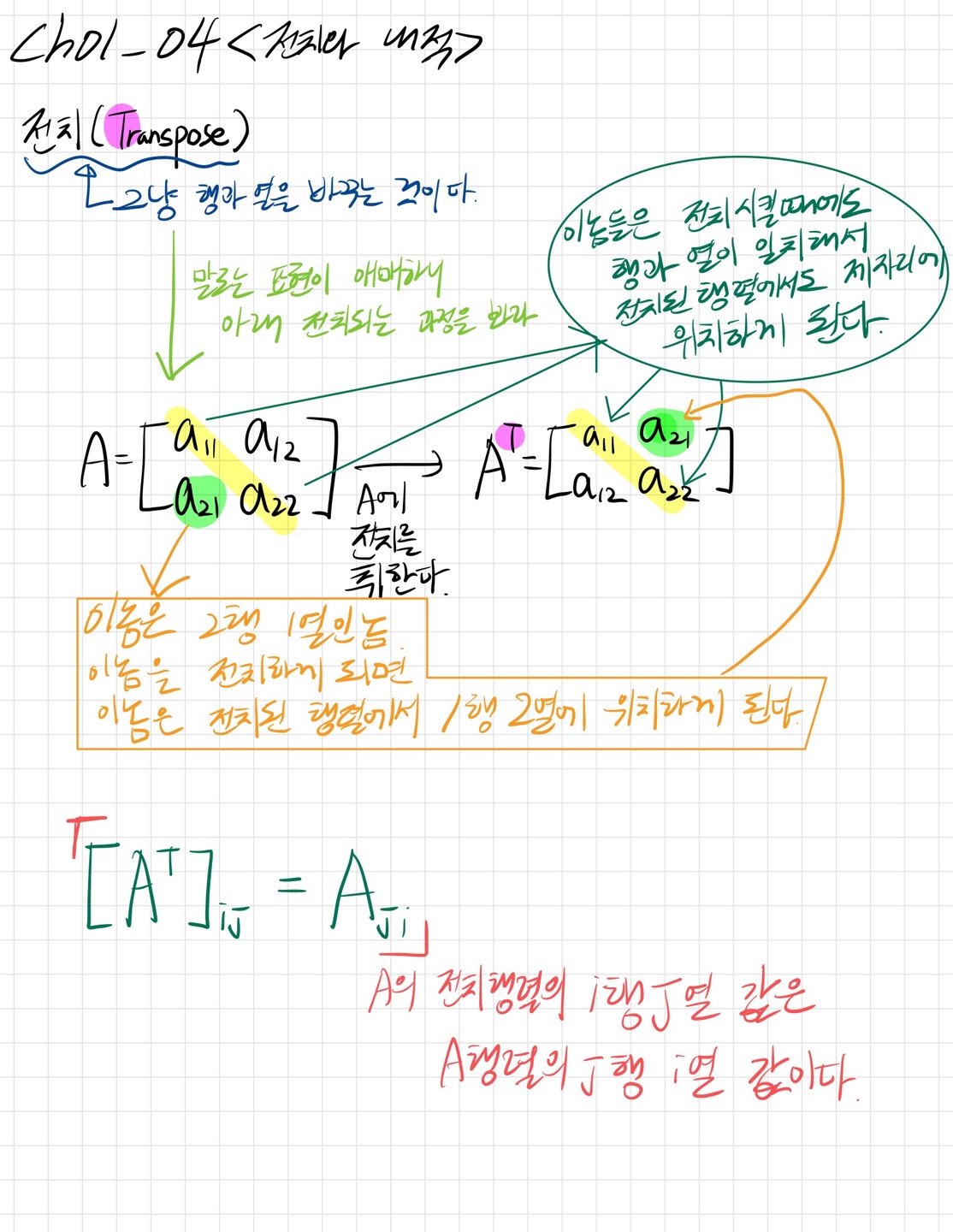
✅ 적용

강의에서는 변수로만 식을 알려주셔서 강사님을 못믿는 것은 아니지만 정말 전치를 취했을 때의 식이 변환되는지 숫자를 통해 확인해보았습니다!

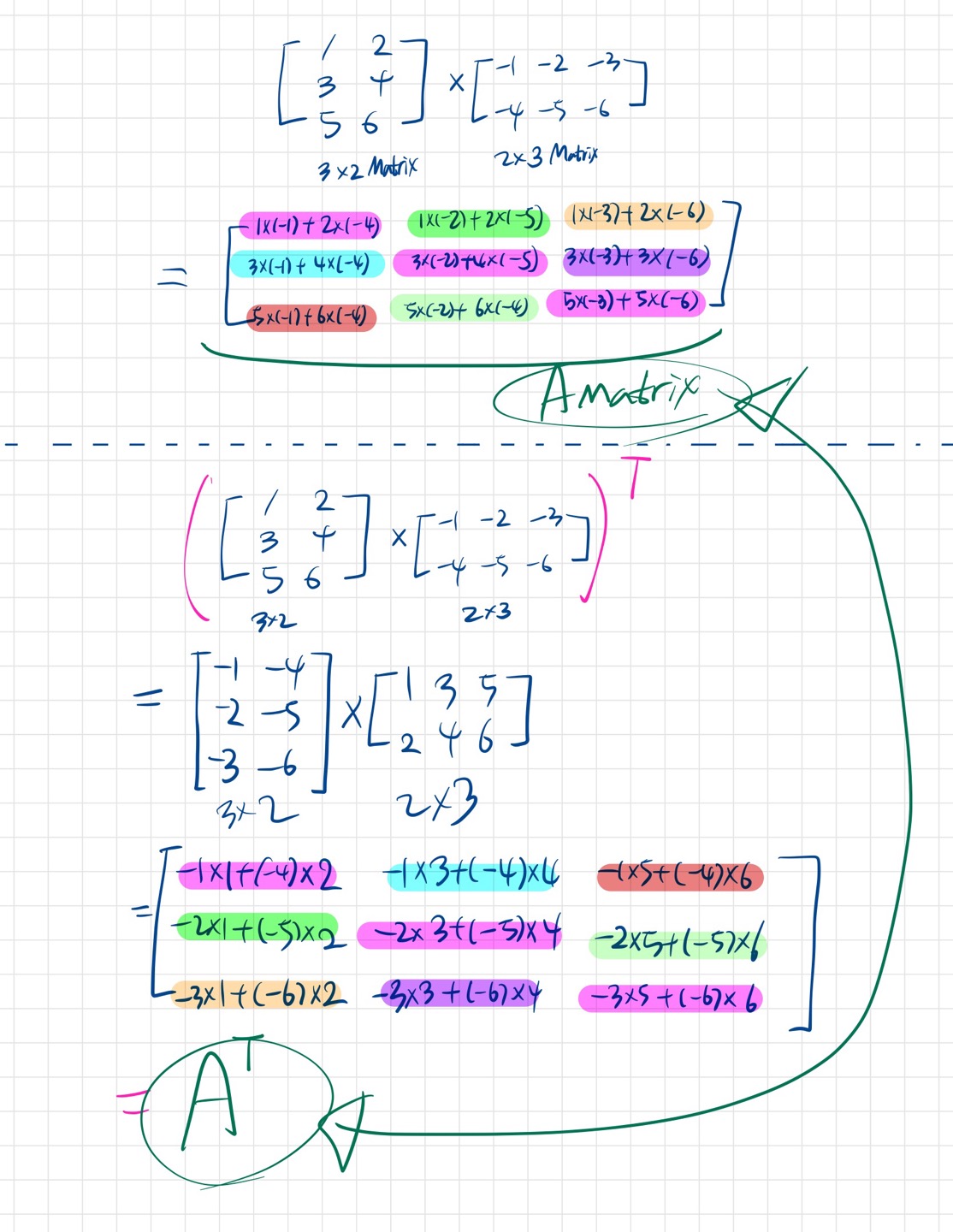
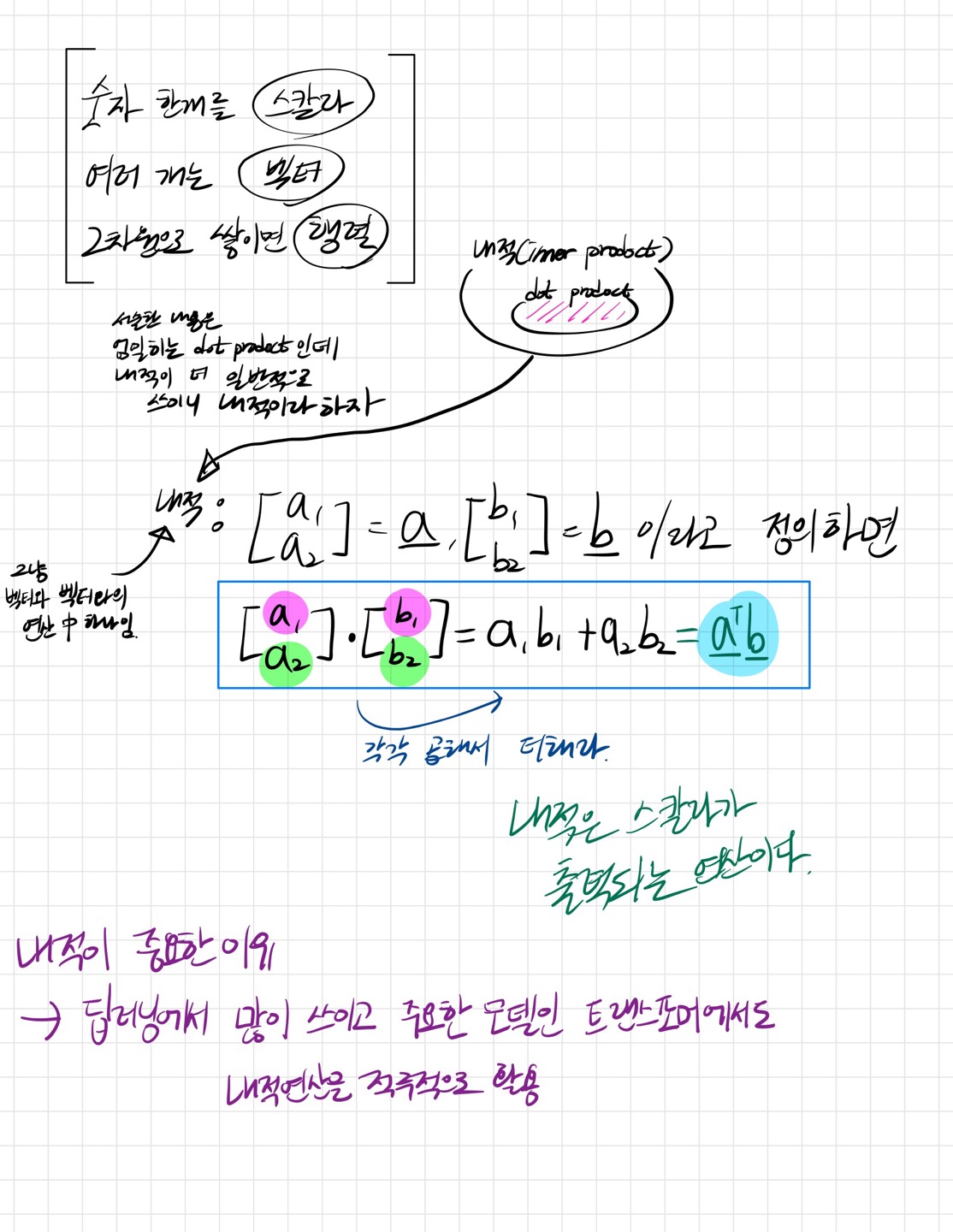
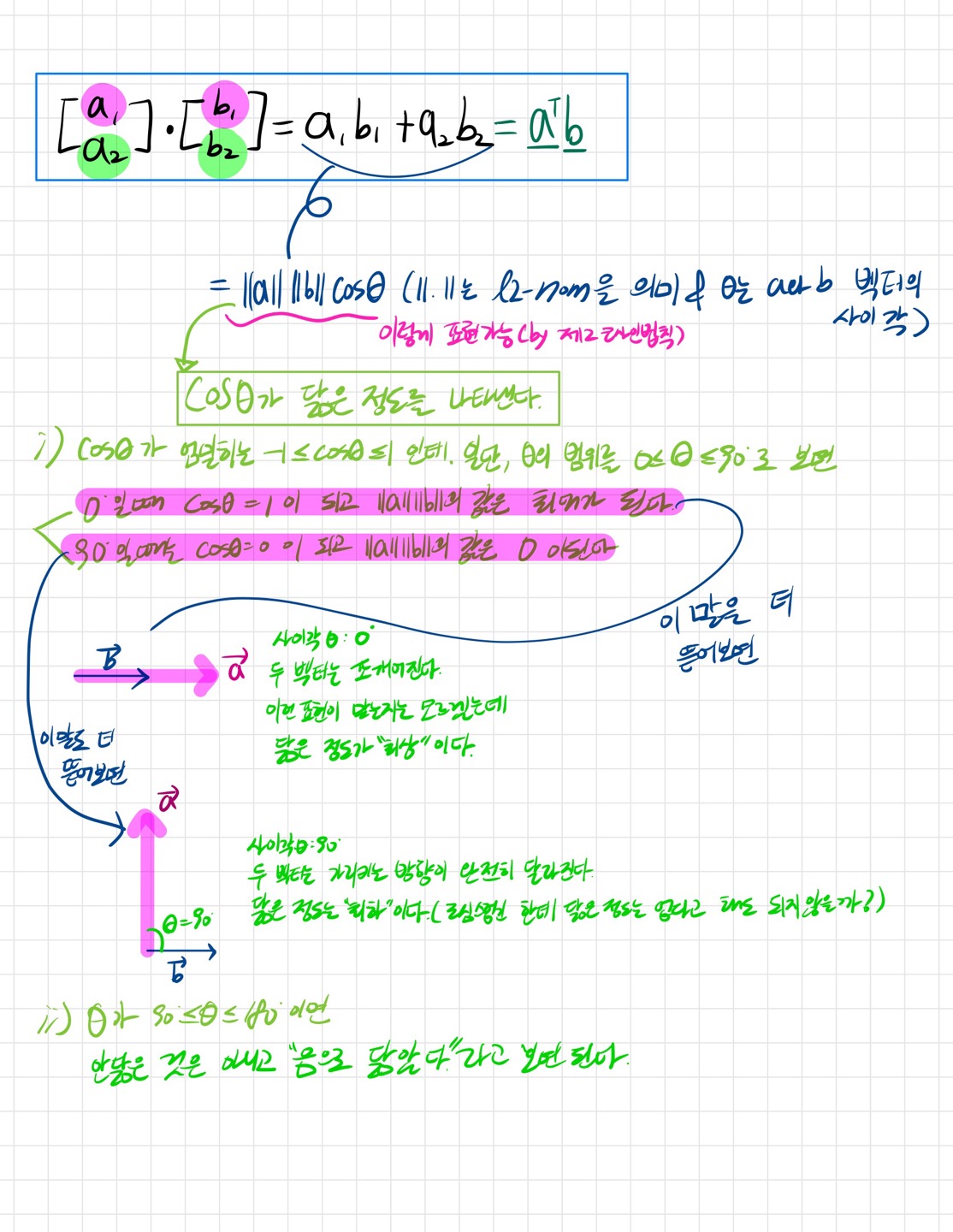
✅ 내적은 행렬의 곱셈과 다르다

처음에 강의를 들으면서 뭐지 뭐지 했던 부분이였다. 내적을 행렬의 곱셈과 착각하면서 혼란스러웠는데, 내적은 벡터와 벡터와의 연산이다!

✅ 닮은 정도

코사인 세타가 두 벡터간의 닮은 정도를 나타낸다!

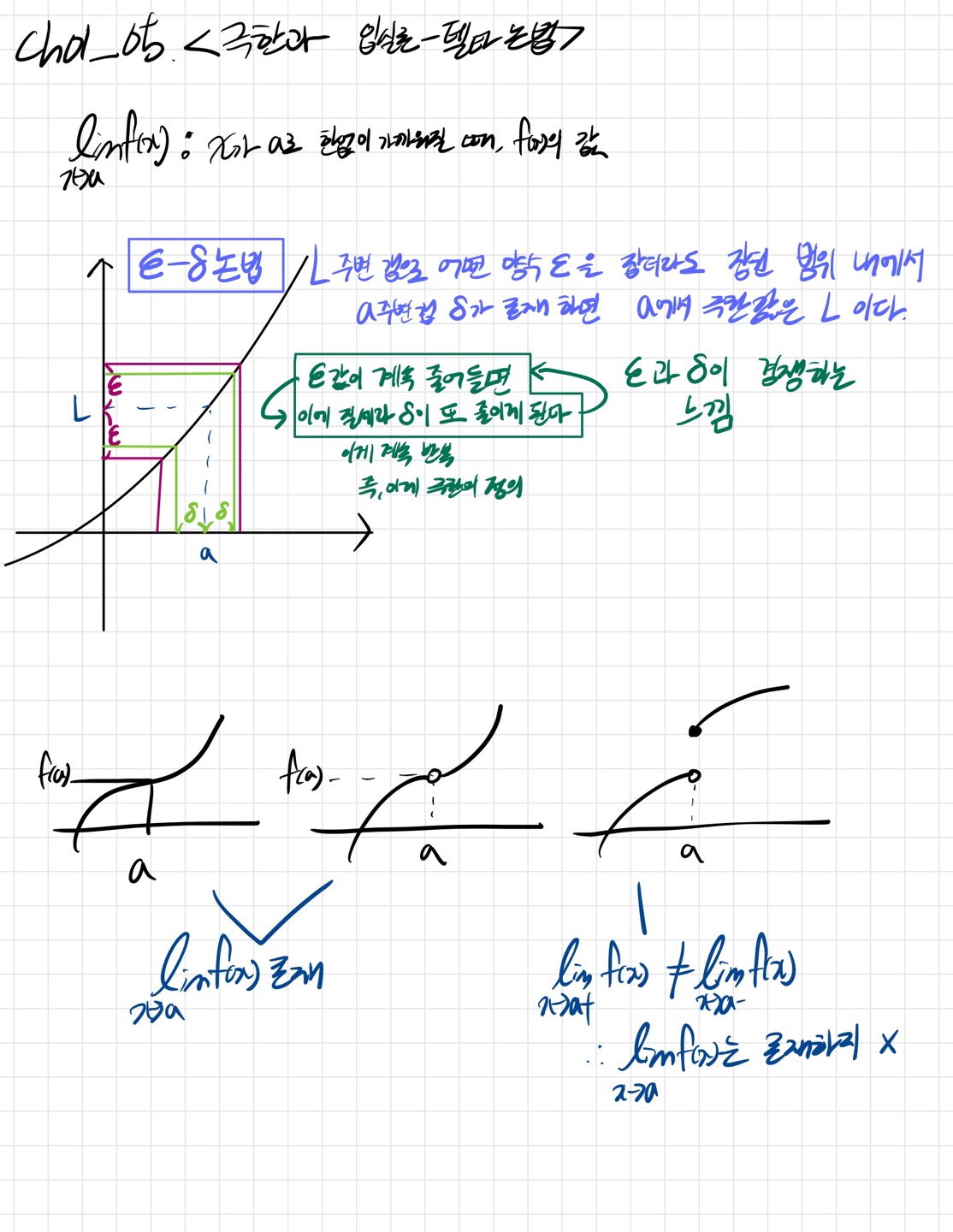
✍Ch01_05<극한과 입실론-델타 논법>

✅ 입실론과 델타의 경쟁

입실론과 델타가 서로 경쟁을 한다는 느낌으로 받아들이면 극한의 개념을 쉽게 이해 가능

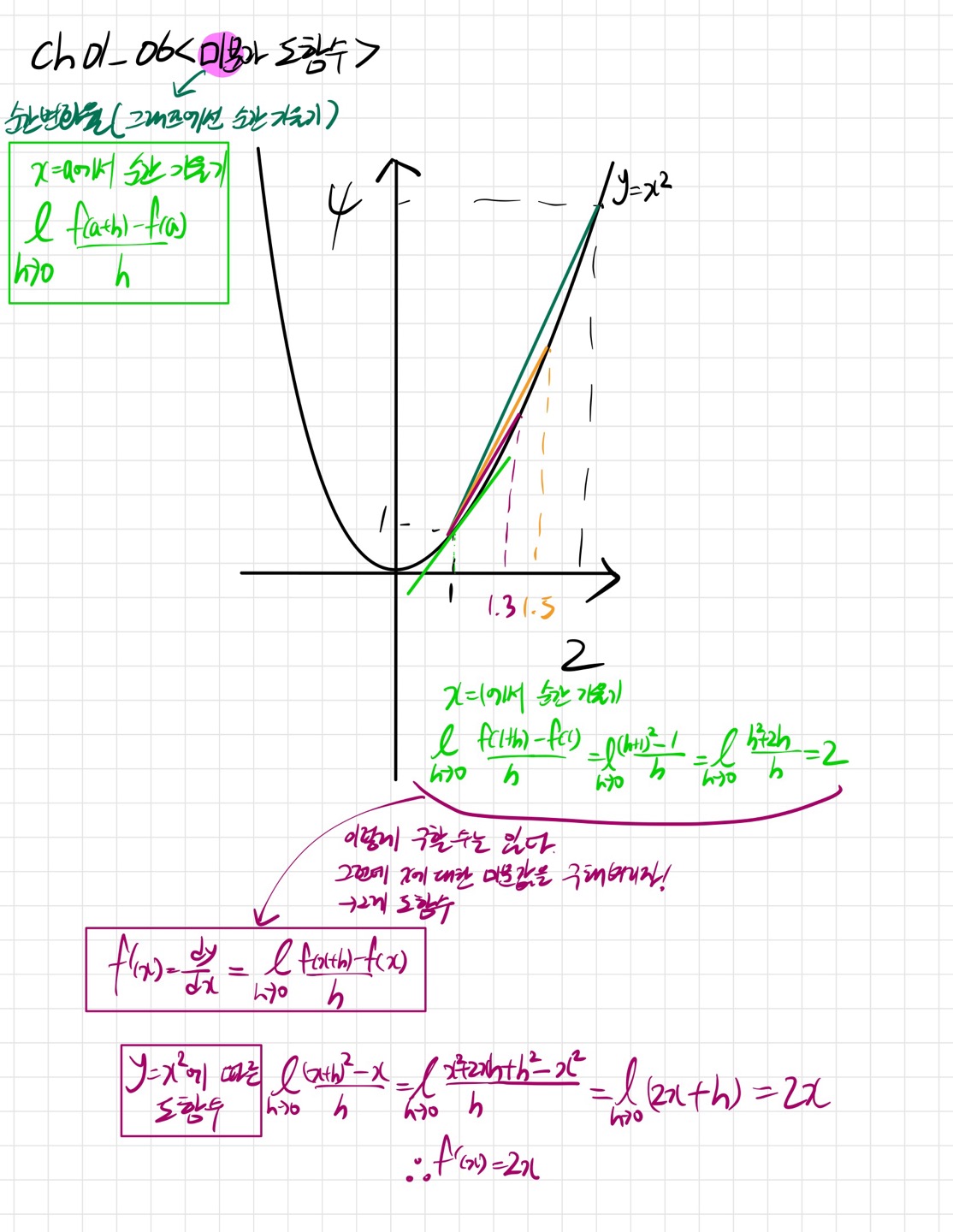
✍Ch01_06<미분과 도함수>

✅살짝은 과장된 그림

이해를 돕기위해 그림을 과장되게 그렸습니다. 즉, 한점을 고정시키고 다른 점에서 점점 고정시킨 점으로 오게되면 그때의 기울기가 순간 기울기가 됩니다.

✅딥러닝에서 자주 보이는 도함수

기본적으로 한 번씩 체크하고 넘어가자!

✍Ch01_07<연쇄법칙>

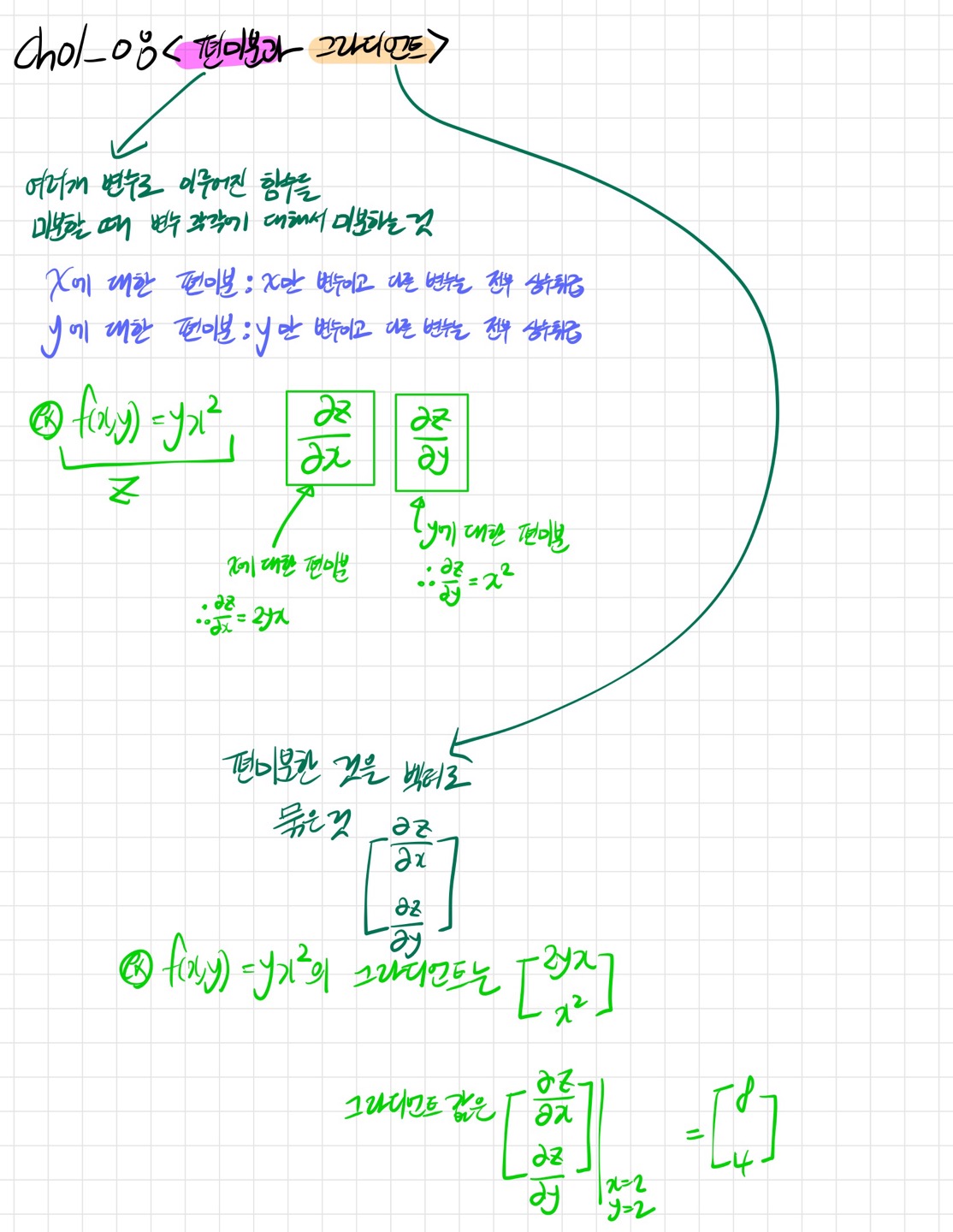
✍Ch01_08<편미분과 그라디언트>

✅그라디언트

편미분된 값을 벡터로 표현한 것이 그라이언트!

<출처: 패스트캠퍼스 혁펜하임의 AI DEEP DIVE(ONLINE.) Ch01_04~08>