Analyzing Feed-Forward Blocks in Transformers through the Lens of Attention Maps

잘못된 내용이 있다면 댓글 부탁드립니다!! 감사합니다 :)

Motivation: 기존 방식들은 FF 네트워크 까지 통합하지 않음.
Summary: 전체 Layer를 이용해 input 과 output의 관계를 확인하는 방법
Novelty: non-linear function 로 decompose가 안되었던 문제에 대한 해결방안 제시
ICLR 2024 spotlight
https://openreview.net/forum?id=mYWsyTuiRp

용어

Input Contextualization: 입력 데이터가 주어진 맥락 내에서 어떻게 해석되고 사용되는지를 의미한다.

Introduction, Background

input contextualization (맥락과 과련짓다) 의 feed-forward (FF) blocks에서의 영향을 분석한 논문(component-by-component through the lens of attention maps)이다. FF 에서 rendering 을 통해 attention map을 만들어 시각화해 보인다.

interpretation scheme의 장점

1. attention mechanisms are spread out in the entire Transformer architecture; 하나의 component 는 semi-transparent window가 되고 전체를 모아서 보면 internal processing 을 볼 수있다.
2. token과 token의 관계는 인간이 보기에 더 익숙하다. 모델에서 high-dim으로 나오는 representation을 직접적으로 관찰 가능해진다.
3. input attribution은 모델 예측 설명에 중요한 요소..?
4. attention map refinment 적인 접근 방식을 통해 더 나은 attribution을 추정할 수 있다. (gradient based 방식에 비해서)

본 논문에서는 input contextualization 의 영향을 확인하고, norm-based 분석을 확장해 FF 처리 과정을 반영하는 attention maps을 계산하는 방식을 제안한다.

norm based 분석은 gradient 방식보다 몇가지 장점이 존재한다.
: the impact of input (∥x∥) is considered unlike the vanilla gradient, and that only the forward computation is required. 원래 norm based 방식은 FF에서 간단하게 적용될 수 없었지만 본 연구에서 해당 limitation을 다룬다. 이를 통해서 information geometric perspectives 로부터 input contextualization을 다룰 수 있게 된다.

Attention map: 본 논문에서는 attention map의 분석 범위를 FF 블록과 residual connection 그리고 layer normalization 까지 포함한다. 저자는 norm 기반 분석 및 integrated gradient를 사용해 각 요소의 기여도를 attention map에 decompose한다. 이를 통해 구성요소가 input contextualization 에 미치는 영향을 시각화 한다.

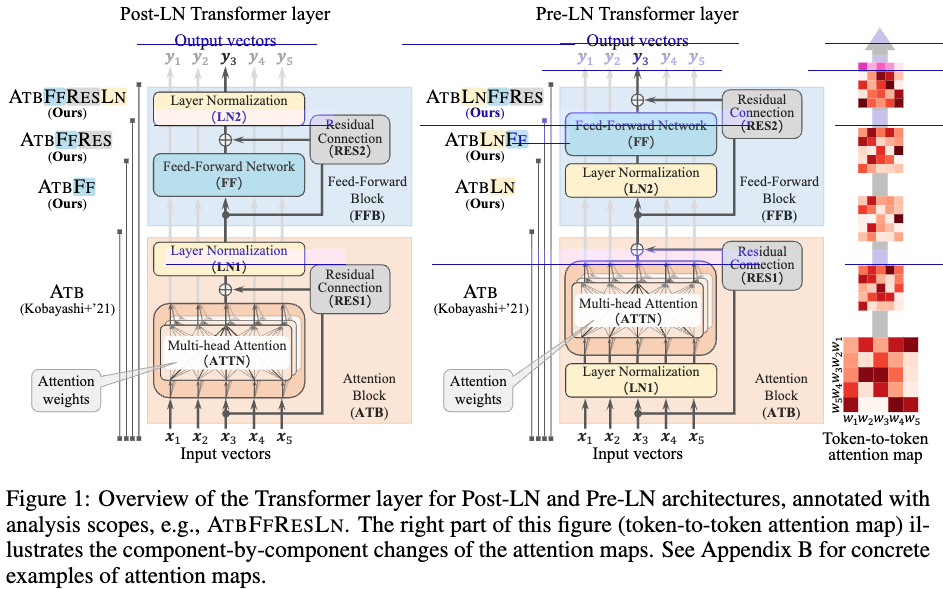
기존 연구에서는 norm-based analysis방식을 통해 attention map ($x_i$가 $y_j$를 만드는데 얼마나 큰 기여를 했는지 볼 수 있게 하는 도구) 을 만든다. 이때 아래 6, 7 번 수식이 ATB의 과정을 설명이고 $||F_i^{ATTN}(x_j;X)||$ 를 기존의 $\alpha _{i,j}$ 대신 사용해 서 attention map을 만든다.

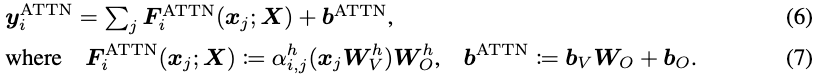
본 논문에서는 transformer layer 전체를 바탕으로 분석을 진행한다.

the norm $∥F_i^{ATB} (x_j ; X)∥$ was analyzed to quantify how much the input x_j impacted the computation of the output $y^{ATB}_i$ through the ATBs. → $∥F^{Layer}_i (x_j ; X)∥$

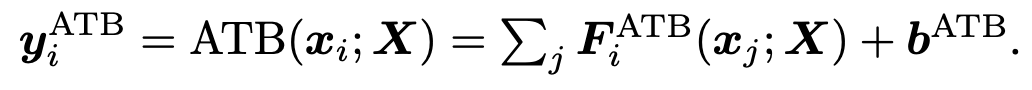
Proposal Method: Analyzing FFBs through Refined Attention Map

Difficulty to incorporating FF: FF의 non-linear 인해 decomposing이 불가능해진다는 challenge가 남아있었다.

Integrated Gradients (IG): deep learning에서 NN 해석하는데 사용한다. integral과 gradient 연사을 통해 각 input feature가 output에 얼마나 기여하는지 확인할 수 있다. IG 의 contribution (attribution) score 는 다음과 같이 구할 수 있다.

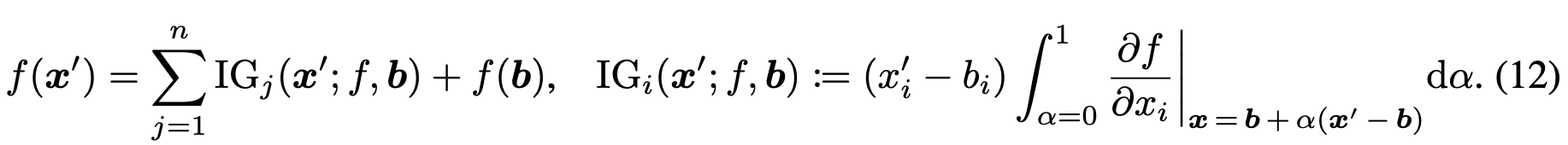
b 는 contribution score 추정을 위해 사용되는 baseline vector이다.

Expansion to FF: $\tilde{g} : \mathbb{R}^n → \mathbb{R}$ is defined as $\tilde{g}(x_1, . . . , x_n) := g(x_1 + · · · + x_n)$ 변형을 통해서 input 을 single scalar로 표현해 버린다. 그리고 element-level activation $g: \mathbb{R} \rightarrow \mathbb{R}$, h는 얼마나 특정인풋이 아웃풋에 기여했는지를 나타내게 한다.

Expansion to entire layer:

$∥h_j (F^{Pre g}_i(x1), . . . , F^{Pre g}_i (x_n); \tilde{g}, 0)W_2∥$로 계산된 input $x_j$에 대해 i 번째 FF 로 기여도를 볼 수 있고, 분해된 (decomposed) ATTN, RES, LN layer를 kobayashi et al 이 사용한 방식으로 결합할 수 있다.