알고리즘
1.선택 정렬(Selection Sort)

선택 정렬 매번 가장 작은 것을 찾아 제일 앞의 값과 교환하는 것 데이터가 무작위로 여러 개 있을 때, 이 중에서 가장 작은 데이터를 선택해 맨 앞에 있는 값과 교환하고, 그다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복수행 시간복잡도 선택정
2.삽입 정렬(Insertion Sort)
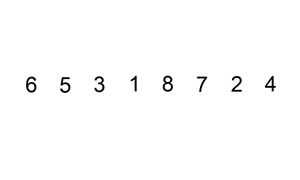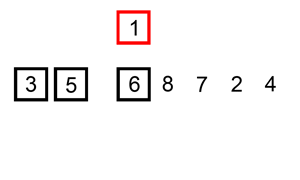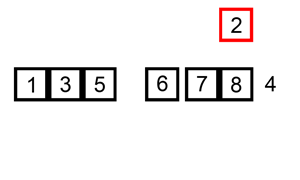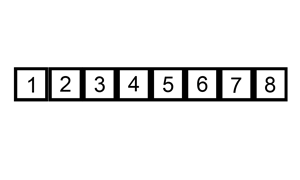
데이터를 하나씩 확인하며, 각 데이터를 적절한 위치에 삽입하여 정렬필요할 때만 위치를 바꾸므로 '데이터가 거의 정렬되어 있을 때' 훨씬 효율적선택 정렬은 현재 데이터의 상태와 상관없이 무조건 모든 원소를 비교하고 위치를 바꾸지만 삽입 정렬은 그렇지 않다자신보다 작은 값
3.퀵 정렬(Quick Sort)

퀵 정렬 정렬 알고리즘 중 가장 많이 사용되는 알고리즘. 퀵 정렬만큼 빠른 알고리즘에는 "병합 정렬" 알고리즘이 있으며 이 두 알고리즘은 대부분의 프로그래밍 언어에서 정렬 라이브러리의 근간이 되는 알고리즘이다. pivot(기준 데이터)를 설정하고, 그 기준보다 큰 데이
4.JS 알고리즘 입출력, 메서드, 에러

fs : File System 모듈 readFileSync : 파일을 읽고 난 후에 실행(동기 처리) stdin : 표준 입력 파일('dev/stdin' 은 stdin 의 경로, 시스템에 따라 변경될 수 있음 toString() : 읽어서 가져온 반환값은 Buffer
5.버블 정렬(Bubble Sort)

버블 정렬은 매우 간단한 정렬이지만 어떻게 설정하느냐에 따라서 수행횟수가 달라질 수 있다. 매번 수행될때마다 마지막에 위치한 배열의 원소가 정렬된다는 특징을 갖는다. 첫번째 방식은 위 특징을 고려하지 않고 매번 수행때마다 처음부터 끝까지 모두 비교한 방법이다. 두번째
6.DFS

dfs의 풀이방법은 2가지(재귀, 스택)이다. 그래프 간선 정보가 오름차순으로 정렬되어 있다는 가정 하에, **재귀 -> 인접한 노드 중 작은 노드 번호 우선 dfs 탐색 (부모 -> 왼쪽 -> 오른쪽) **스택 -> 인접한 노드 중 큰 노드 번호 우선 dfs 탐색 (
7.BFS

큐를 사용하는 것보다 deque 를 이용해 큐처럼 사용하는게 편하다.방법왼쪽에서 입/출력: appendleft(val), popleft()오른쪽에서 입/출력: appeend(val), pop()(오른쪽에서의 입/출력이 기본이고 왼쪽인 경우 'left' 가 붙는다.)
8.Dynamic Programming (동적 계획법)

하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용(재활용)일반적인 재귀보다 훨씬 효율적인 계산이 가능하다. 일반적인 재귀는 다음과 같이 동일한 계산들이 반복되는 경우가 많다그러나 dp를 사용하면 이전에 계산한 값들을
9.이분 탐색/이진 탐색(Binary Search)

이분 탐색(이진 탐색)은 정렬되어 있는 절반씩 탐색 범위를 좁혀가며 데이터를 탐색하는 방법이다. 이분 탐색은 데이터가 정렬되어 있어야만 사용할 수 있다.이분 탐색은 반복문과 재귀를 이용해 구현할 수 있다.이분 탐색은 일반적으로 찾고자 하는 값을 발견한 후 바로 종료하게
10.파라메트릭 서치(Parametric Search)

이분 탐색이 정렬된 배열에서 값의 위치를 찾거나 존재 유무를 파악하는데 사용된다면, 파라메트릭 서치는 정렬된 배열에서 조건을 만족하는 "최적의 값"을 찾는데 사용된다. 파라메트릭 서치는 주로 특정한 조건을 만족하는 최소 또는 최대의 값을 찾는 데 사용된다.이분 탐색은
11.그리디 알고리즘 (Greedy Algorithm)

그리디 알고리즘 (Greedy Algorithm) Greedy 는 '탐욕스러운, 욕심 많은' 이란 뜻이다. 탐욕 알고리즘은 말 그대로 선택의 순간마다 당장의 눈앞에 보이는 최적의 상황만을 쫒아 최종적인 해답에 도달하는 방법이다. 당장 눈앞에 보이는 최적의 상황만을 쫒
12.트리

정의등...
13.이진 검색 트리

정의관련 문제를 통한 풀이 예시 등 5639
14.DP 방식에 따른 시간/메모리 사용량 차이 분석

어떤 문제에서 다음과 같은 점화식이 주어졌다고 가정한다.dpn = dpn // p + dpn // q (단, dp0 = 1)일반적으로 이를 해결하기 위해 DP 배열을 생성하여 dpn 값을 구하는 방식이 사용된다. 하지만 이 문제에서는 n의 범위가 매우 크기 때문에, 단
15.플로이드-워셜 알고리즘

플로이드-워셜 알고리즘 플로이드-워셜(Floyd-Warshall Algorithm)은 그래프에서 가능한 모든 노드 쌍에 대해 최단 거리를 구하는 알고리즘이다. 시간 복잡도는 이다. 다익스트라 알고리즘과 달리 모든 노드 쌍에 대해 최단 거리를 구하고, 음의 가중치를 가
16.LIS (이진 탐색 기반)
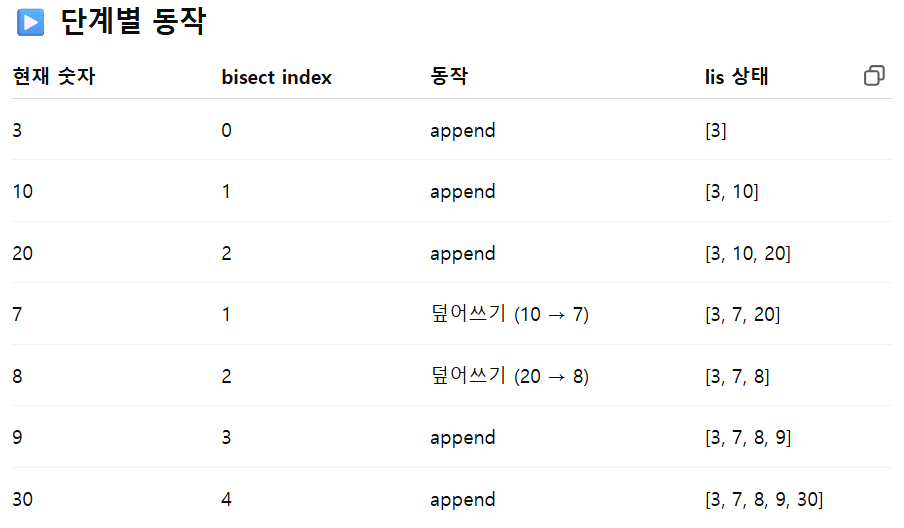
가장 긴 증가하는 부분 수열(LIS)의 길이를 O(nlogn) 시간에 구할 수 있는, 이진 탐색 기반 LIS 알고리즘에 대해 정리하였다.1\. lis 리스트를 하나 만든다이 리스트는 실제 LIS 수열이 아닌, 길이를 추적하기 위한 도구이다 (실제 정답 LIS 수열과의
17.LIS (DP 기반, 역추적 포함)

수열이 주어졌을 때, 가장 긴 증가하는 부분 수열(LIS, Longest Increasing Subsequence)을 DP(Dynamic Programming, 동적 계획법)를 이용해 풀이하는 방법을 설명한다.각 원소를 끝으로 하는 증가하는 부분 수열의 최대 길이를 저
18.Union-Find 알고리즘

유니온 파인드Union 연산 - 두 그룹을 합치는 연산Find 연산 - 원소가 속해 있는 그룹을 알아내는 연산방식 1원소별로 그룹의 번호를 배열로 가짐=> 초기값은 자신의 번호(1부터로 가정)=> 이 방식의 경우 그룹 B를 그룹 A에게 합치는 경우B의 원소 값과 동일한
19.MST 에 대한 고찰

간선의 비용을 작은 것부터 합치는데, 이 과정에서 사이클 여부를 확인하기 위해 union-find 가 사용되는 것즉, 그리디를 메인으로 사이클 여부 확인용으로 union-find 를 쓰는 것by 혜역
20.Dijkstra (다익스트라)

다익스트라 알고리즘은 그래프 간선정보(단/양방향 상관X)가 주어졌을 때 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘이다. 그러나 거리가 음수인 경우에는 사용할 수 없다. 해당 경우에는 벨만 포드 알고리즘을 사용해야 한다.
21.순열, 조합

순열 첫째 줄에 전체 원소 개수 N, 뽑을 원소 개수 R 둘째 줄에 배열 정보가 주어질 때, 가능한 순열, 중복 순열 경우를 모두 출력하는 코드이다. *핵심은 perm 함수의 매개변수가 depth(길이)를 뜻한다는 것을 알아야 한다. 자바 중복 순열 위 코드에서 v