DP 방식에 따른 시간/메모리 사용량 차이 분석

문제 소개

어떤 문제에서 다음과 같은 점화식이 주어졌다고 가정한다.

dp[n] = dp[n // p] + dp[n // q] (단, dp[0] = 1)

일반적으로 이를 해결하기 위해 DP 배열을 생성하여 dp[n] 값을 구하는 방식이 사용된다. 하지만 이 문제에서는 n의 범위가 매우 크기 때문에, 단순한 bottom-up 방식으로는 시간 초과 혹은 메모리 초과가 발생할 수 있다.

1. 일반적인 Bottom-up 방식

dp = [1]
for i in range(1, n+1):
    dp.append(dp[i//p] + dp[i//q])
print(dp[n])

• dp[1]부터 dp[n]까지 모두 구함.
• 시간 복잡도: O(n)
• 메모리 사용량: O(n)
• ✔ 단순하지만 ❌ 연산 수와 메모리 모두 비효율적

2. 최적화된 Bottom-up 방식

v1, v2 = n // p, n // q
mv = max(v1, v2)
for i in range(1, mv+1):
    dp[i] = dp[i//p] + dp[i//q]
print(dp[v1] + dp[v2])

• dp[n//p], dp[n//q]까지만 계산하여 연산을 줄임.
• ✔ 시간은 줄었지만 ❌ 여전히 불필요한 값들도 포함됨.
• ❗ 실제로 dp[v1]과 dp[v2]를 구하는 데 모든 1 ~ mv 값이 필요한 건 아님.

3. Top-down 방식 (Memoization)

dp = {0: 1}
def topDown(i):
    if i in dp:
        return dp[i]
    dp[i] = topDown(i//p) + topDown(i//q)
    return dp[i]
print(topDown(n))

• 실제로 필요한 값만 재귀적으로 계산
• 중복 계산은 메모이제이션으로 방지.
• ✅ 연산 수, 메모리 사용량 모두 가장 효율적
• ✔ 불필요한 dp 값 생성을 방지함.

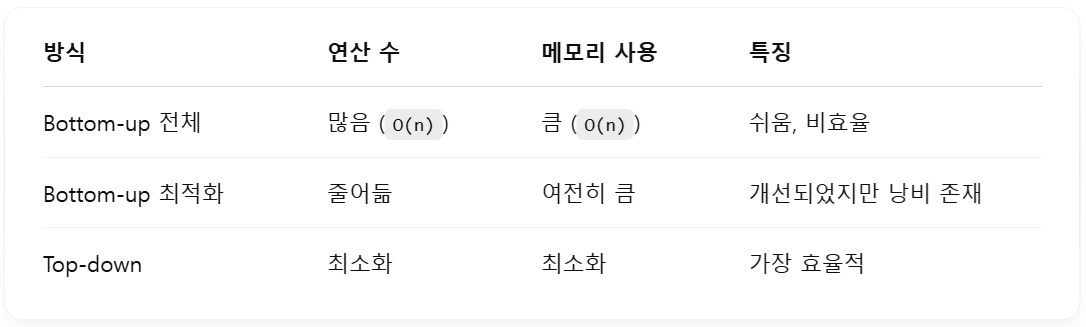
비교 정리

🔍 깨달은 점

• DP 문제라 하더라도 무조건 bottom-up 방식이 좋은 건 아니다.
• 불필요한 값 계산이 많은 경우, top-down 방식이 메모리와 시간 모두 효율적일 수 있다.
• 특히 dp[n] = dp[n//p] + dp[n//q] 와 같이 계산 경로가 log 수준으로 줄어드는 경우, top-down 방식이 압도적이다.