가장 긴 증가하는 부분 수열(LIS)의 길이를 O(nlogn) 시간에 구할 수 있는, 이진 탐색 기반 LIS 알고리즘에 대해 정리하였다.
아이디어
1. lis 리스트를 하나 만든다
이 리스트는 실제 LIS 수열이 아닌, 길이를 추적하기 위한 도구이다 (실제 정답 LIS 수열과의 길이는 같지만, 실제 값은 다를 수 있다.)
2. 각 원소마다 이진 탐색으로 삽입 위치(index)를 찾는다.
-> bisect_left(lis, num) 사용
bisect_left(arr, x) vs bisect_right(arr, x) 비교
- bisect_left(arr, x) -> x 이상인 값이 처음 나오는 위치(index) 반환
- bisect_right(arr, x) -> x 초과인 값이 처음 나오는 위치(index) 반환
*만약 bisect_left(arr, x) 또는 bisect_right(arr,x) 를 사용했을 때, x 이상(또는 초과)인 값이 없다면 결과는 배열의 길이(len(arr))가 된다. 즉, x를 맨 끝에 넣어야 한다는 뜻이다.
3. 두 가지 경우의 수
index == len(lis)-> num 을 뒤에 append()
-> 증가하는 수열의 길이가 늘어남index < len(lis)-> lis[index] = num 으로 덮어씀
-> 길이는 유지하되, 더 작은 값으로 교체 (뒤에 더 많은 수가 붙을 수 있도록 함)
"지금 이 숫자는 뒤에 붙일 수는 없지만, 중간 어딘가를 대신해서 수열의 길이가 증가할 수 있는 가능성을 넓혀줄 수 있으니, 그 자리를 차지하도록 하자"
(덮어쓰기 방식으로 나중에 더 긴 수열이 만들어질 수 있는 예시)
수열 arr = [3, 10, 20, 7, 8, 9, 30]
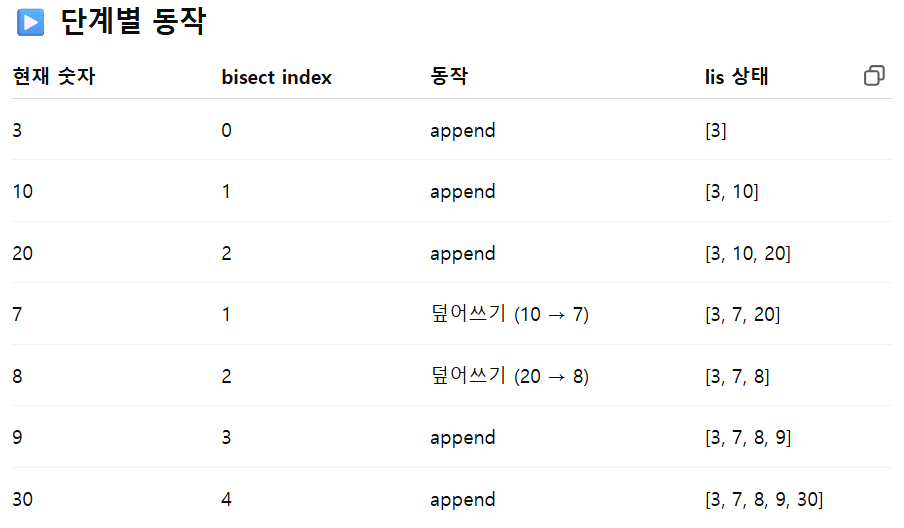10을 7로, 20을 8로 덮어씌우고, 그리고 8 뒤에 9, 30을 붙이면서 결국 길이 5짜리 수열을 만들 수 있게 된다.
덮어쓰는 이유는 지금 당장은 길이가 그대로지만, 작은 숫자로 바꿔놓으면 그 뒤에 더 많은 수가 붙을 수 있는 가능성이 높아진다. 이는 결국 더 긴 LIS 로 이어질 수 있는 가능성이다.
그러나, 이렇게 구해진 lis 배열은 겉보기에는 정확한 LIS 수열처럼 보이지만, 이는 항상 그런 건 아니다. 위 lis 배열은 단순히 길이 5짜리 증가 수열이 존재함을 보장하는 길이 추적용 도구일 뿐이다. 이 알고리즘의 목적은 수열을 정확히 만드는 것이 아니라, 최장 길이를 빠르게 O(nlogn) 계산하는 것이다. 따라서 우리는 이 알고리즘을 통해서는 lis의 최장 길이만을 알 수 있다.
4. 최종적으로 lis 의 "길이"가 정답
코드
import bisect
n = int(input())
arr = list(map(int, input().split()))
lis = []
for v in arr:
idx = bisect.bisect_left(lis, v)
if idx == len(lis):
lis.append(v)
else:
lis[idx] = v
print(len(lis))