Topological Sorting (위상 정렬)
DAG에서 최단경로를 찾기 위해서는 먼저 위상정렬을 수행하여 topological order를 찾아야 한다.
위상 정렬을 하는 방법은 아래 포스트에 정리해놓았다.
https://velog.io/@hyeon3356/DAG-%EC%97%90%EC%84%9C-Shortest-Path-%EC%B0%BE%EA%B8%B0
최단 거리 찾기
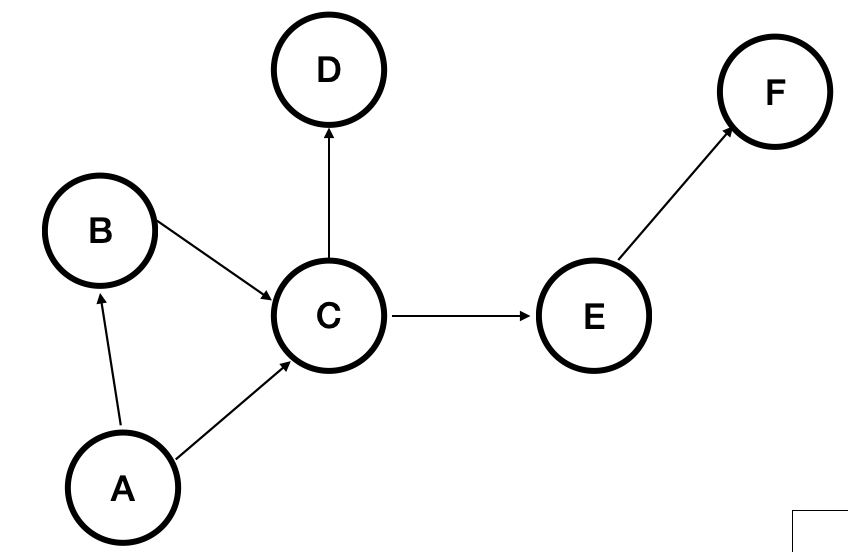
위와 같은 DAG 가 존재하고 모든 간선의 weight 는 1이라고 한다.
topological order 가 A -> B -> C -> D -> E -> F 라는 것을 이미 구했다고 하자.
시작점 A로부터 모든 정점들의 최단 경로를 구해보자.
step 0
먼저 최단 경로를 저장할 배열을 선언해야 한다. A는 시작점이므로 거리를 0으로 초기화하고 나머지 노드들은 모드 무한대로 초기화한다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
step 1
A 노드와 edge 로 연결된 B와 C의 경로를 업데이트 해주고, 큐에 넣는다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | 1 | 1 | ∞ | ∞ | ∞ |
step 2
큐에서 B 노드를 꺼내고 B와 간선이 연결된 C에 대해 거리를 확인한다.
기존 B의 최단 거리가 1이고 C와 연결된 간선의 weight도 1이므로 1+1=2 이다. 기존 C의 최단 거리가 1이므로 1 < 2이다. 따라서 C의 최단거리를 업데이트하지 않고 넘어간다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | 1 | 1 | ∞ | ∞ | ∞ |
step 3
큐에서 C 노드를 꺼내고 C와 연결된 D와 E를 차례로 큐에 넣고 거리를 업데이트 한다. C의 기존 거리가 1이므로 D와 E는 1+1=2와 ∞ 중 더 작은 값으로 업데이트 된다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | 1 | 1 | 2 | 2 | ∞ |
step 4
큐에서 D 노드를 꺼내고 간선을 확인한다. 연결된 간선이 없으므로 표는 업데이트 하지 않고 넘어간다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | 1 | 1 | 2 | 2 | ∞ |
step 4
큐에서 E 노드를 꺼내고 간선을 확인한다. F와 간선으로 연결되어 있으므로 F의 최단 거리를 업데이트한다.

| 노드 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 거리 | 0 | 1 | 1 | 2 | 2 | 3 |
최단 경로 찾기
최단 경로를 찾기 위해서는 최단 거리를 업데이트할 때, 어느 노드로부터의 간선으로 인해 거리가 업데이트 되었는지 노드의 정보도 함께 표에 저장해주면 된다. 그럼 노드의 정보를 거슬러 올라가며 출발점까지 알아낼 수 있다.
시간복잡도
DAG 그래프의 노드의 수를 V, 간선의 수를 E 라고 할 때,
- 위상정렬 : O(V + E)
- 최단거리 배열을 초기화 : O(V)
- 각 정점에 대해 간선을 확인하며 표를 업데이트 : O(E)
따라서 시간복잡도는 O(V + E) 이다.