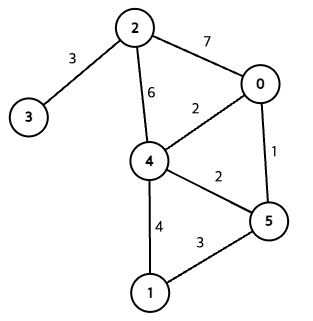
크루스칼 알고리즘

현재 간선들 중 가중치가 최소인 간선을 선택하는 그리디 알고리즘이다.
즉 최소 신장 트리(MST)를 만드는 대표적인 알고리즘이다.

1. 간선들을 가중치가 낮은 순서대로 오름차순 정렬한다.
2. 간선들을 확인해가며 싸이클이 형성되지 않는 간선들을 선택한다. (이 과정에서 Union Find 를 이용하여 싸이클 생성 여부를 파악한다.)

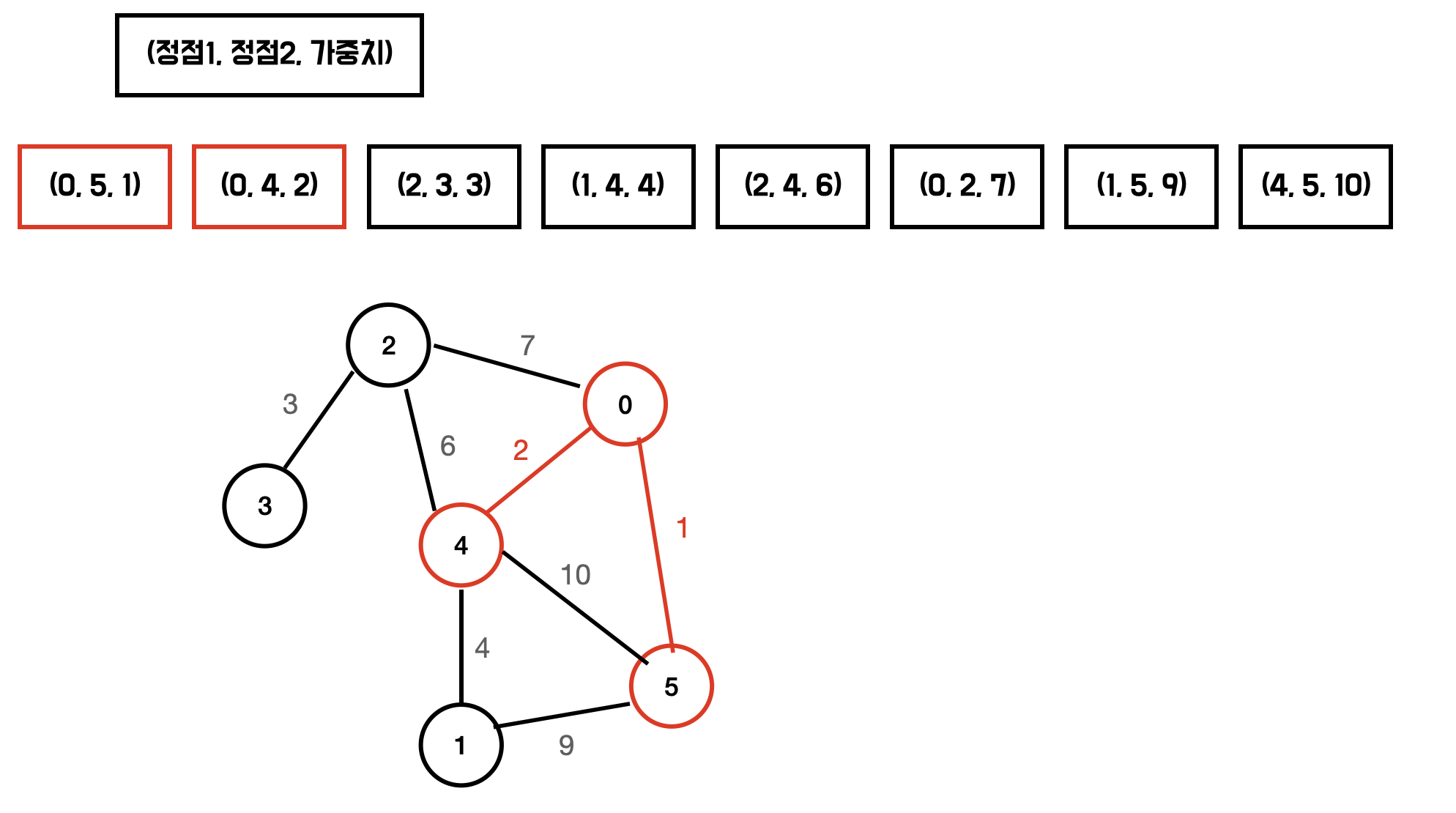
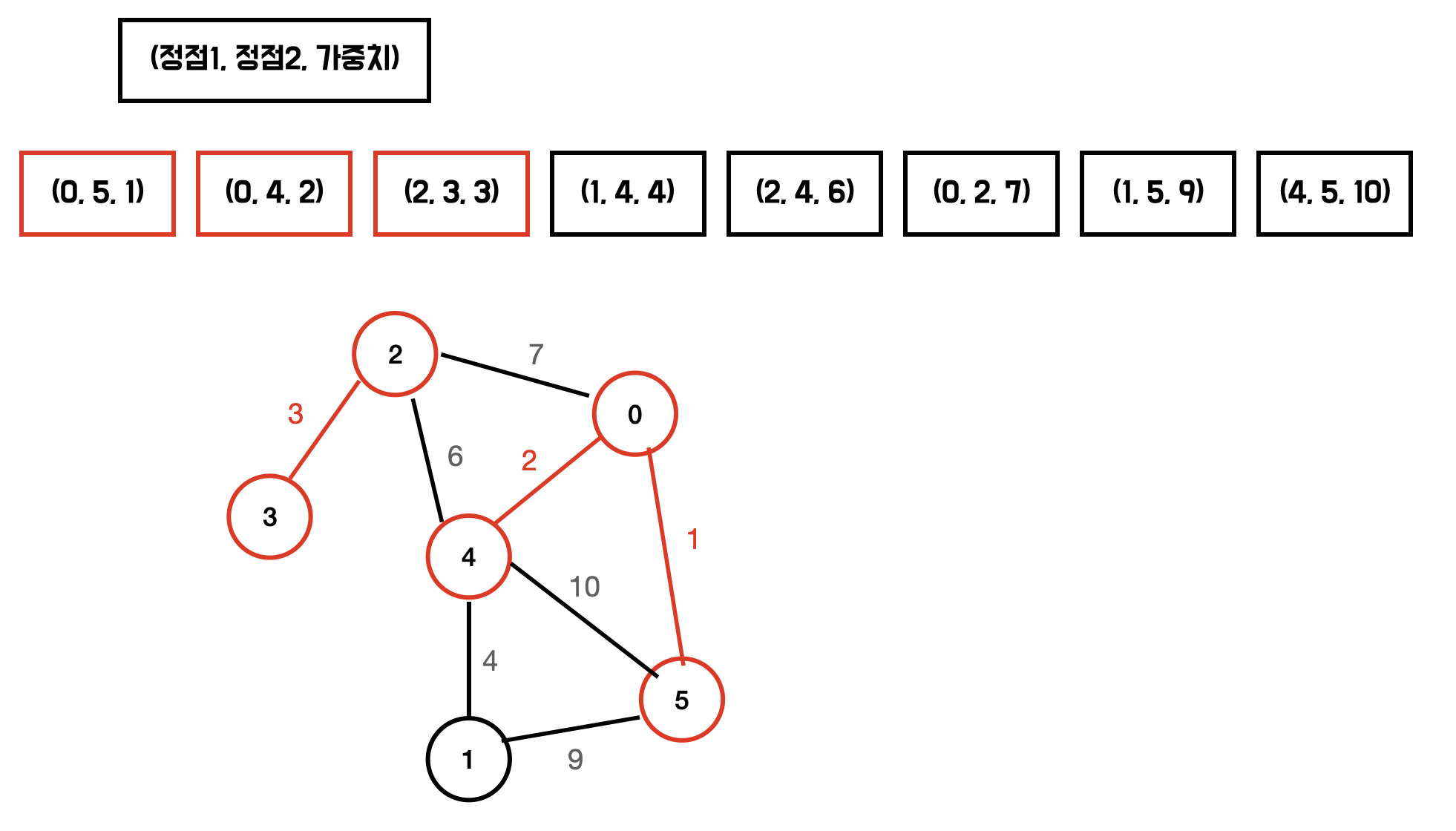
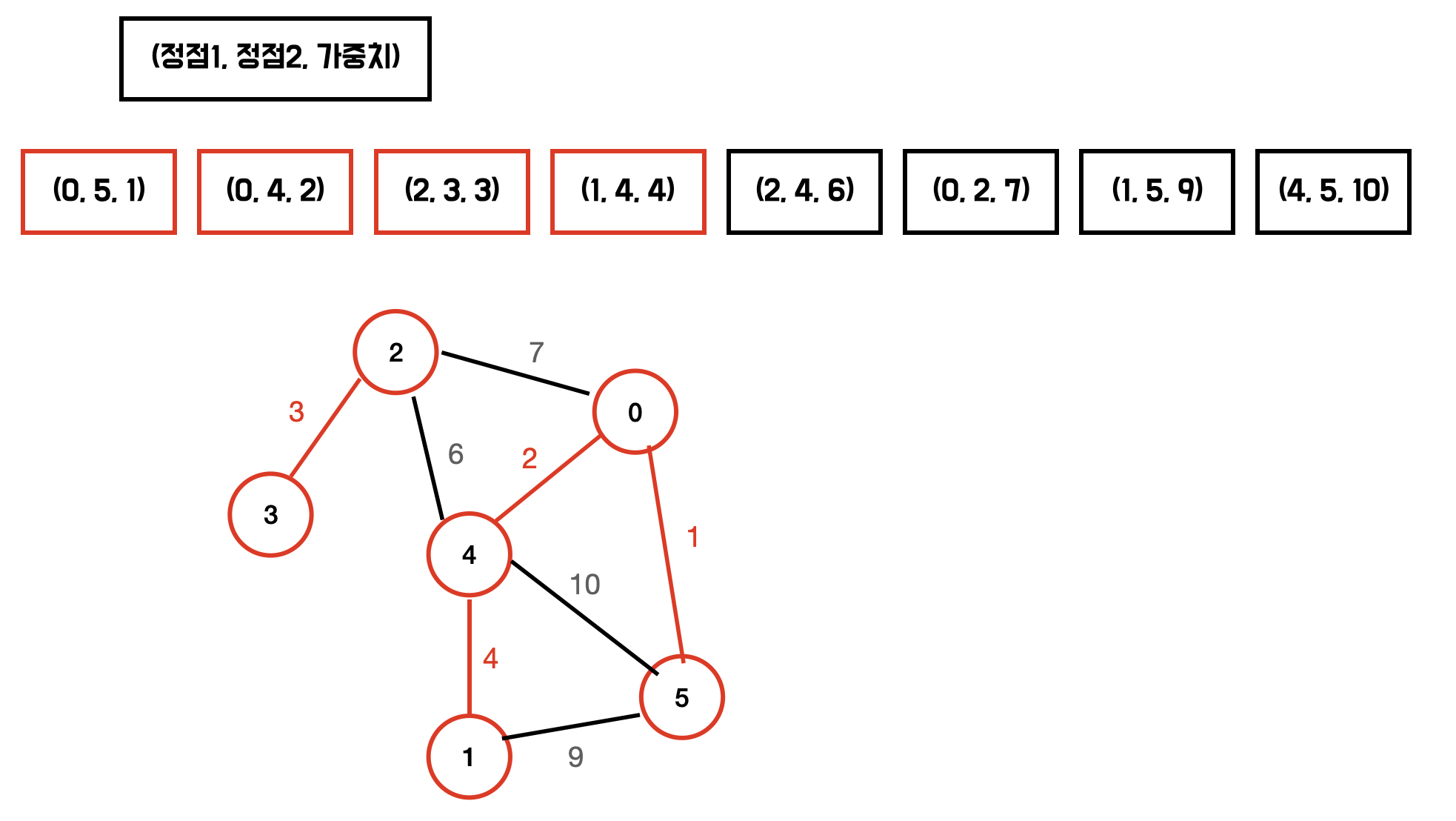
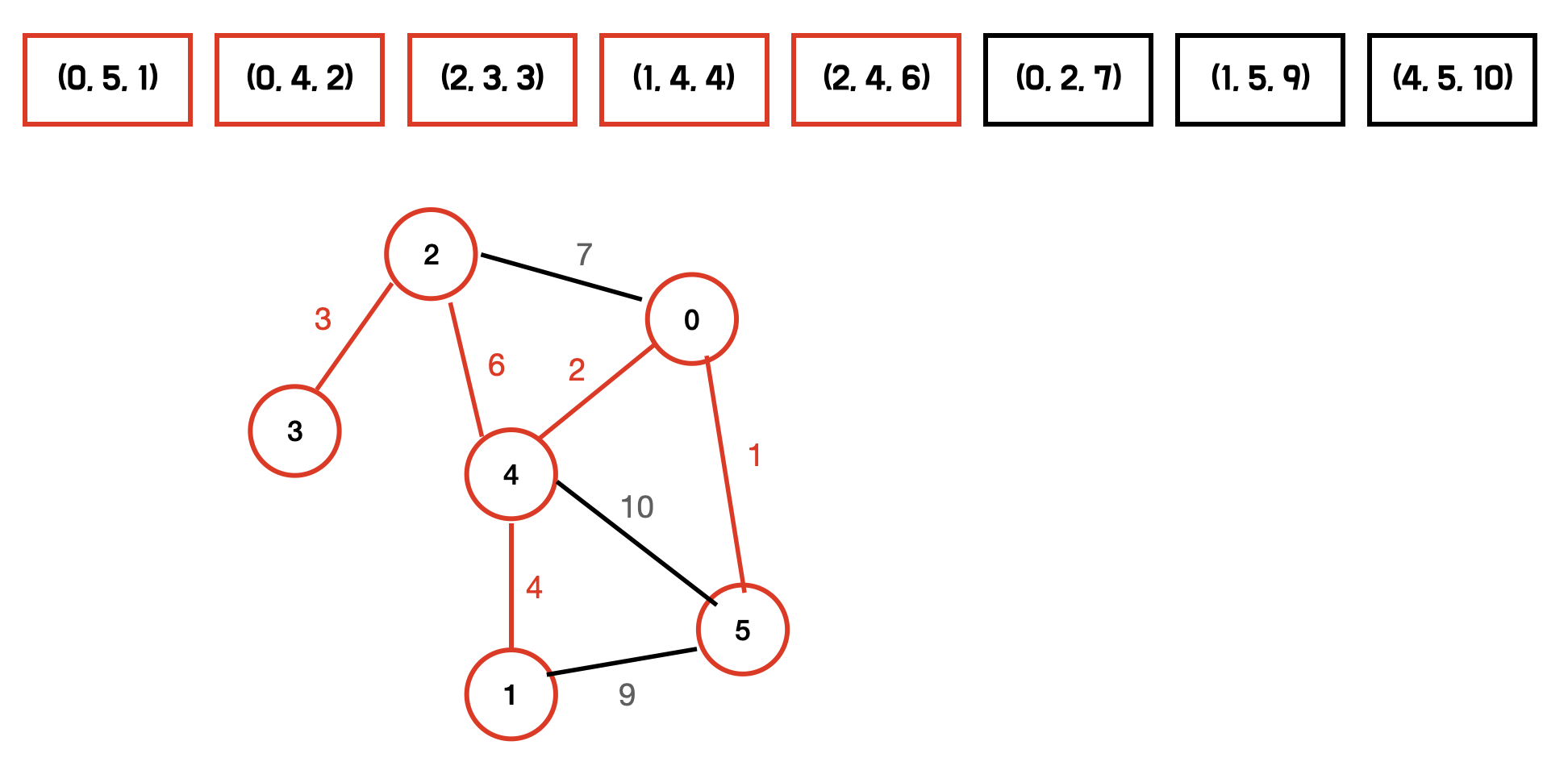
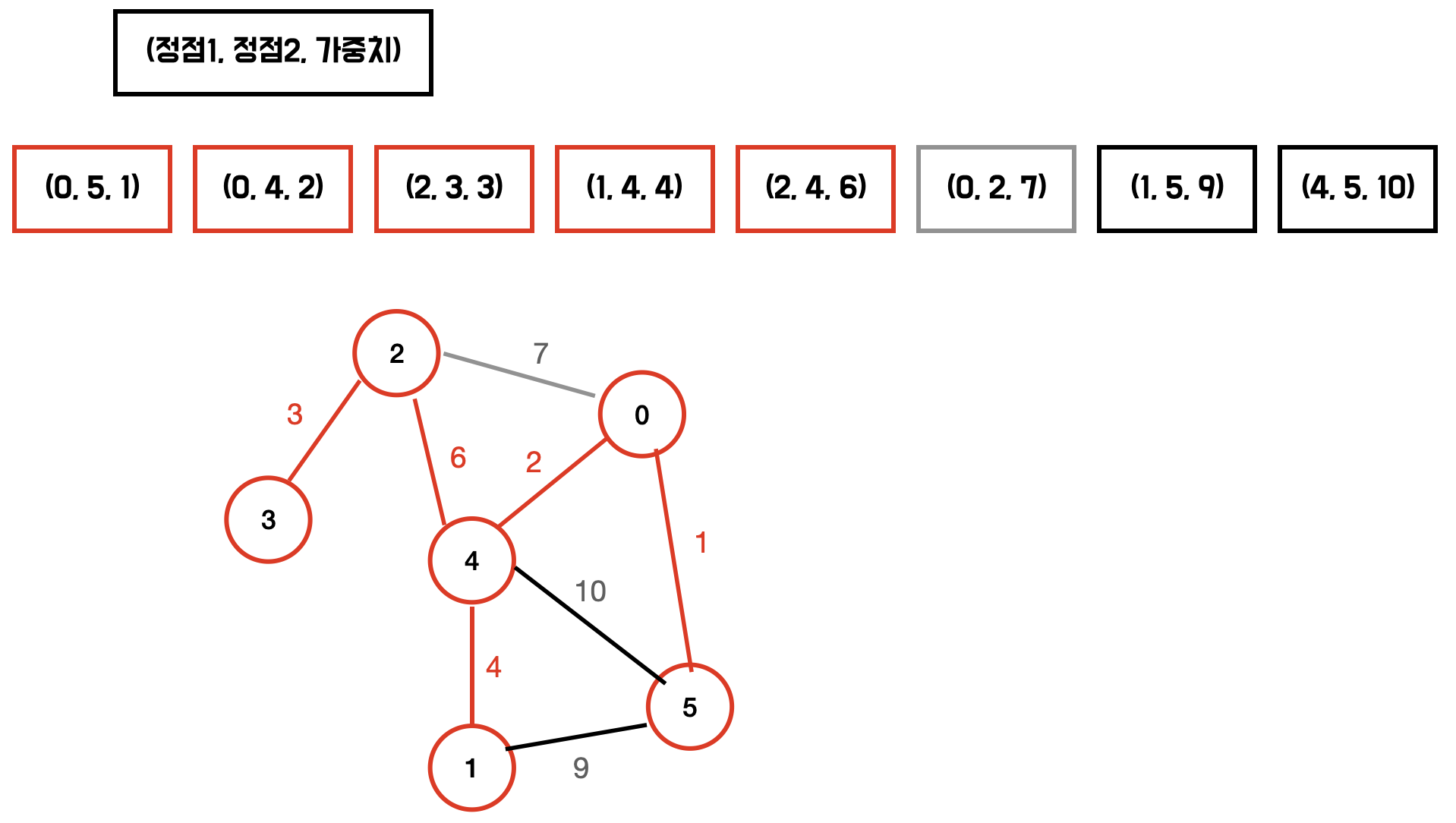
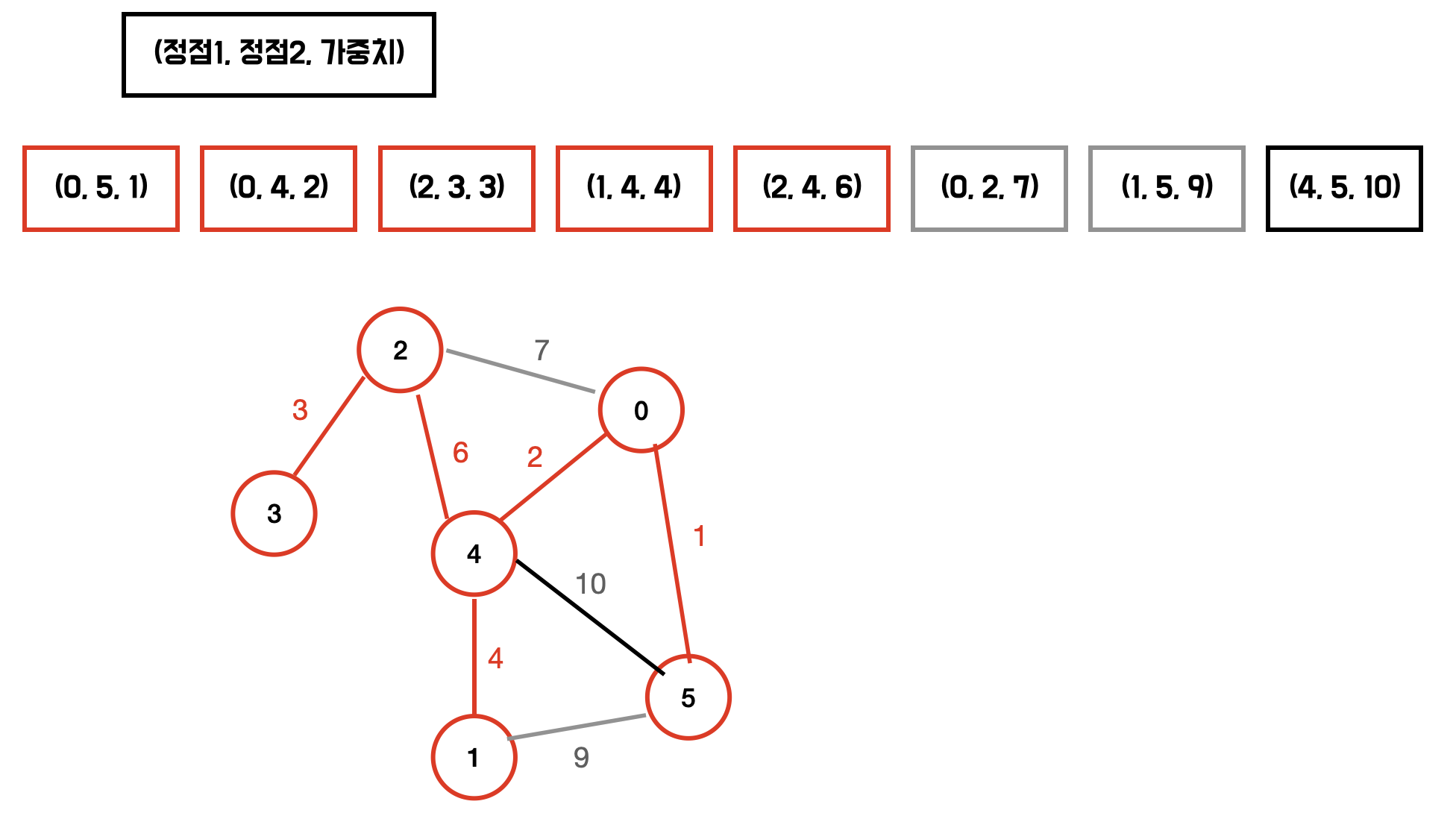
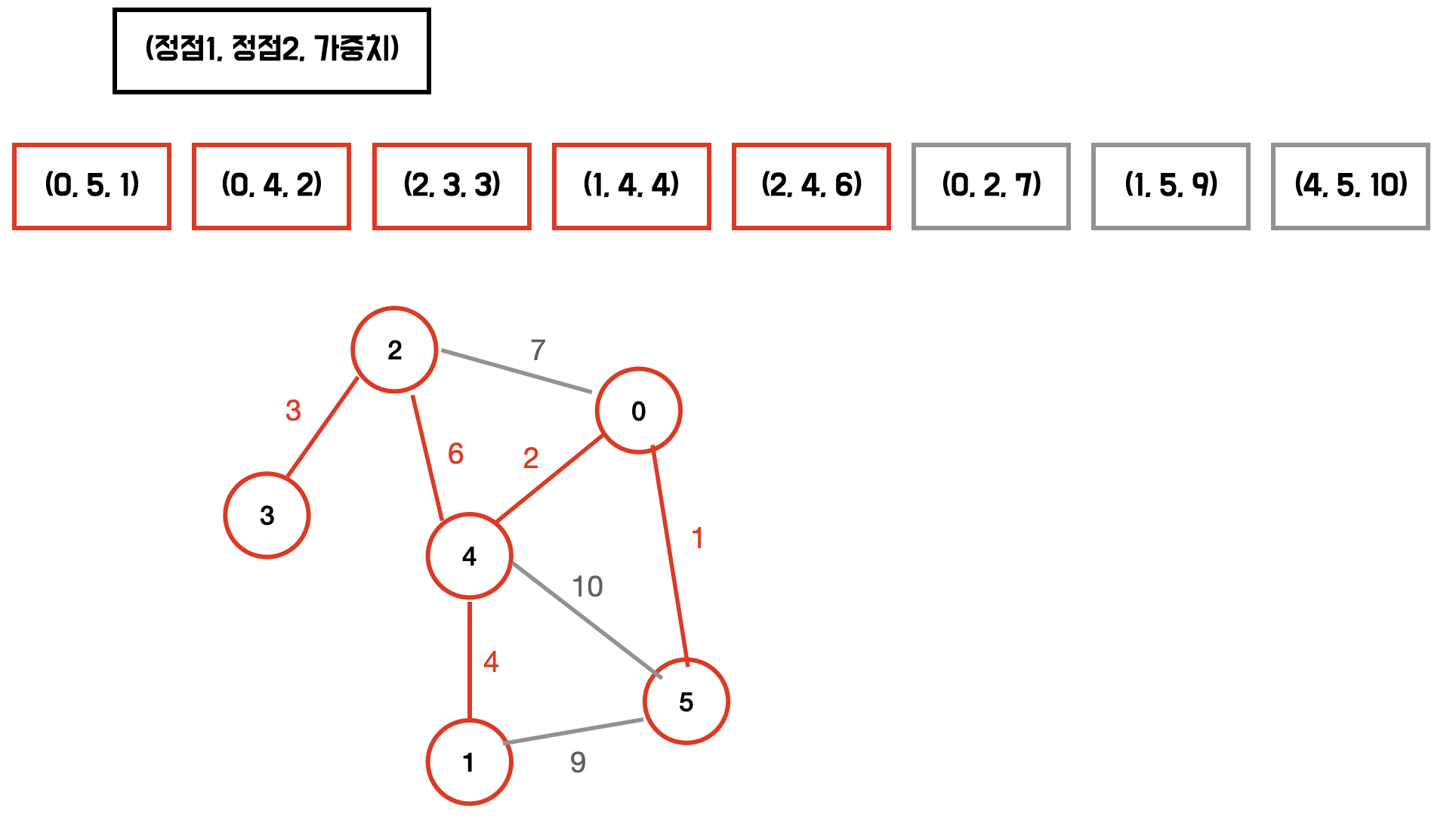
다음과 같은 그래프의 MSP를 구해보자.

union-find 를 이용하여 싸이클이 형성되는지 확인한다. 이미 같은 그룹에 속한다면 싸이클을 형성하는 것이다.

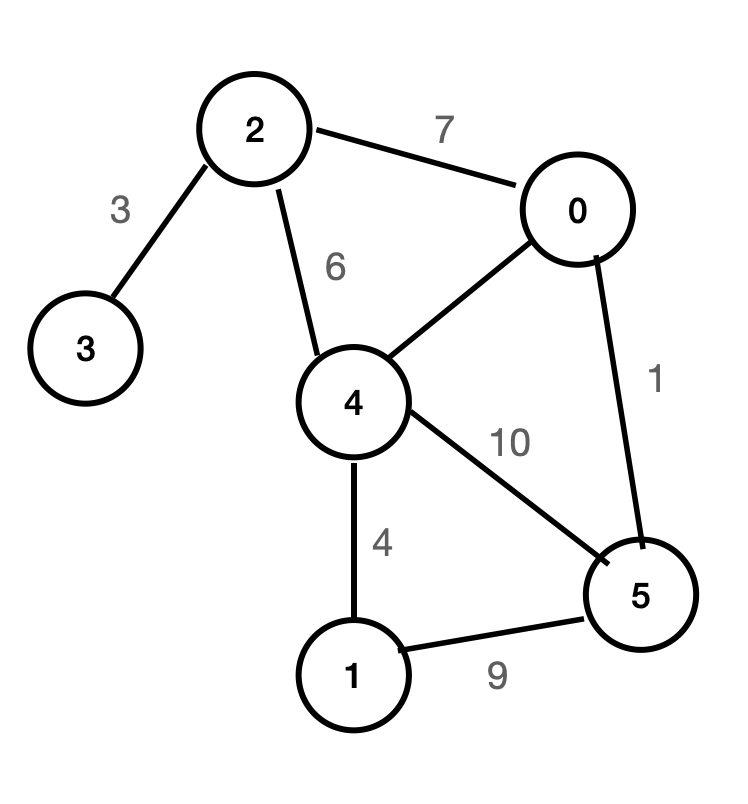
1. 모든 간선 정보를 가중치를 기준으로 오름차순 정렬시킨다.

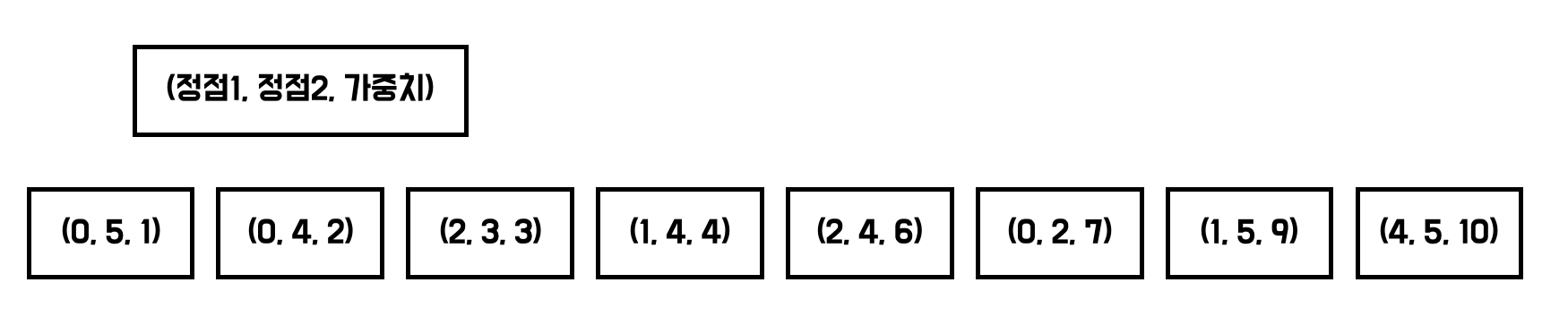
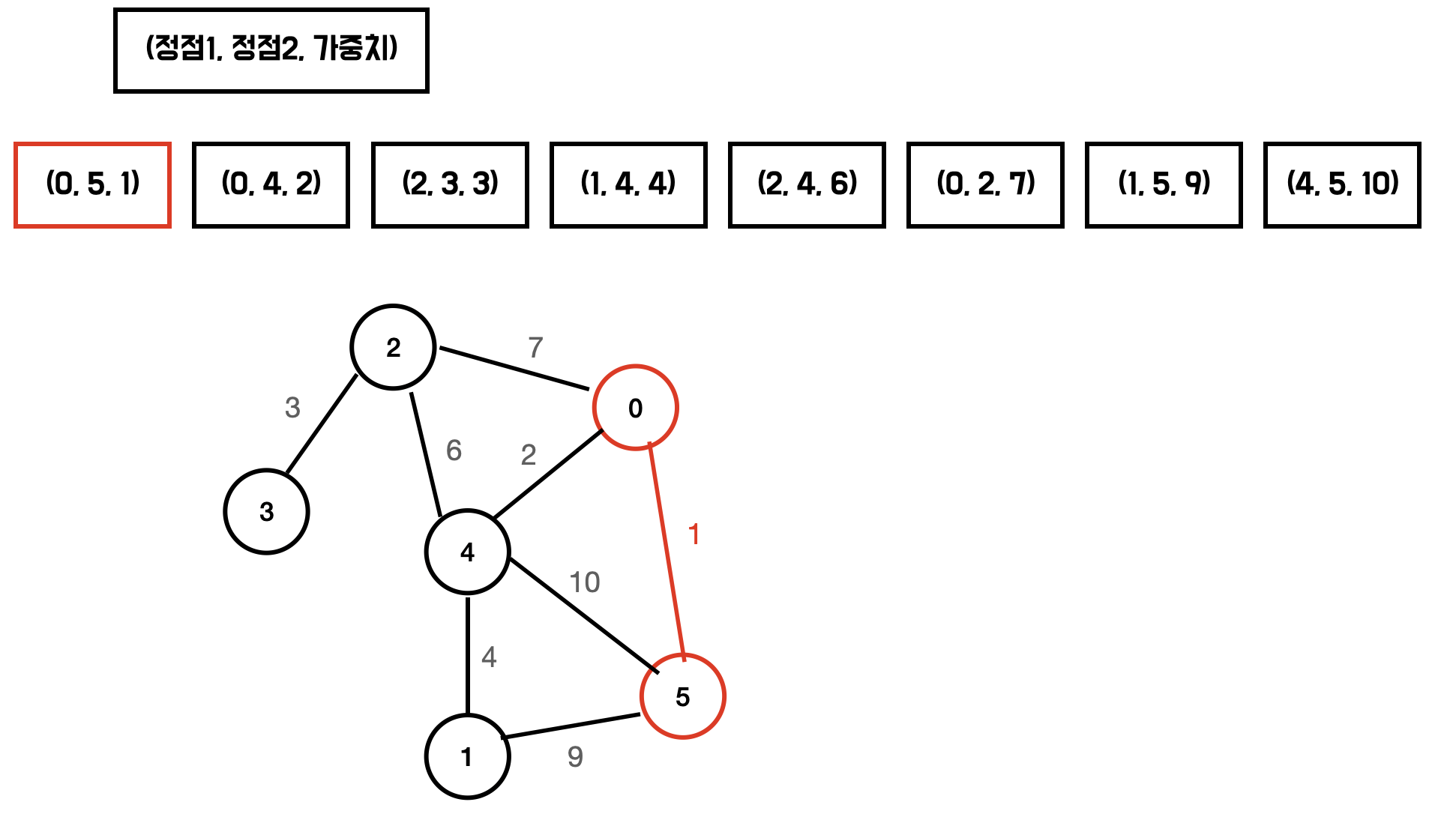
이제 가중치가 작은것부터 확인하며 다음의 과정을 반복하면 MST가 만들어진다.

2. 해당 간선을 포함시켰을 때 싸이클이 발생하는지 확인한다.
3. 싸이클이 형성되지 않는다면 해당 간선을 MST에 포함한다.

싸이클 형성 여부는 Union Find 를 사용하여 판단할 수 있다.

시간 복잡도

노드의 개수를 n, 간선의 개수를 m 이라고 하자.

각 간선을 정렬 : O(m log m)
각 간선에 대해 union-find 과정 : O(m log n)
따라서 최종 O(m log m + m log n) 이다.

예시 코드

코드트리 최소 스패닝 트리 = https://www.codetree.ai/missions/9/problems/minimum-spanning-tree/description

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

#define MX_N 10000

int uf[MX_N + 1];

class Edge{
public:
    int a;
    int b;
    int w;

    Edge(int a, int b, int w){
        this->a = a;
        this->b = b;
        this->w = w;
    }
};

int Find(int x){
    if(uf[x] == x) return x;
    return uf[x] = Find(uf[x]);
}

void Union(int a, int b){
    a = Find(a);
    b = Find(b);
    if(a != b){
        uf[a] = b;
    }
}

bool comp(Edge a, Edge b){
    if(a.w < b.w) return true;
    else return false;
}

int main() {
    int n, m;
    cin >> n >> m;

    for(int i = 1; i <= n; i++){
        uf[i] = i;
    }

    vector<Edge> edges;
    
    for(int i = 0; i < m; i++){
        int a, b, w;
        cin >> a >> b >> w;

        edges.push_back(Edge(a, b, w));
    }

    sort(edges.begin(), edges.end(), comp);

    ll ans = 0; // 선택한 가중치들의 합
    for(auto it = edges.begin(); it != edges.end(); it++){
        int a = it->a;
        int b = it->b;
        int w = it->w;

        if(Find(a) != Find(b)){
            Union(a, b);
            ans += w;
        }
    }
    cout << ans;

    return 0;
}

참고

• 이것이 취업을 위한 코딩테스트다 with 파이썬
• https://blog.naver.com/ndb796/221230994142