DAG

Directed Acyclic Graph 로, 방향이 있고 사이클이 없는 그래프를 말한다.
DAG 에서 최단 경로를 찾기 위해 Topological Sorting(위상 정렬)을 이용할 수 있다.

Topological Sorting

DAG 에서는 사이클이 없기 때문에 Topological Order를 정의할 수 있다. 그리고 이 Topological Order를 찾아내는 과정을 Topological Sorting 이라고 한다. (Topological Order는 유일하지 않을 수 있다.)

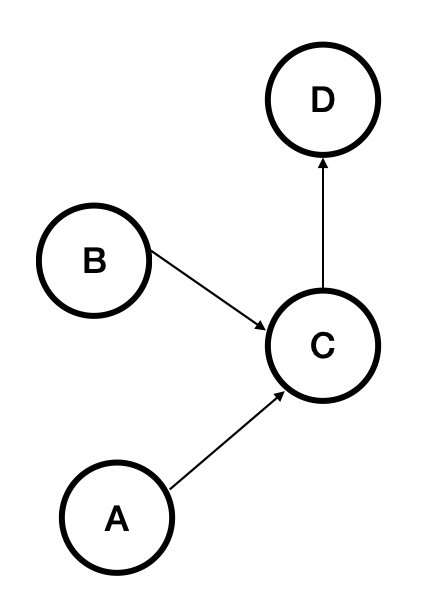
위와 같은 DAG 가 있다고 생각했을 때, Topological Order는 두 가지로 찾을 수 있다.
1. A -> B -> C -> D
2. B -> A -> C -> D

indegree 와 outdegree

먼저 topological sorting 을 이해하기 위해 indegree와 outdegree 가 무엇인지 알아야 한다.

• indegree : 특정한 노드로 들어오는 간선의 개수
• outdegree : 특정한 노드에서 나가는 간선의 개수

-	A	B	C	D
indegree	0	0	2	1
outdegree	1	1	1	0

topological sorting 과정

접근방법은 2가지로, incoming edge가 없는 정점부터 탐색하는 방법과 outgoing edge가 없는 정점부터 탐색하는 방법이 있다.

여기서는 incoming edge가 없는 정점부터 탐색하는 방법을 알아보자.

step 0

indegree가 0인 모든 노드를 큐에 넣는다. 현재 노드 A 만 indegree 가 0 이므로 A 를 큐에 넣는다.

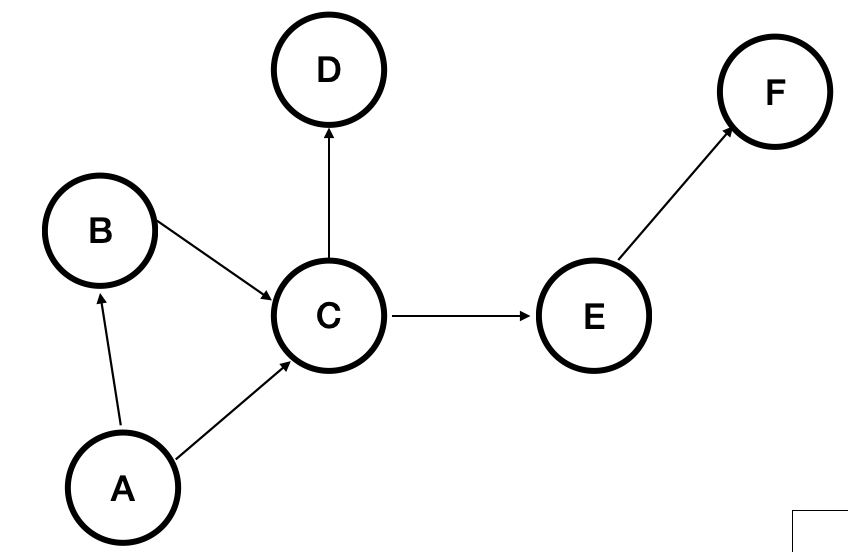
노드	A	B	C	D	E	F
indegree	0	1	2	1	1	1

큐	1	2	3	4	5	6
큐	A

step 1

큐에 있는 A 노드를 꺼내고 outgoing edge 들을 제거한다. 그러면 B의 indegree 가 0이 되므로 B 를 큐에 넣는다.

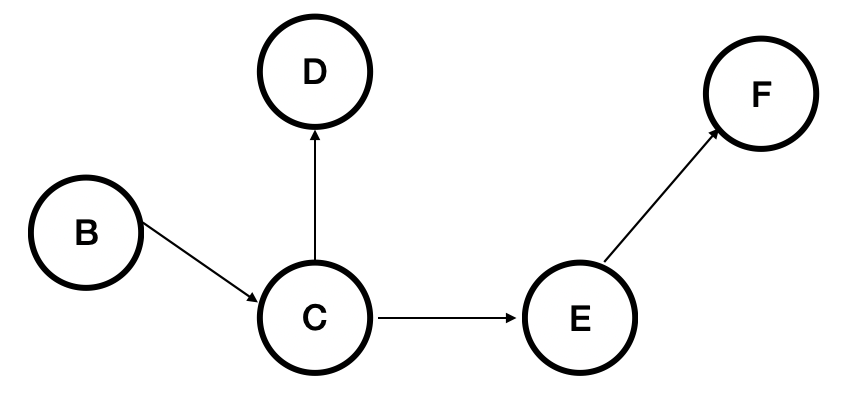
노드	A	B	C	D	E	F
indegree	0	0	1	1	1	1

큐	1	2	3	4	5	6
큐	B

step 2

큐에 있는 B 노드를 꺼내고 outgoing edge를 제거하면 C의 indegree 가 0이 된다. 따라서 C를 큐에 넣는다.

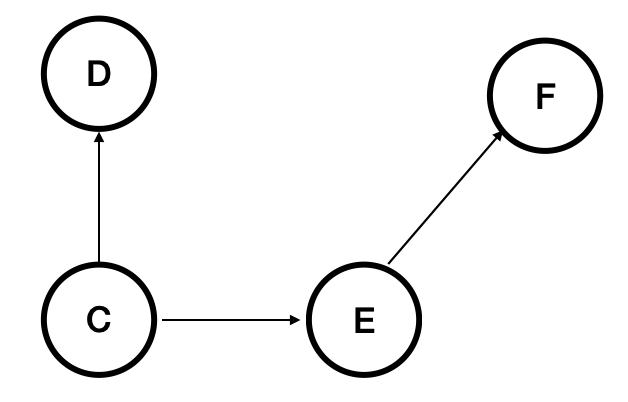
노드	A	B	C	D	E	F
indegree	0	0	0	1	1	1

큐	1	2	3	4	5	6
큐	C

step 3

큐에 있는 C 노드를 꺼내고 outgoing edge를 제거하면 D, E의 indegree 가 0이 된다. 따라서 D, E를 큐에 넣는다.

노드	A	B	C	D	E	F
indegree	0	0	0	0	0	1

큐	1	2	3	4	5	6
큐	D	E

step 4

큐에 있는 D 노드를 꺼낸다. D에는 outgoing edge가 없으므로 indegree 표는 업데이트 하지 않는다.

노드	A	B	C	D	E	F
indegree	0	0	0	0	0	1

큐	1	2	3	4	5	6
큐	E

step 5

큐에 있는 E 노드를 꺼낸다. E의 outgoing edge를 없애면 F 의 indegree가 0이 되므로 표를 업데이트하고, 큐에 넣는다.

노드	A	B	C	D	E	F
indegree	0	0	0	0	0	0

큐	1	2	3	4	5	6
큐	F

결과

A -> B -> C -> D -> E -> F

topological sorting 특징

• DAG 에서만 수행할 수 있다.
• topological order 가 유일하지 않을 수 있다.
• 모든 노드를 방문하기 이전에 큐가 빈다면, 사이클이 존재하는 것이다.
• 보통 큐로 구현하지만, 스택을 이용한 DFS 로도 구현할 수 있다.

시간 복잡도

노드의 개수를 V, edge의 개수를 E라고 하면, 위상 정렬의 시간복잡도는 O(V + E)이다.

문제

https://www.acmicpc.net/problem/2252

코드

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

#define MX_N 32000

// 학생 그래프
vector<int> student[MX_N+1];

int indegree[MX_N+1];
int isused[MX_N + 1];

int main(){
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    // 학생수
    int n;
    cin >> n;

    // 키 비교 횟수
    int m;
    cin >> m;

    int a, b;
    for(int i = 0; i< m; i++){
        cin >> a >> b;
        student[a].push_back(b);

        indegree[b]++;
    }

    // 학생들을 줄을 세운 결과를 차례대로 넣을 벡터
    vector<int> ans;
    
    // 학생들의 번호를 넣을 큐
    queue<int> Q;

    // indegree 가 0인 거 큐에 넣기
    for(int i = 1; i <= n; i++){
        if(indegree[i] == 0) {
            isused[i] = 1;
            Q.push(i);
        }
    }

    while(!Q.empty()){
        int num = Q.front(); Q.pop();
        ans.push_back(num);
        /**
         * num 번 학생과 연결된 outgoing edge를 따라가서 
         * 그 학생들의 indegree를 1씩 감소
        */
        for(auto it = student[num].begin(); it != student[num].end(); it++){
            indegree[*it]--;

            // indegree 가 0이 되었으면 큐에 넣기
            if(indegree[*it] == 0 && !isused[*it]) {
                isused[*it] = 1;
                Q.push(*it);
            }
        }
    }

    for(auto it = ans.begin(); it != ans.end(); it++){
        cout << *it << " ";
    }
}

출처

• https://velog.io/@kimdukbae/%EC%9C%84%EC%83%81-%EC%A0%95%EB%A0%AC-Topological-Sorting