
💻 프로젝트 소개
- 다이아몬드 데이터 EDA에 사용했었던 kaggle의 데이터셋을 이용하여 가격과 상관계수가 높은 요소를 채택하여 단순선형회귀를 통해 가격을 예측해보았다.
📁 데이터셋
[데이터셋 구성]
- price: 가격
- carat: 무게
- cut: 커팃의 퀄리티
- color: 색
- clarity: 투명도
- x: 길이
- y: 너비
- z: 깊이
- table: 다이아몬드 상단의 너비
[파생변수]
- 파생변수로 부피, 표면적, 지름, 밀도를 만들었다.
- 부피:
x * y * z - 표면적:
2*(x*y+y*z+z*x) - 지름:
(x+y+z)/3 - 밀도:
carat/volume
- 부피:
[Bofore]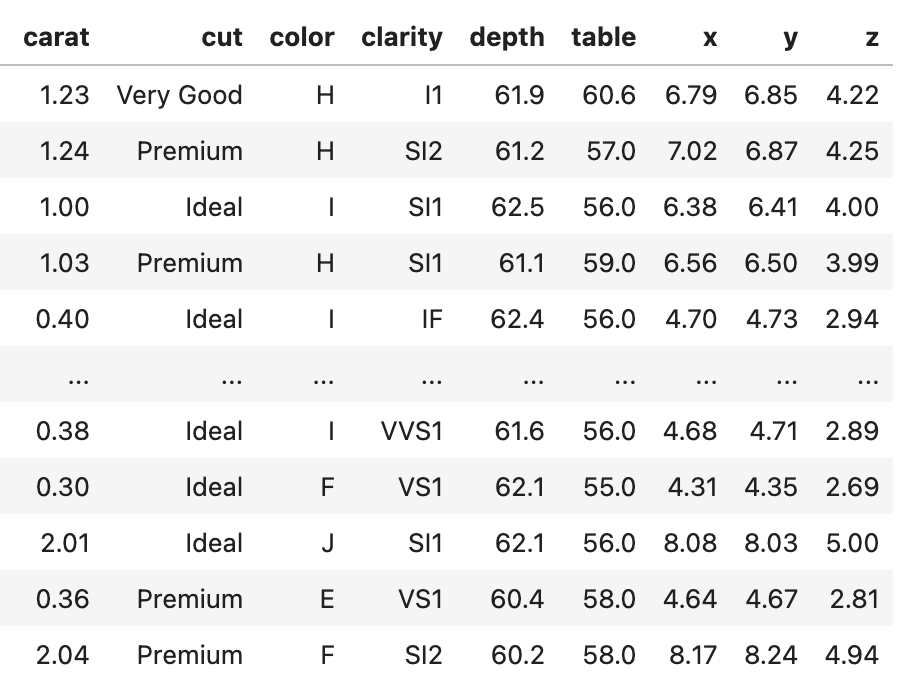 | [After]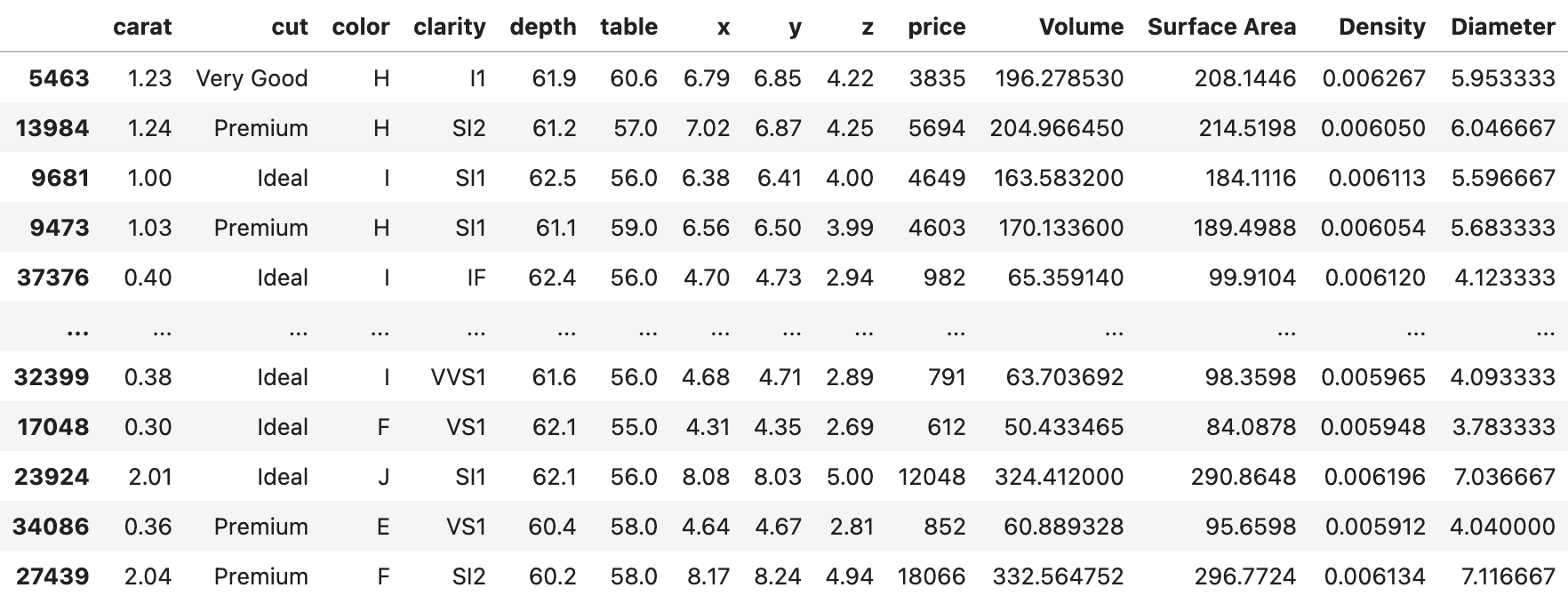 |
|---|
- price와의 상관관계를 살펴보니 carat, 표면적, 부피 순으로 가격과 상관관계가 높게 나왔다. 따라서 3개의 항목을 사용하여 단순회귀모형을 만들어보려고 한다.
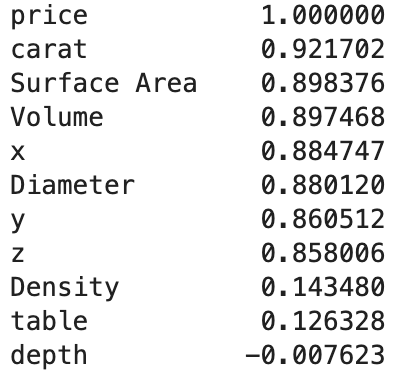
📈 단순선형회귀
[carat]
-
[price 로그 처리 X]
-
모델로 학습시켜준 후 price와 carat의 산점도 그래프를 그렸을때 아래와 같이 나타났다.
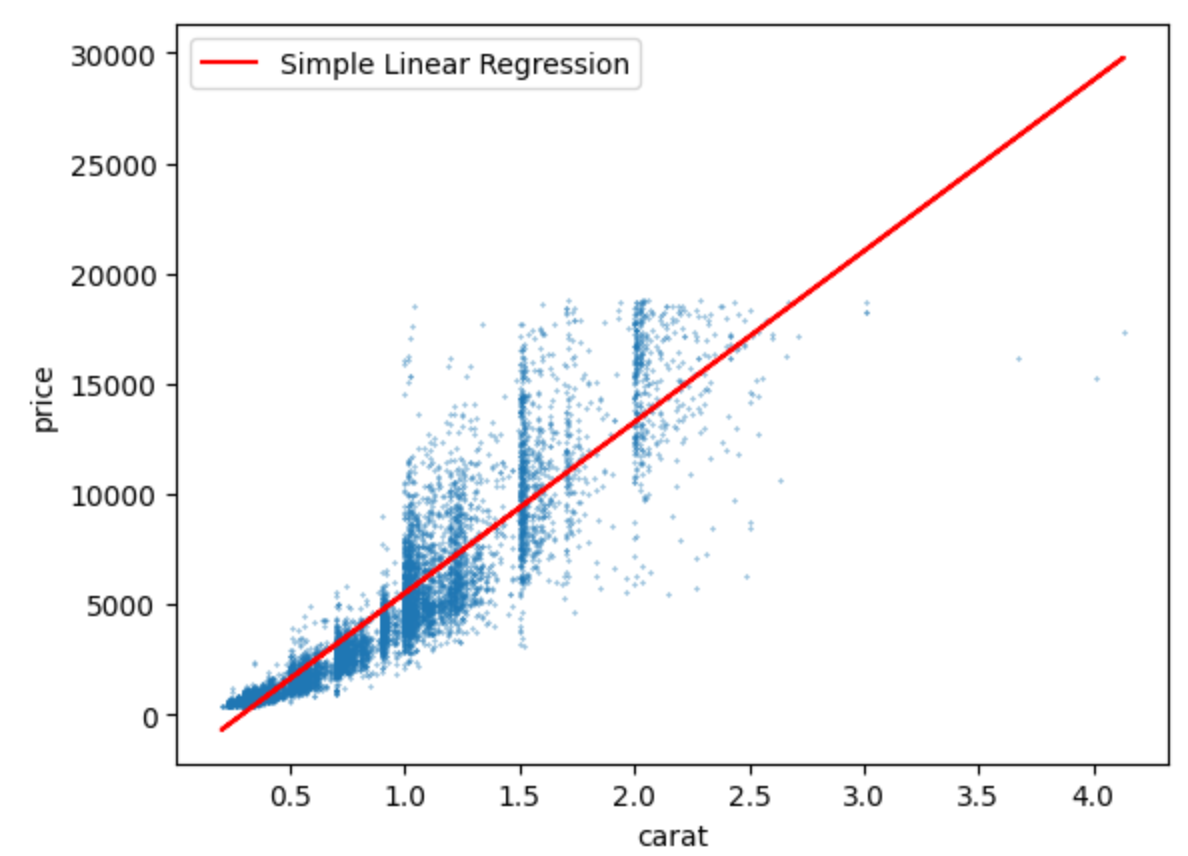
-
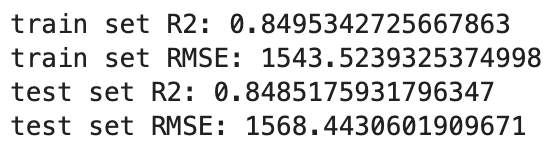
train set과 test set의 R square과 RMSE를 비교해보았을때, 두 세트 모두 R square가 약 0.85로 높은 정확도를 보이고 있었다.
-
-
[price 로그 처리 O]
- price의 그래프를 그려보았을때, 오른쪽 꼬리가 긴 형태가 나타났기 때문에 로그를 취해 정규분포 형태로 변환해주었다.
[Before] 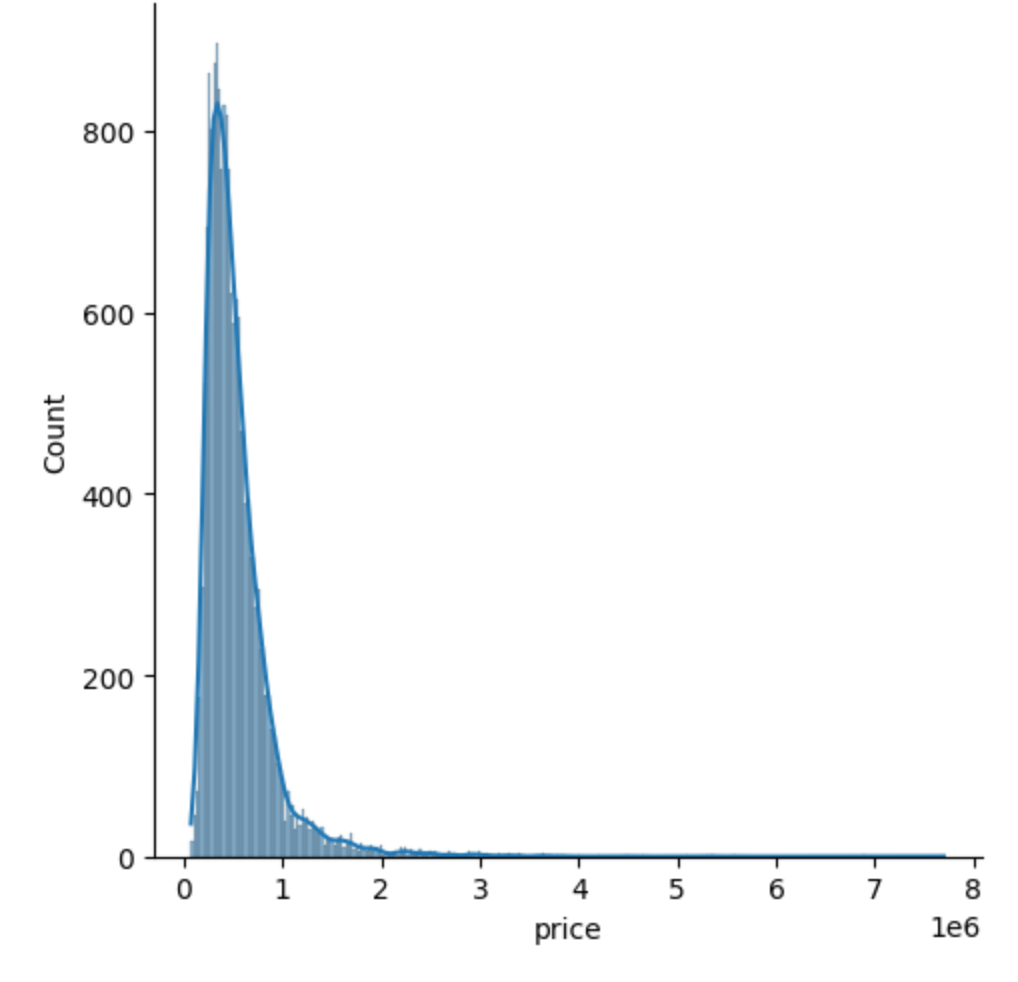
[After] 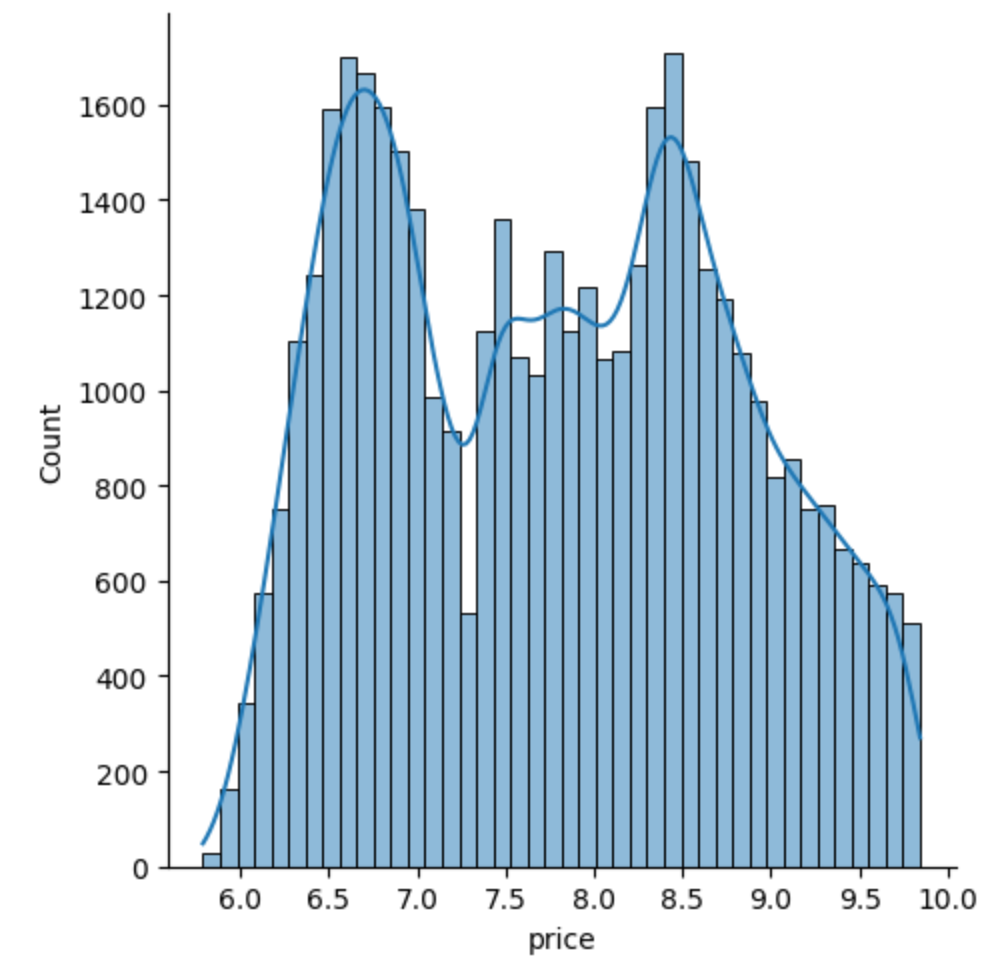
-
단순 선형 회귀로 학습시킨 후 산점도 그래프를 그려보니 가격에 로그를 취해주기 전보다 데이터들이 모여있었다.
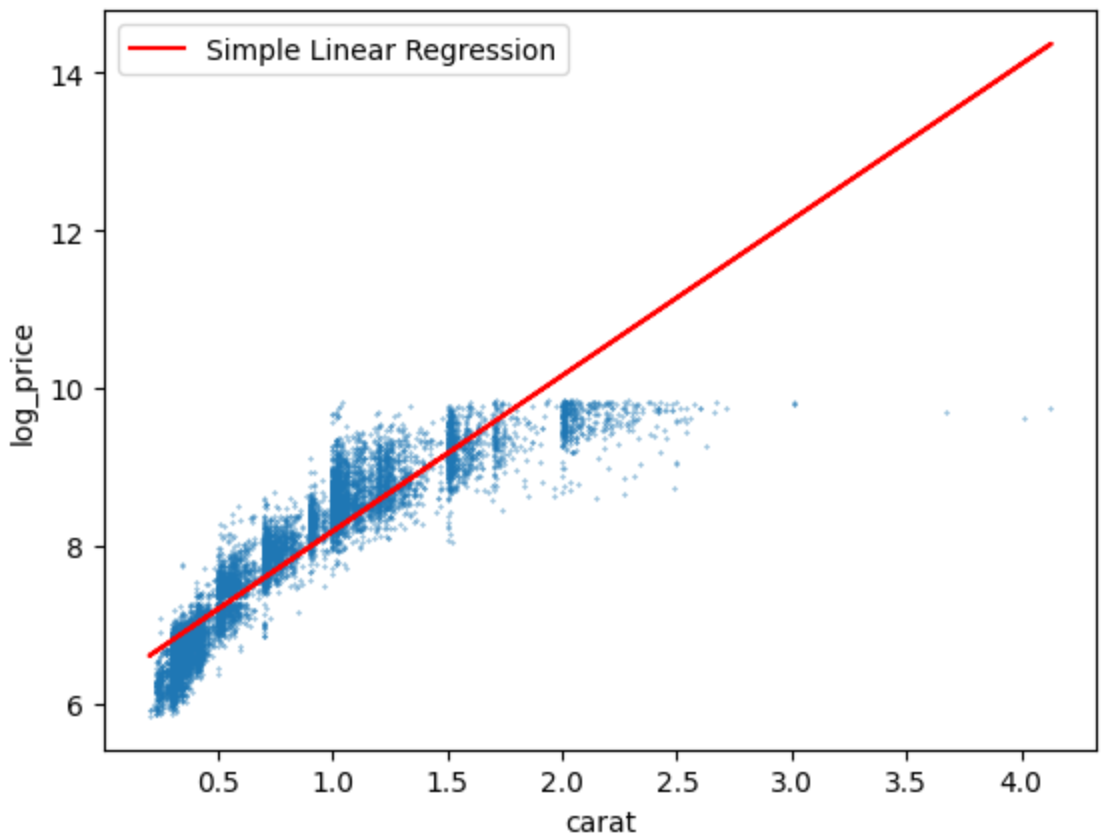
-
그러나 R square값을 비교해보면 오히려 로그를 취해준 후 아주 약간이지만 값이 낮아진 것을 확인할 수 있었다.

[표면적]
- 가격과 표면적의 산점도 그래프를 그려보니 carat과 비슷한 모양으로 데이터가 흩어져있었다.
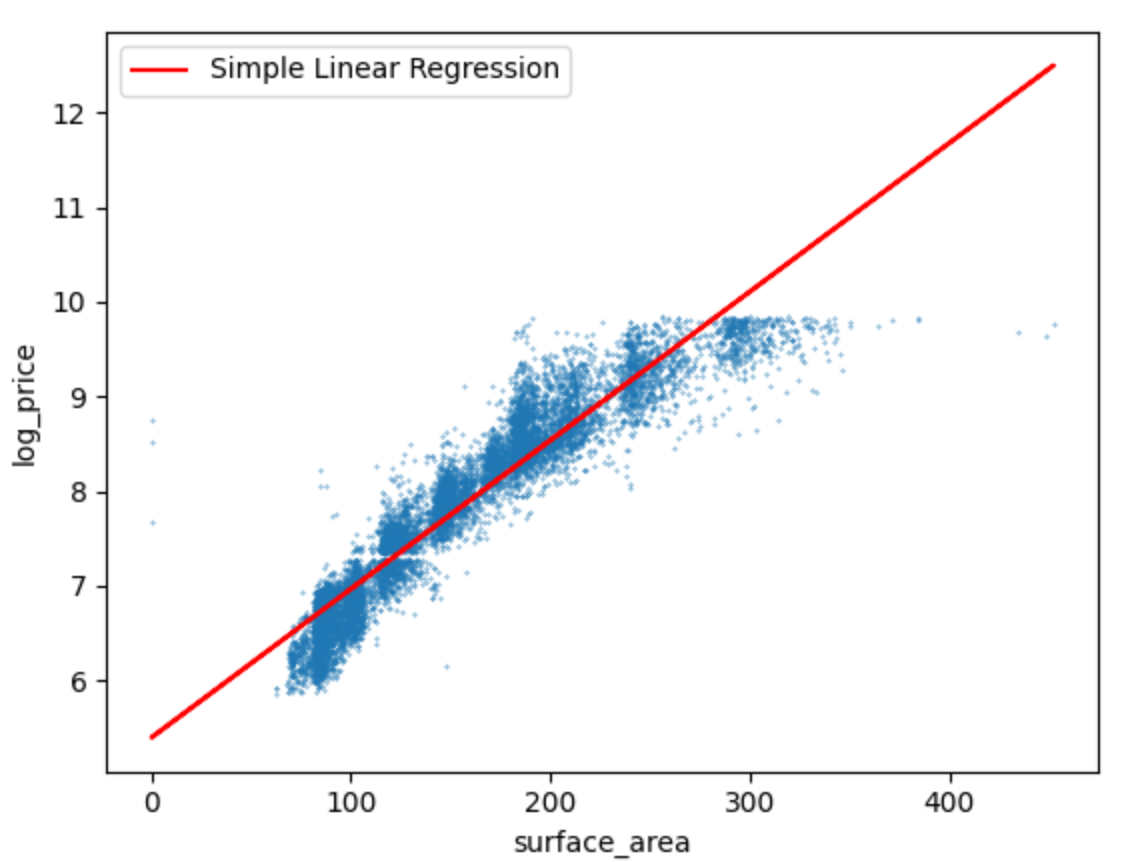
- 예상과는 달리 carat에 비해 예측정확도가 높았고, test set의 정확도가 train set 보다 높게 나왔다.

[부피]
- 가격과 부피의 산점도 그래프를 그려보니 carat과 비슷한 모양으로 데이터가 흩어져있었다.
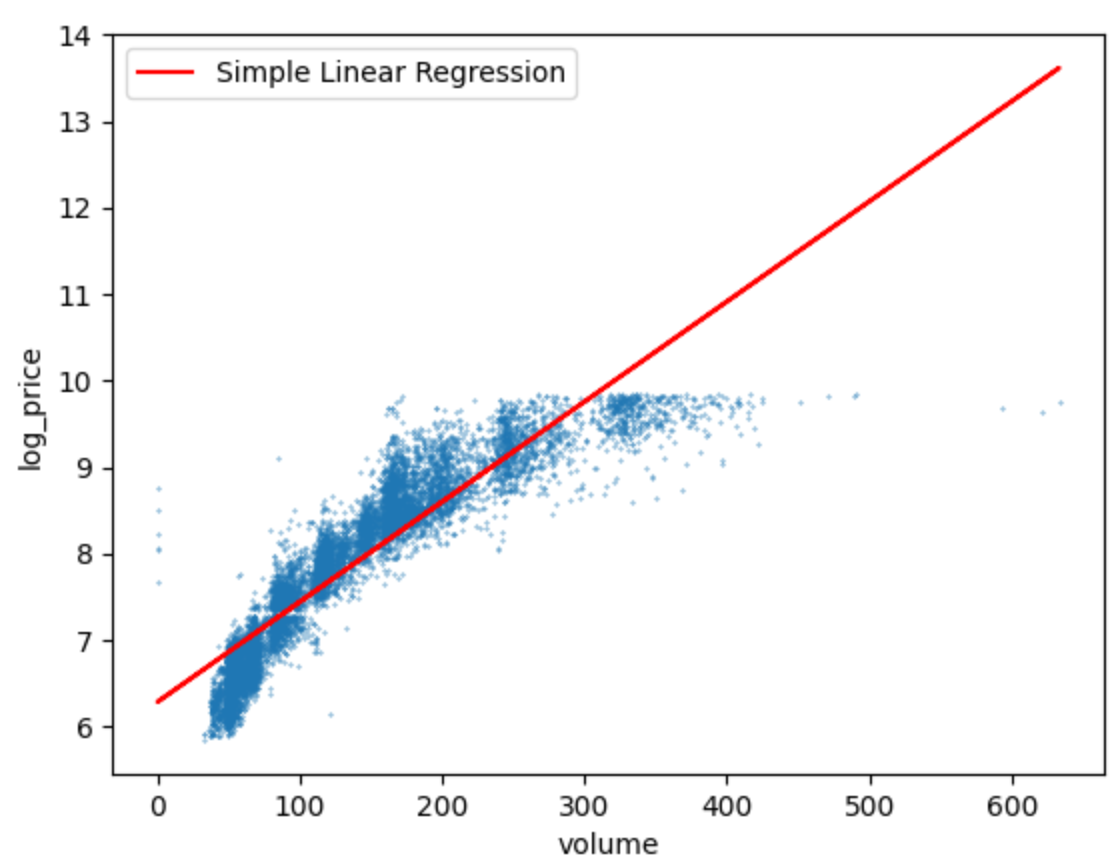
- 모델의 학습시킨 결과 train set의 정확도는 앞선 두 항목의 선형회귀 정확도보다 낮았고, test set의 정확도가 train set의 정확도보다 높았다.

💡 Insight
[Carat]
- carat
 |  |
|---|
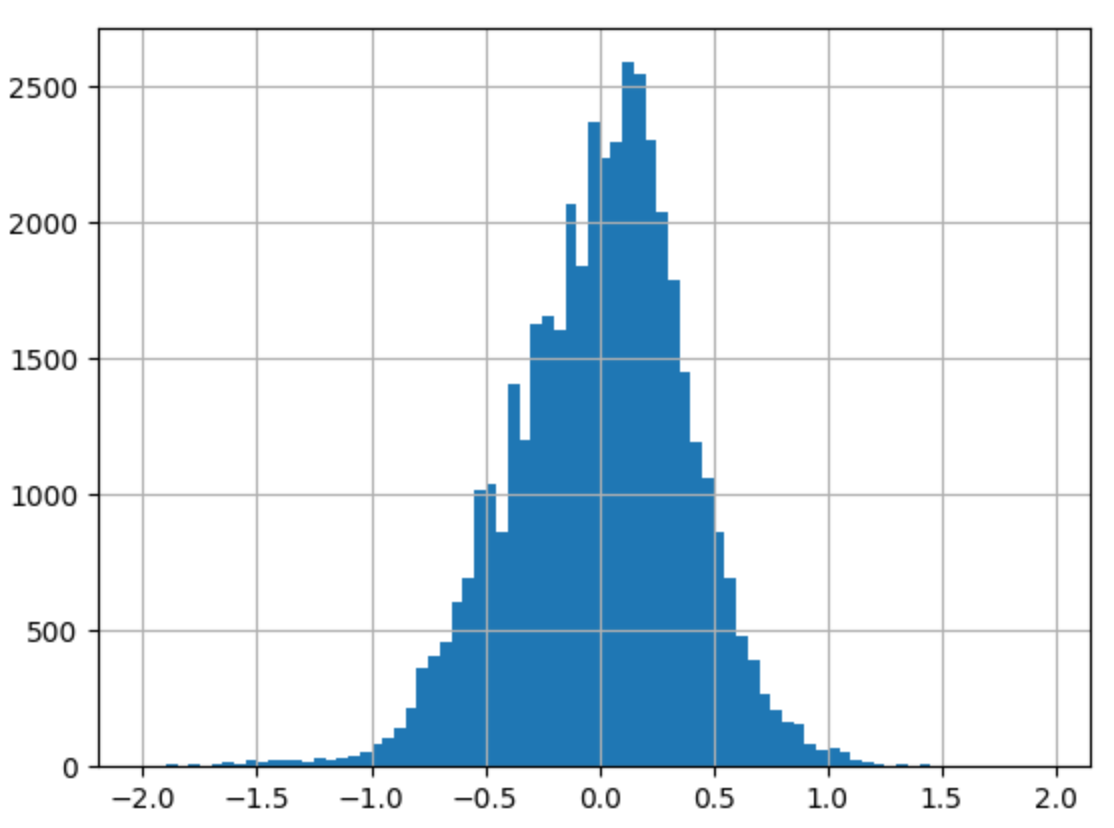
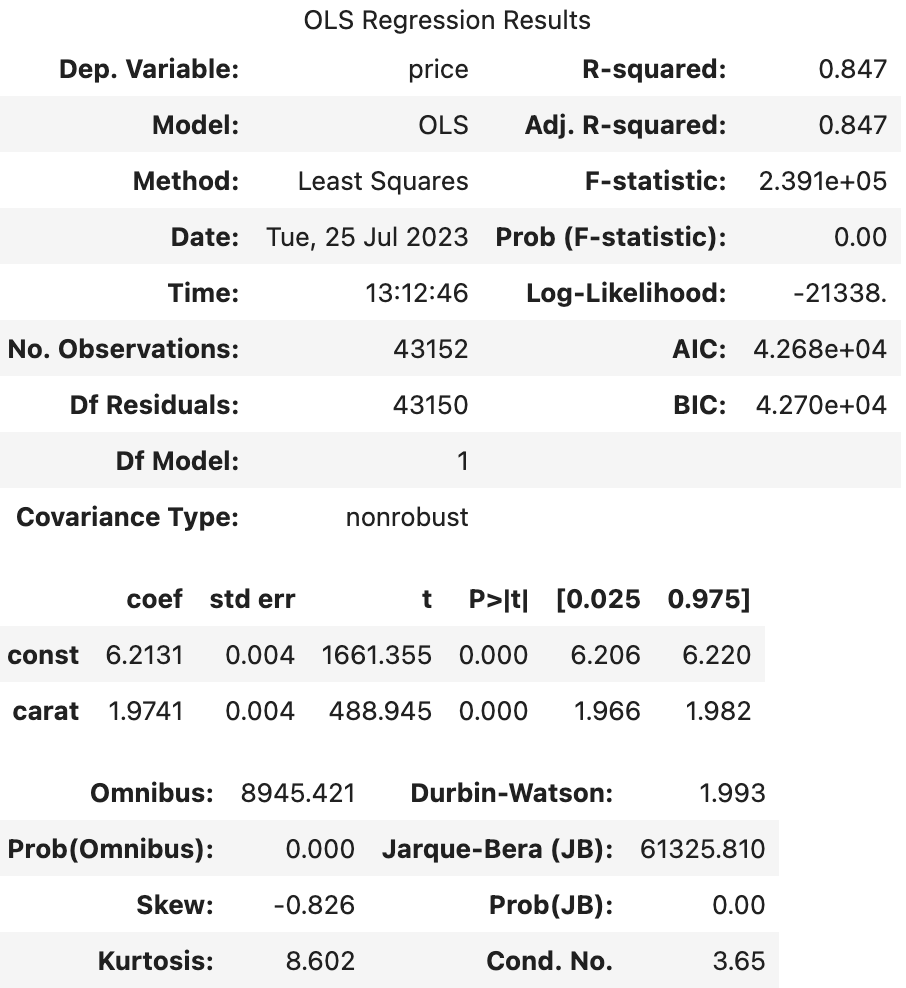
- price-> log / carat
 |  |
|---|
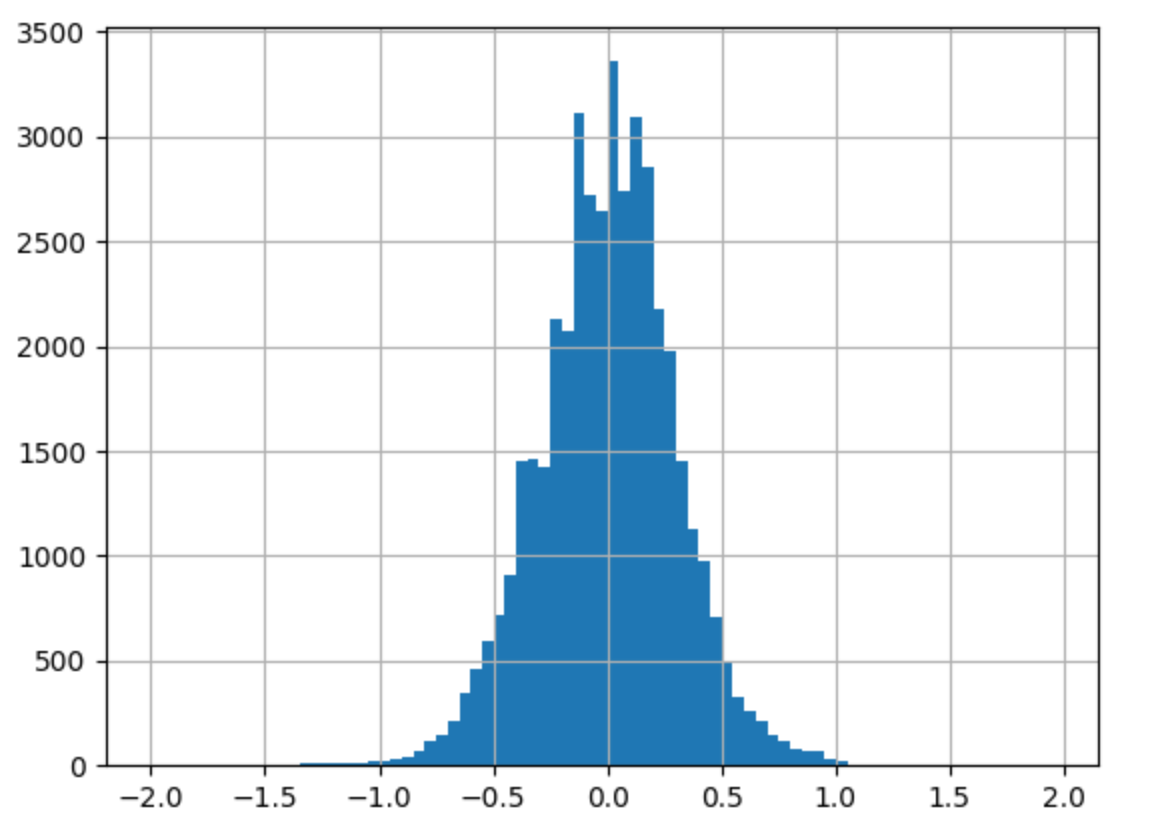
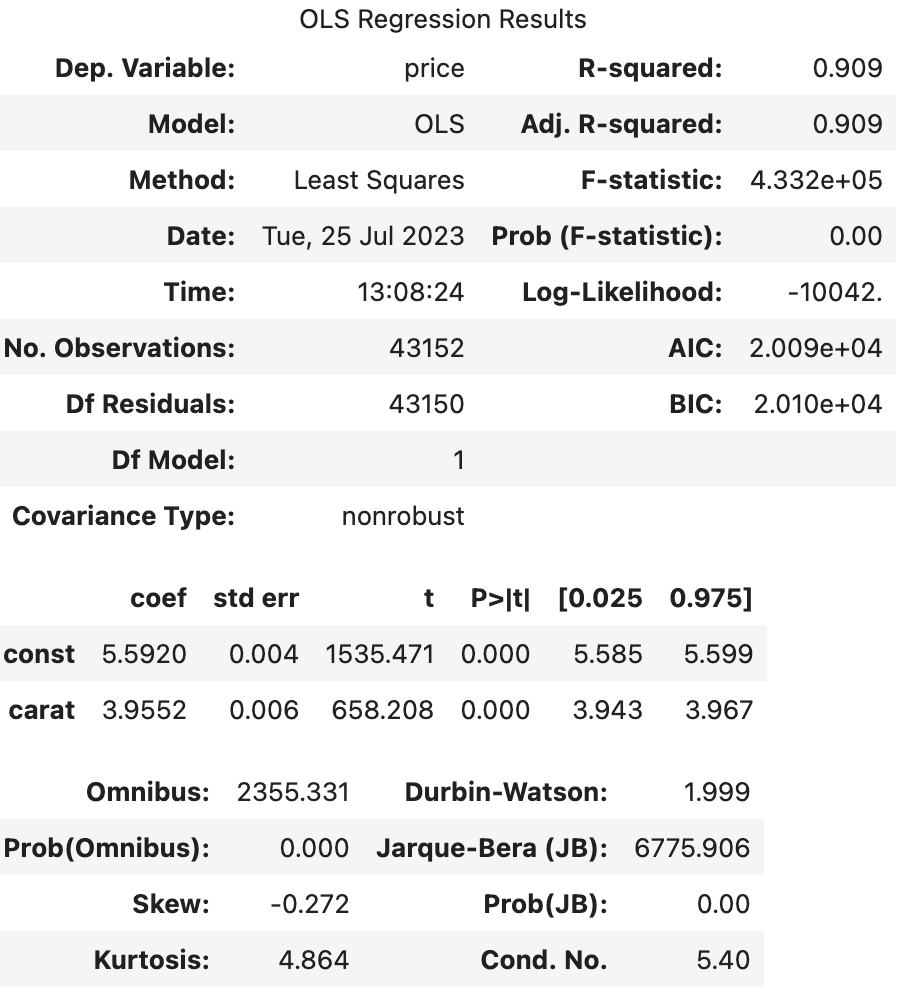
- price, carat -> log
 |  |
|---|
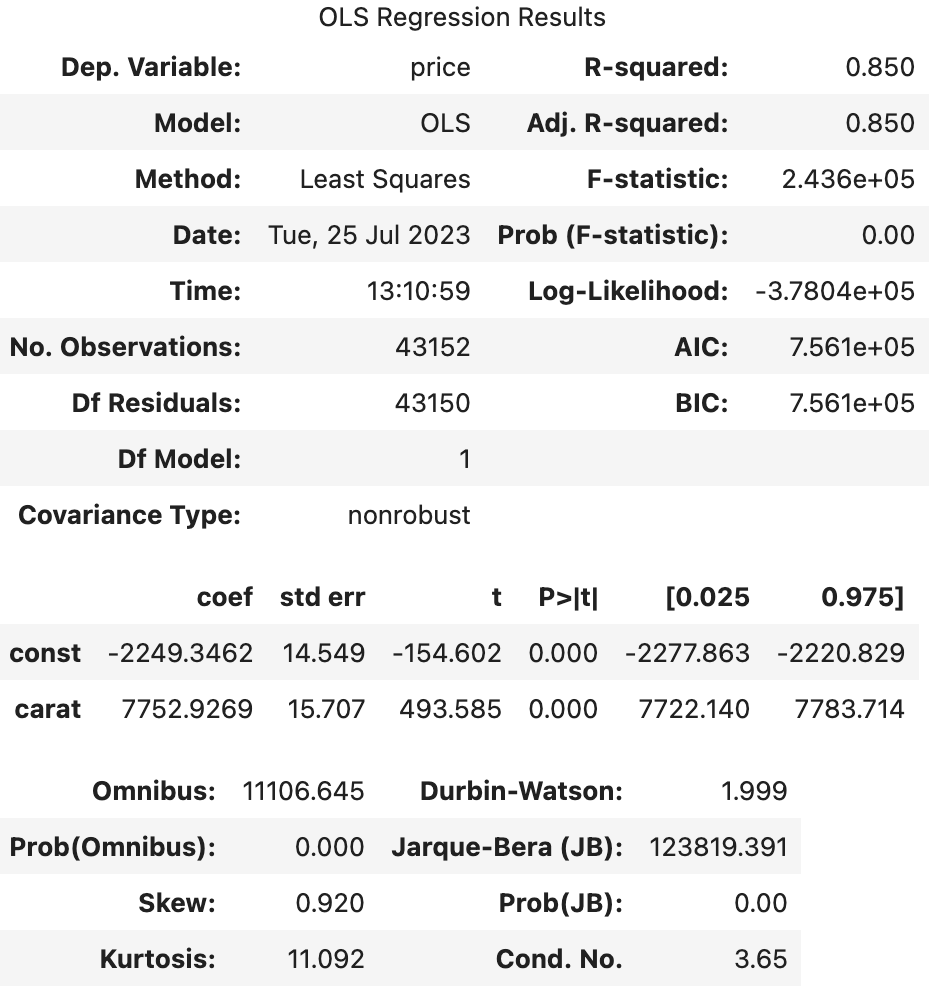
--> 유의성 검정[f-test, t-test]: 전체 회귀 계수가 유의한지 검정하는 f-test, 회귀 계수 하나하나의 유의성을 검정하는 t-test 값을 확인하면 (1), (2), (3) 모두 회귀계수가 통계적으로 유의했다.
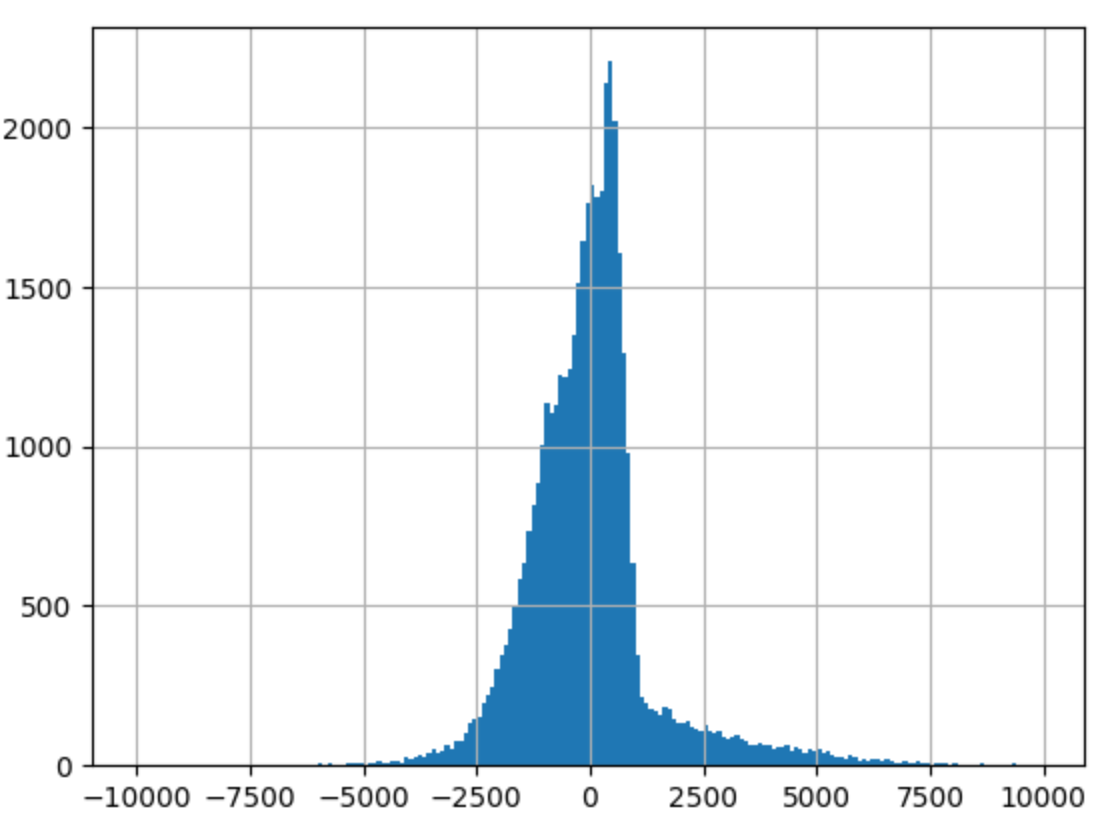
--> 종속변수와 독립변수 모두 로그를 취해주지 않았을 때(1), 독립변수만 로그를 취해주었을 때(2), 종속변수와 독립변수 모두 로그를 취해주었을 때(3)의 train 데이터의 오차 그래프를 비교해보면 (1)->(3)으로 갈수록 정규분포 모양을 하고 있었다.
실제로 그래프의 비대칭성을 나타내는 지표인 왜도(Skew)와 그래프의 뾰족한 정도를 나타내는 지표인 첨도(Kurtosis)값을 비교해보면, (3)의 왜도(Skew) 값이 0에 가장 가까우며 첨도(Kurtosis)값은 3에 가까운 것을 알 수 있다.
--> 오차항의 정규성[Omnibus,Prob(Omnibus),Jarque-Bera (JB),Prob(JB)]: (1), (2), (3) 모두 오차가 정규성을 만족하지 않는다. 따라서 위 모델을 사용하여 예측을 수행할 때에는 정규성을 만족하지 않는 잔차를 고려해야한다.
--> 오차항의 등분산성[Durbin-Watson]: (1), (2), (3) 모두 2에 가까운 값을 갖으므로 등분산성을 만족한다고 할 수 있다.
[surface area]
- price -> log / surface area
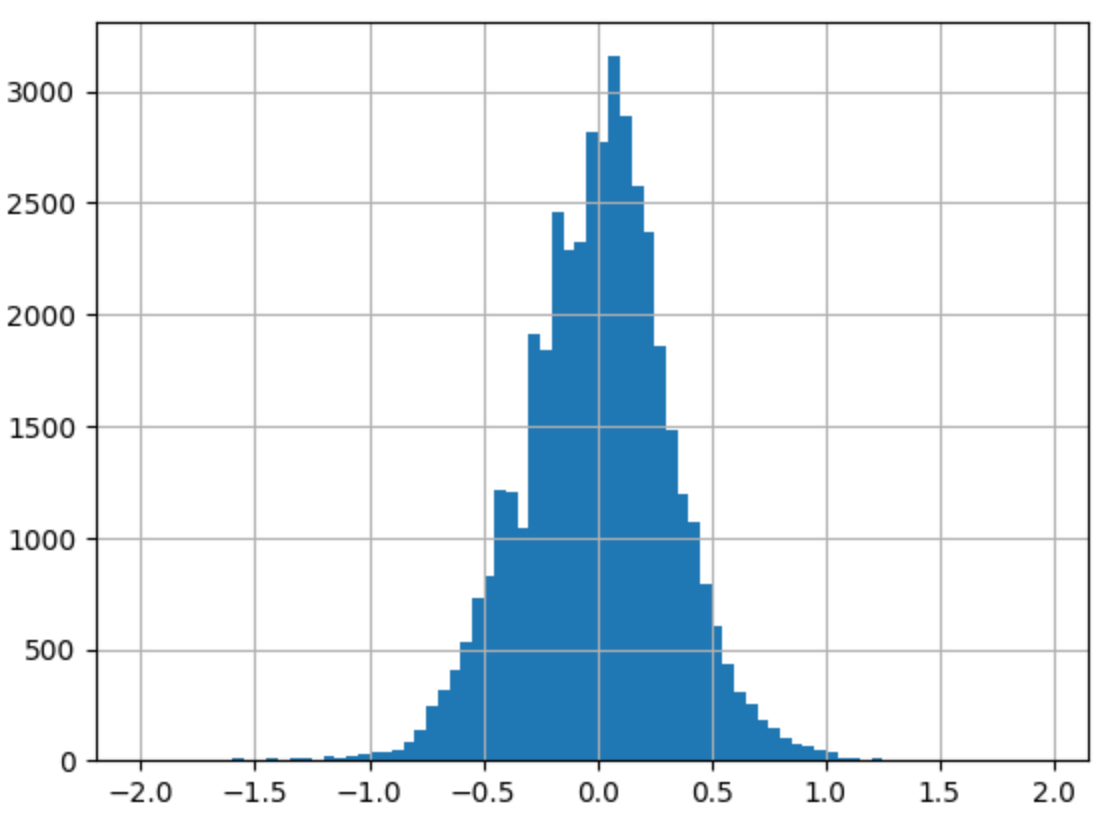 | 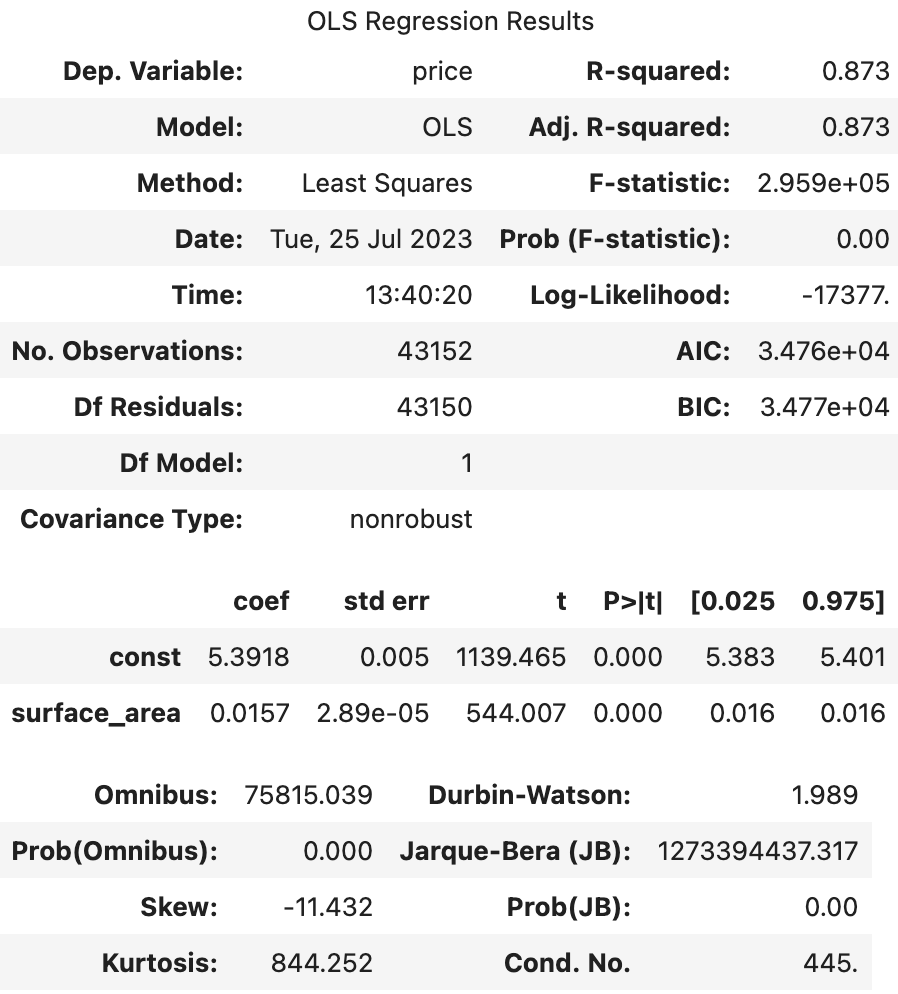 |
|---|
- price, surface area -> log
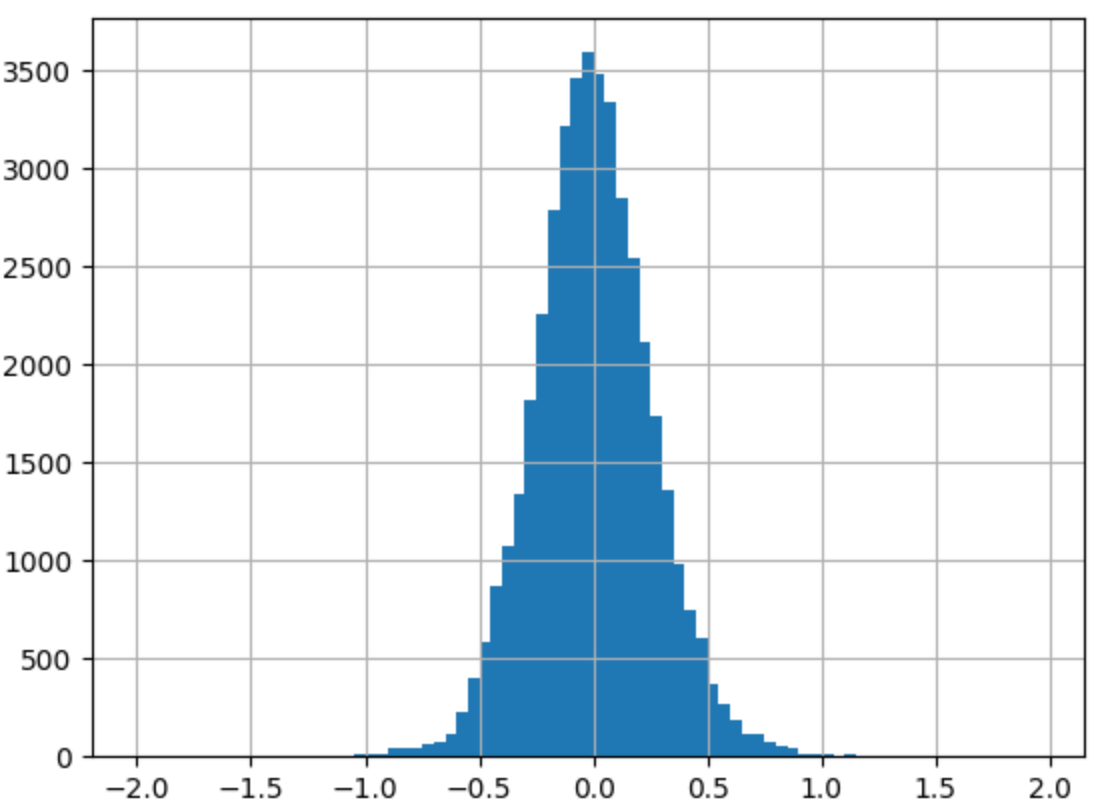 | 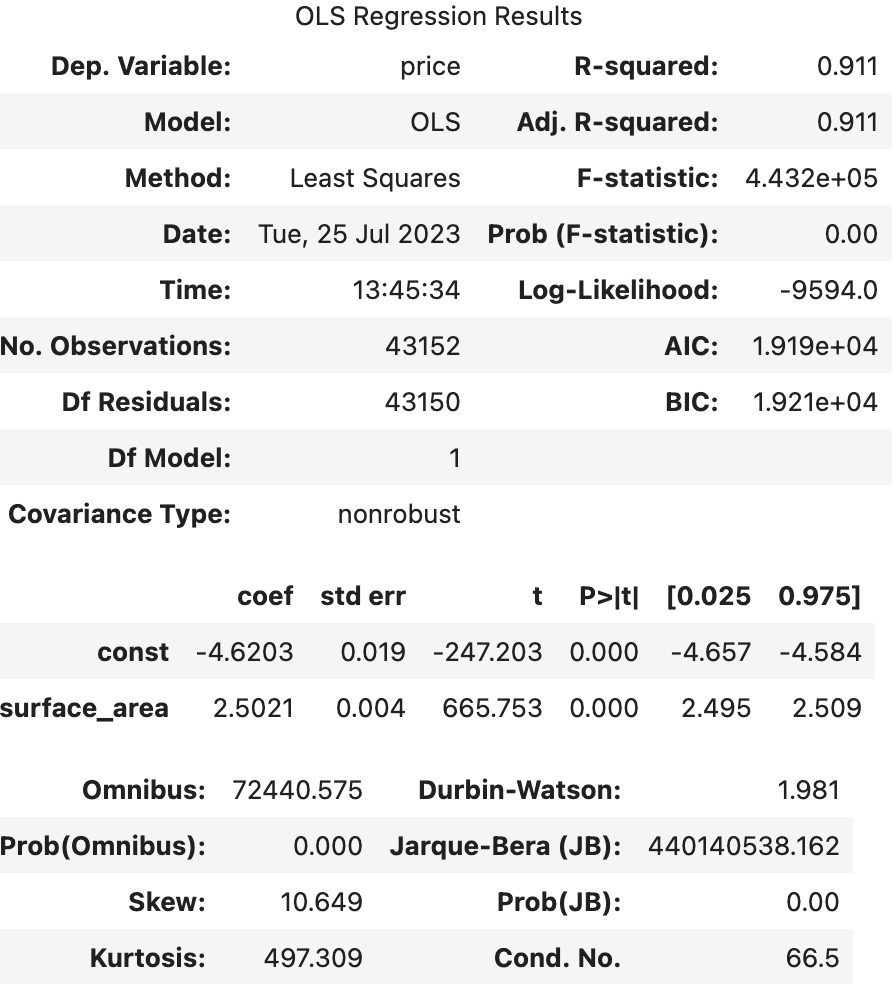 |
|---|
--> 유의성 검정[f-test, t-test]: (1), (2)의 f-test, t-test 값 모두 회귀계수가 통계적으로 유의했다.
--> 독립변수만 로그를 취해주었을 때(1), 종속변수와 독립변수 모두 로그를 취해주었을 때(2)의 train 데이터의 오차 그래프를 비교해보면 (2)가 조금 더 정규분포와 가까운 모양을 하고 있었다.
왜도(Skew), 첨도(Kurtosis)를 보면 (1), (2) 모두 한쪽으로 약간 비대칭하며 정규분포보다 뾰족한 모습을 갖고 있다.
--> 오차항의 정규성[Omnibus,Prob(Omnibus),Jarque-Bera (JB),Prob(JB)]: (1), (2) 모두 오차가 정규성을 만족하지 않는다.
--> 오차항의 등분산성[Durbin-Watson]: (1), (2) 모두 2에 가까운 값을 갖으므로 등분산성을 만족한다고 할 수 있다.
[volume]
- price -> log / volume
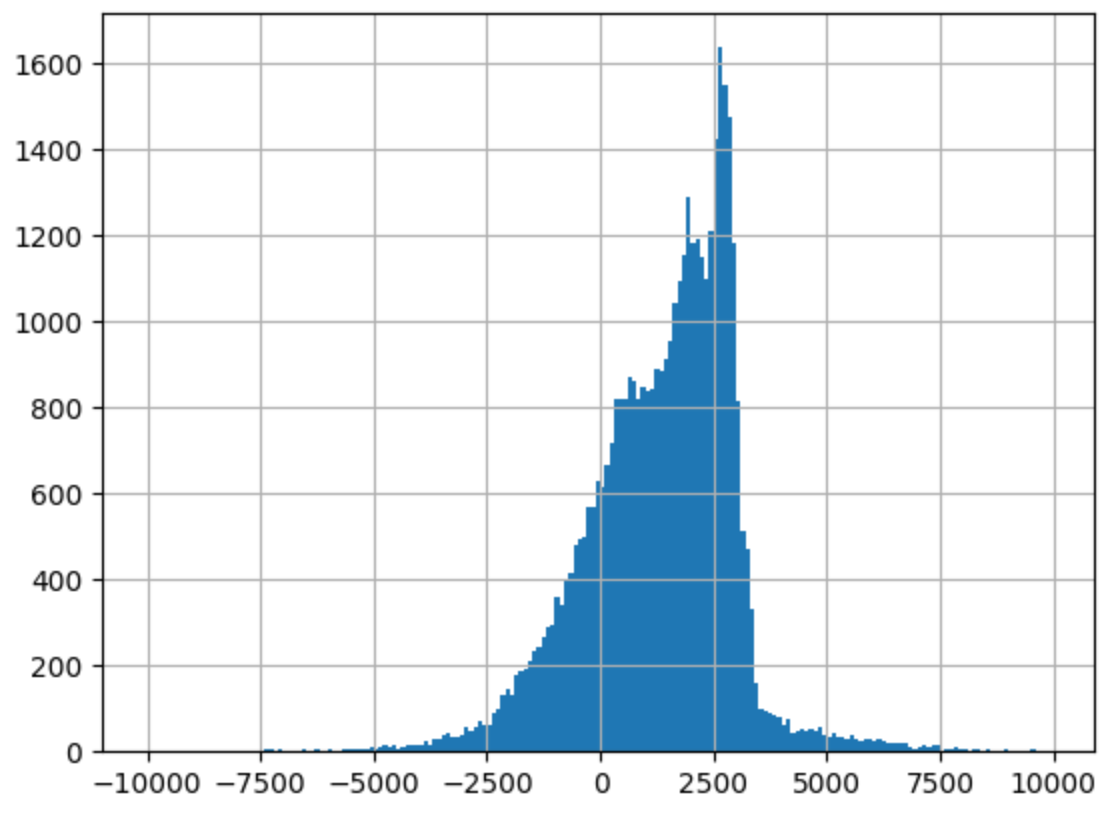 | 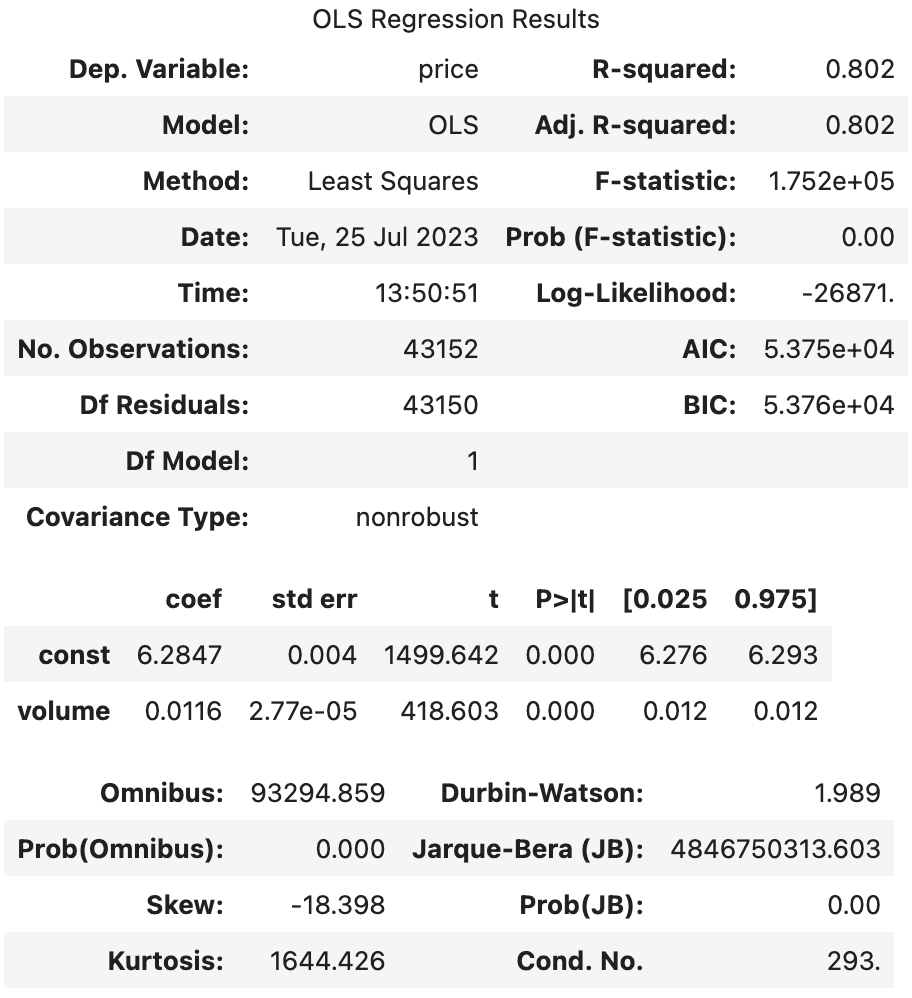 |
|---|
- price, volume -> log
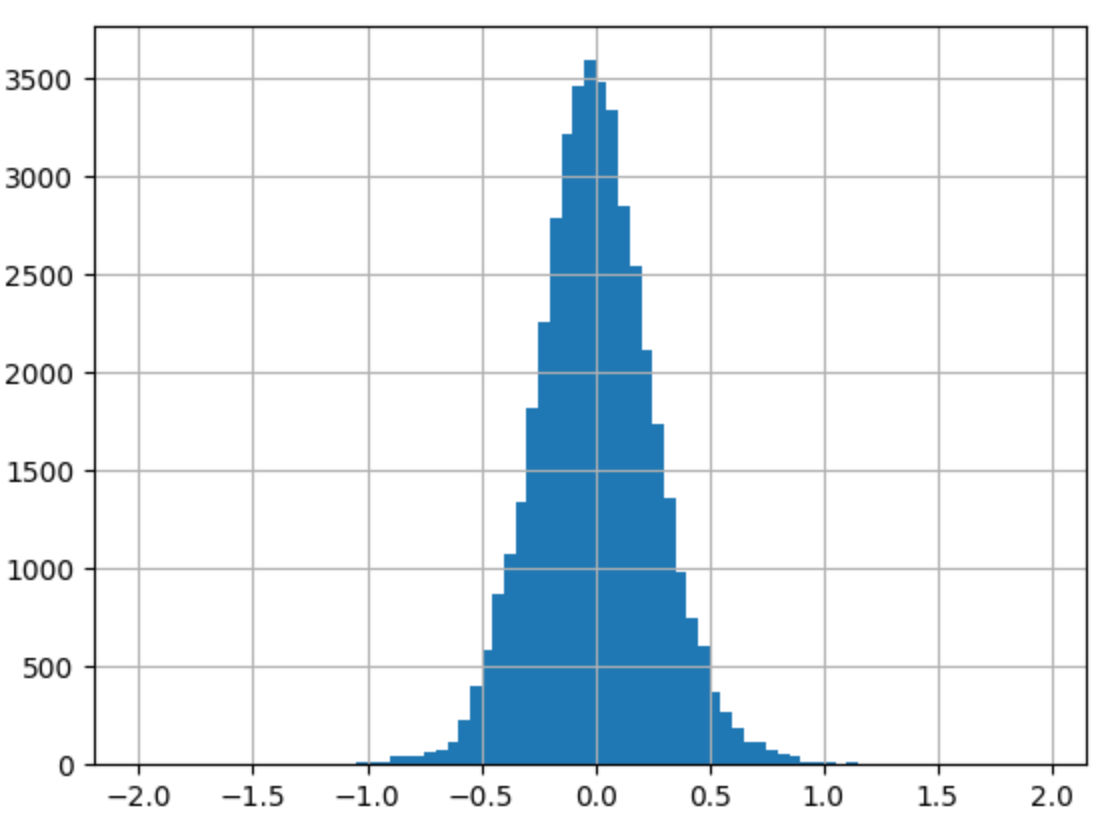 | 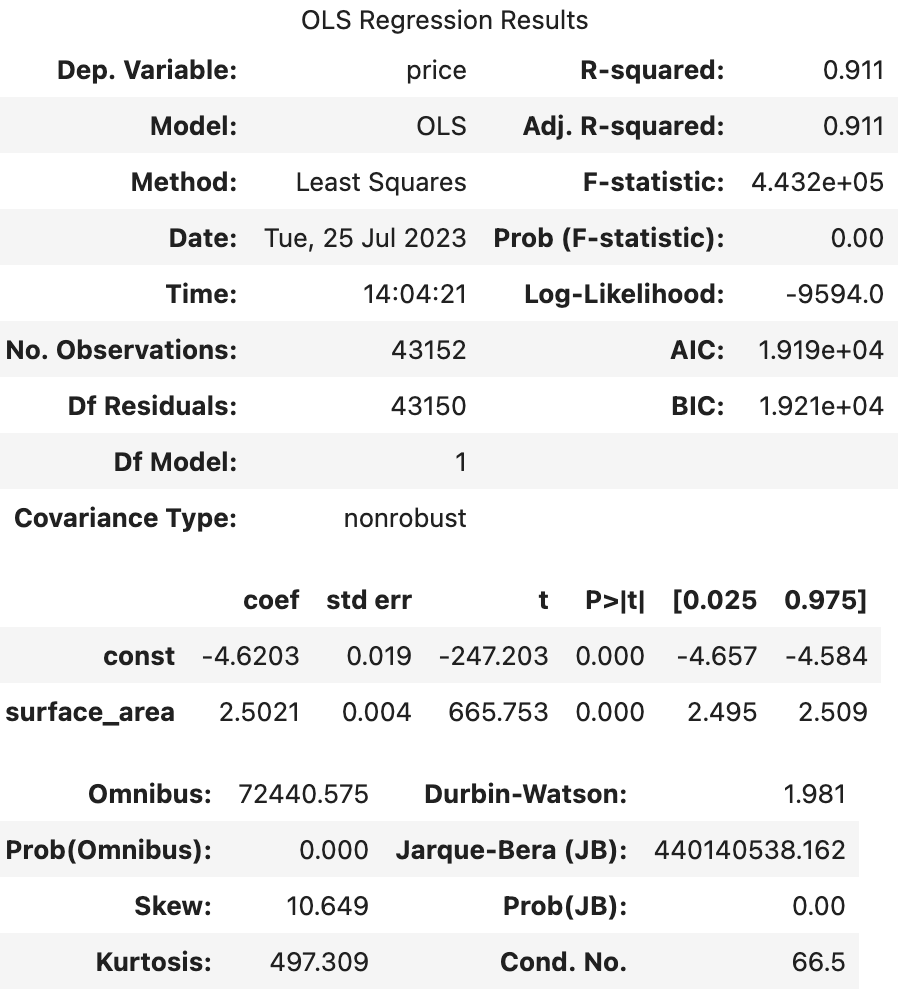 |
|---|
--> 유의성 검정[f-test, t-test]: (1), (2)의 f-test, t-test 값 모두 회귀계수가 통계적으로 유의했다.
--> 독립변수만 로그를 취해주었을 때(1), 종속변수와 독립변수 모두 로그를 취해주었을 때(2)의 train 데이터의 오차 그래프를 비교해보면 (2)가 훨씬 정규분포와 가까운 모양을 하고 있었다.
왜도(Skew), 첨도(Kurtosis)를 보면 (1), (2) 모두 한쪽으로 약간 비대칭하며 정규분포보다 뾰족한 모습을 갖고 있다.
--> 오차항의 정규성[Omnibus,Prob(Omnibus),Jarque-Bera (JB),Prob(JB)]: (1), (2) 모두 오차가 정규성을 만족하지 않는다.
--> 오차항의 등분산성[Durbin-Watson]: (1), (2) 모두 2에 가까운 값을 갖으므로 등분산성을 만족한다고 할 수 있다.
