알고리즘 자료구조ㅣ그래프, 인접행렬, 인접 리스트

그래프(Graph)

그래프

그래프 관련 문제를 풀 때는, 문제 상황을 그래프로 모델링한 후에 푸는 것이 보편적이다.

그래프란, 노드(Node)와 간선(Edge)로 연결관계를 표현한 자료구조이다.
노드는 정점(Vertex)라고 부르기도 한다.

• 노드(node) : 정점(vertex)라고도 하고, 데이터가 저장되는 그래프의 기본 우너소
• 간선(edge) : 링크(link)라고도 하고, 노드 간의 관계
• 인접 노드 : 하나의 노드에서 간선에 의해 직접 연결되어 있는 노드
• 차수(degree) : 노드에 연결된 간선의 수
• 진입 차수(in-degree) : 외부에서 오는 간선의 수
• 진출 차수(out-degree) : 외부로 향하는 간선의 수
• 경로(path) : 간선을 따라갈 수 있는 길
• 경로의 길이(length) : 경로를 구성하는 데 사용된 간선의 수
• 단순 경로(simple path) : 경로 중에 반복되는 간선이 없는 경로
• 사이클(cycle) : 시작 노드와 종료 노드가 같은 단순 경로

그래프의 종류

• 가중치가 없는 무방향 그래프
• 가중치가 있는 무방향 그래프
• 가중치가 있는 유방향 그래프

그래프의 구현

그래프를 구현하는 방법에는 인접행렬(Adjacency Matrix)와 인접리스트(Adjacency List)가 있다.

• 인접행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
• 인접리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식

인접행렬(Adjacency Matrix)

인접행렬

인접행렬은 그래프의 연결 관계를 '이차원 배열'로 나타내는 방식이다.
노드의 개수가 n이라면, n*n 형태의 2차원 배열로 그래프의 연결 관계를 표현한다.
인접 행렬을 adj[][] 라고 하면, adj[i][j]에 대해서 아래와 같이 정의할 수 있는 것이다.

adj[i][j] : 노드 i에서 노드 j로 가는 간선이 있으면 1, 아니면 0
-> 만약 간선에 가중치가 있는 그래프라면, 1 대신에 가중치의 값을 직접 넣어주는 방식으로 구현할 수도 있다.

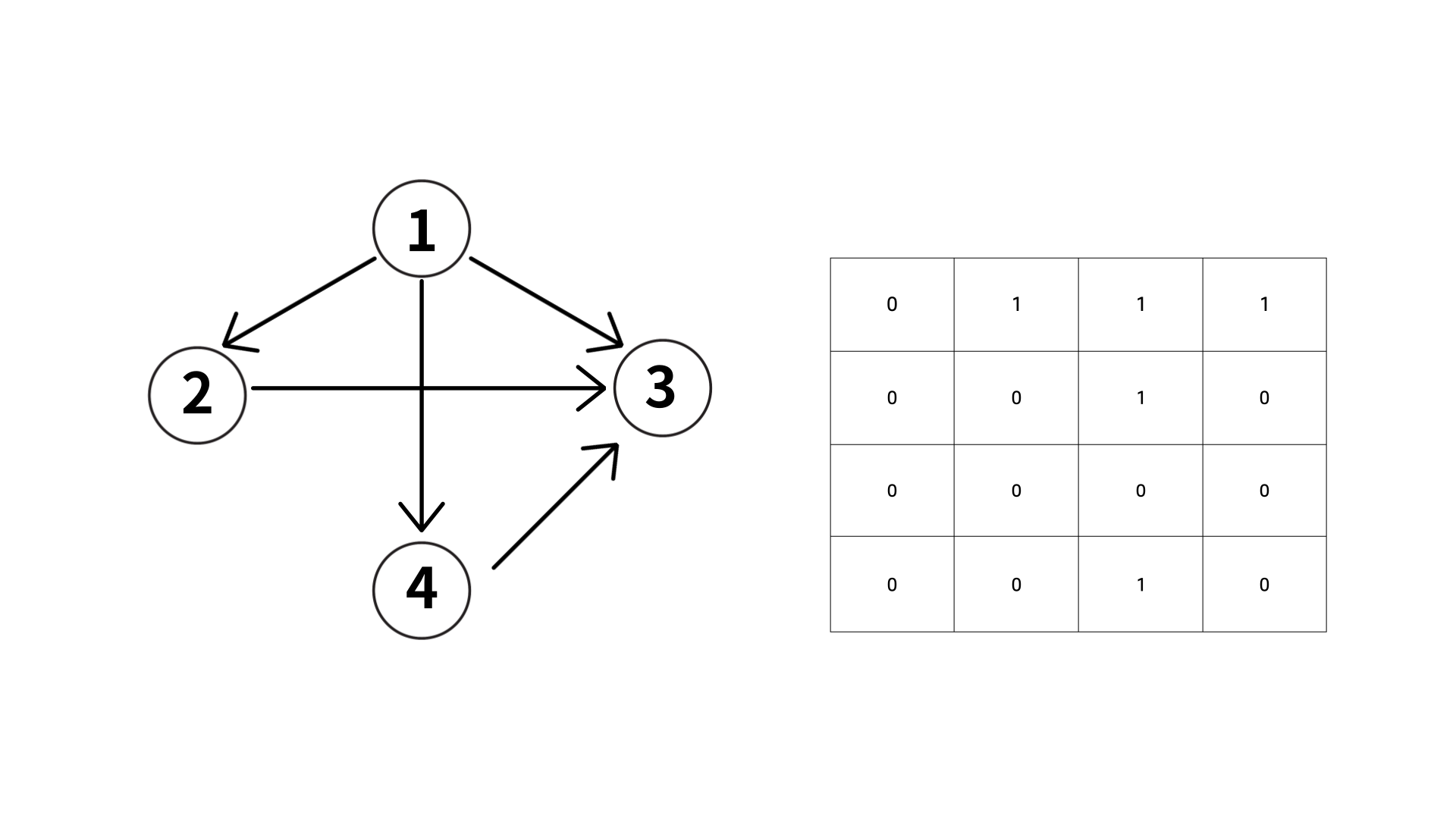
위 그림은, 왼쪽의 그래프의 연결관계를 인접행렬로 나타낸 것이다.

그러면, 간선의 방향이 있는 유향 그래프가 아닌, 간선에 방향이 없는 무향 그래프라면 어떻해야할까?

노드 i에서 노드 j로 가는 간선이 있다는 말은, 노드 j에서 노드 i로 가는 간선도 존재한다는 의미일 것이다. 따라서, 인접 행렬이 '대각 성분을 기준으로 대칭'인 성질을 갖게 된다.
예시는 아래와 같다.

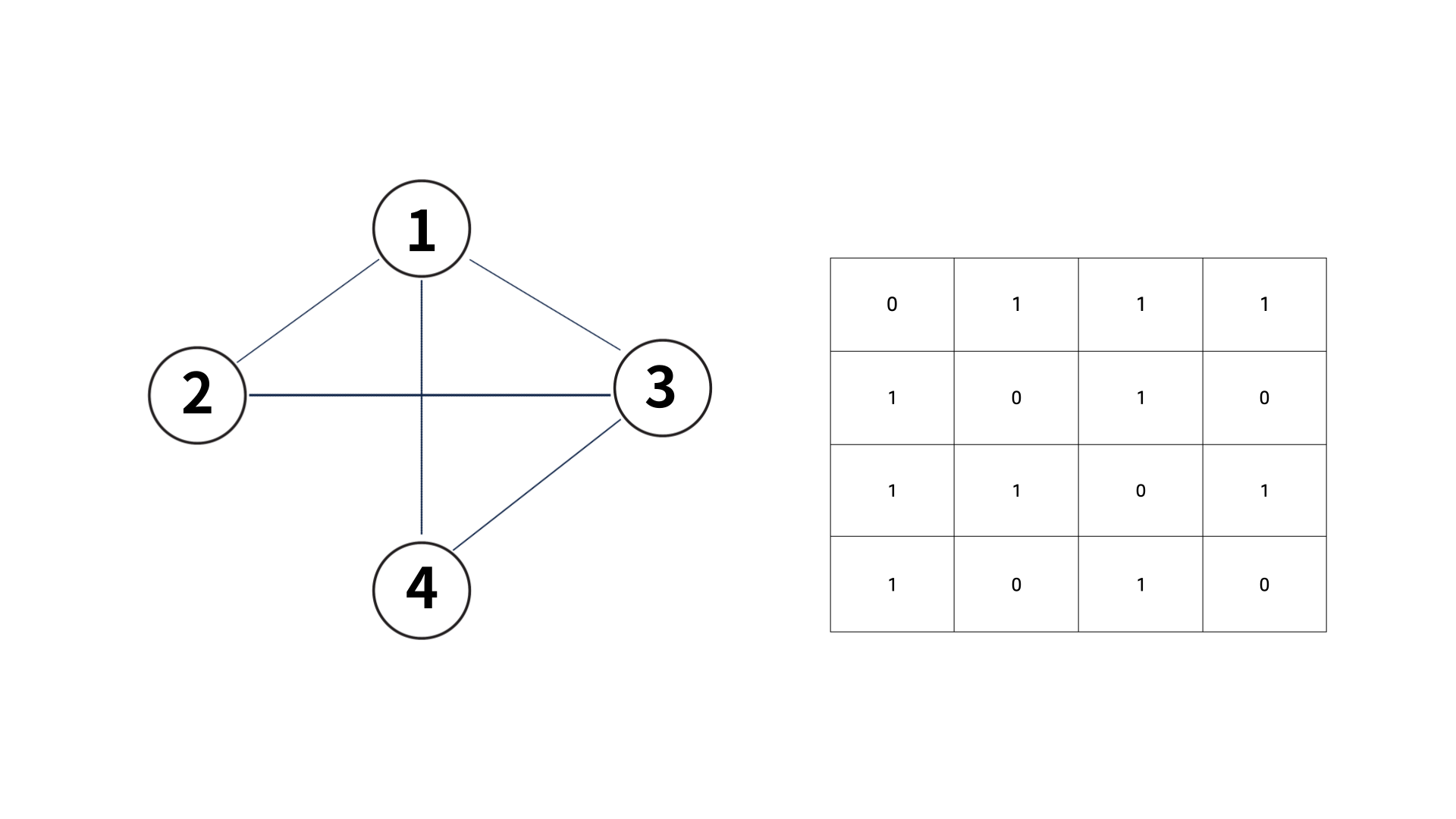
장단점

장점

• 구현이 쉽다
• 2차원 배열에 모든 노드들의 간선 정보가 있어, 두 노드를 연결하는 간선을 조회할 때 O(1) 시간복잡도를 가진다.

단점

• 전체 노드의 개수를 v개, 간선의 개수가 e라고 했을 때, 노드 i에 연결된 모든 노드들에 방문해보고 싶은 경우 adj[i][1]부터 adj[i][v]를 모두 확인해야 한다. 즉, 그래프의 모든 간선의 수를 알아내려면 인접행렬 전체를 확인해야 하므로 O(n^2)의 시간이 걸린다.
  -> 예시로 든 그래프에서는 못 느낄 수 있지만, 노드의 개수에 비해 간선의 개수가 훨씬 적은 그래프라면, 만약 노드의 개수는 총 1억개인데 연결된 간은 2개인 그래프가 있을 때, 특정 노드와 연결된 노드들이 몇 번 노드인지 확인하기 위해서는 총 1억 개의 노드들을 모두 확인해야 하는 치명적인 문제가 발생한다.
  -> 이러한 단점을 보완할 수 있는 연결 관계 표현 방식이 '인접 리스트'

인접 리스트

그래프의 각 노드에 인접한 노드들을 연결리스트(Linked List)로 표현하는 방법.

즉, 노드의 개수만큼 인접리스트가 존재하고, 각각의 인접리스트에는 인접한 노드 정보가 저장된다. 그래프는 각 인접리스트에 대한 헤드포인터를 배열로 갖는다.

• 헤드포인터 : 연결 리스트의 맨 처음 노드를 가리키는 포인터

• 가중치가 없는 무향 그래프의 경우에는 양쪽에 저장되는 것을 안 잊으면 된다.

• 가중치가 없는 무방향 그래프의 경우, 가중치 표현 없이 인접한 노드 정보가 저장된다.

• 가중치가 있는 유방향 그래프의 경우 종점[노드번호 | 간선의 가중치] 정보가 저장된다.

장단점

장점

• 인접 행렬과 달리, 실제로 연결된 노드들에 대한 정보만 저장하기 때문에 모든 벡터들의 원소의 개수의 합이 간선의 개수와 같다는 점. 즉, 간선의 개수에 비례하는 메모리만 차지, 쉽게, 존재하는 간선만 관리하므로 메모리 사용이 효율적이다.

단점

• 두 노드를 연결하는 간선을 조회하거나 노드의 차수를 알기 위해서는 노드의 인접 리스트를 탐색해야 해서 노드의 차수만큼의 시간이 필요하다.
  -> 노드 i와 노드 j가 연결되어 있는지 알고 싶은 경우, adj[i]의 벡터 전체를 돌며, j를 성분으로 갖는지 확인해야 한다. 인접행렬의 경우 adj[i][j]가 1인지 0인지만 확인하면 되어 O(1)의 시간 복잡도인데 말이다.

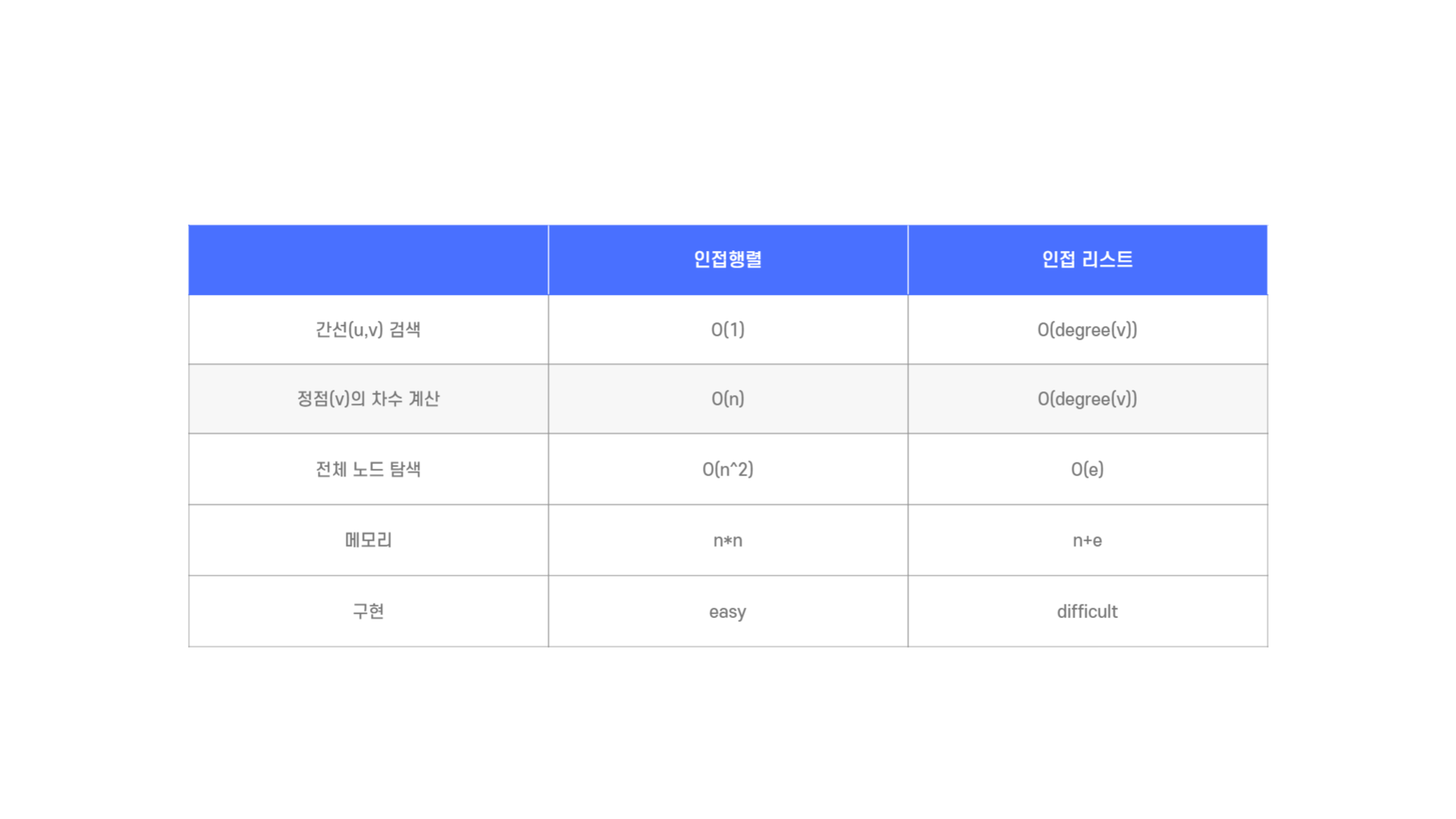
무엇이 좋다, 나쁘다가 아닌, 문제에 따라 적절한 표현방식을 이용해 연결 관계를 저장하는 것이 중요하다.