비선형 자료 구조
비선형 자료 구조
'비선형 자료 구조'란, 일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조를 뜻한다.
일반적으로 트리나 그래프가 있다.
그래프
그래프
그래프는 '정점'과 '간선'으로 이루어진 자료 구조이다.
정점과 간선
어떠한 곳에서 어떠한 곳으로 무언가를 통해 간다고 했을 때, '어떠한 곳'은 정점(vertex)이고, '무언가'는 간선(edge)이다.
A라는 개발자가 B라는 엄마를 보러간다고 했을 때, A라는 개발자와 B라는 엄마는 '정점'이고, 엄마를 보러가는 길은 '간선'이되는 것이다.
만약 A라는 사람이 B라는 사람을 좋아하는데 '짝사랑'이라면, '단방향 간선'이 될 것이다.
하지만 B라는 사람도 A를 좋아한다면, '양방향 간선'인 것이다.
정점으로 나가는 간선은 해당 정점의 outdegree라고 하고, 들어오는 간선을 해당 정점의 indegree라고 한다. 또한, 정점은 약자로 V 또는 U라고 하는데, 보통 어떤 정점으로부터 어떤 정점까지 가는 것을 "U에서 V로 간다"라고 표현한다. 그리고 정점과 간선으로 이루어진 집합을 '그래프(graph)'라고 한다.
가중치
'가중치'는 간선과 정점 사이에서 드는 비용을 말한다. 1번 노드와 2번 노드까지 가는 비용이 한 칸이라면, 1번 노드에서 2번 노드까지의 가중치는 한 칸인 것이다.
트리
트리
'트리'는 그래프 중 하나이고, 그래프의 특징처럼 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 '계층적 데이터의 집합'이다. 루트 노드, 내부 노드, 리프 노드 등으로 구성된다.
트리의 특징
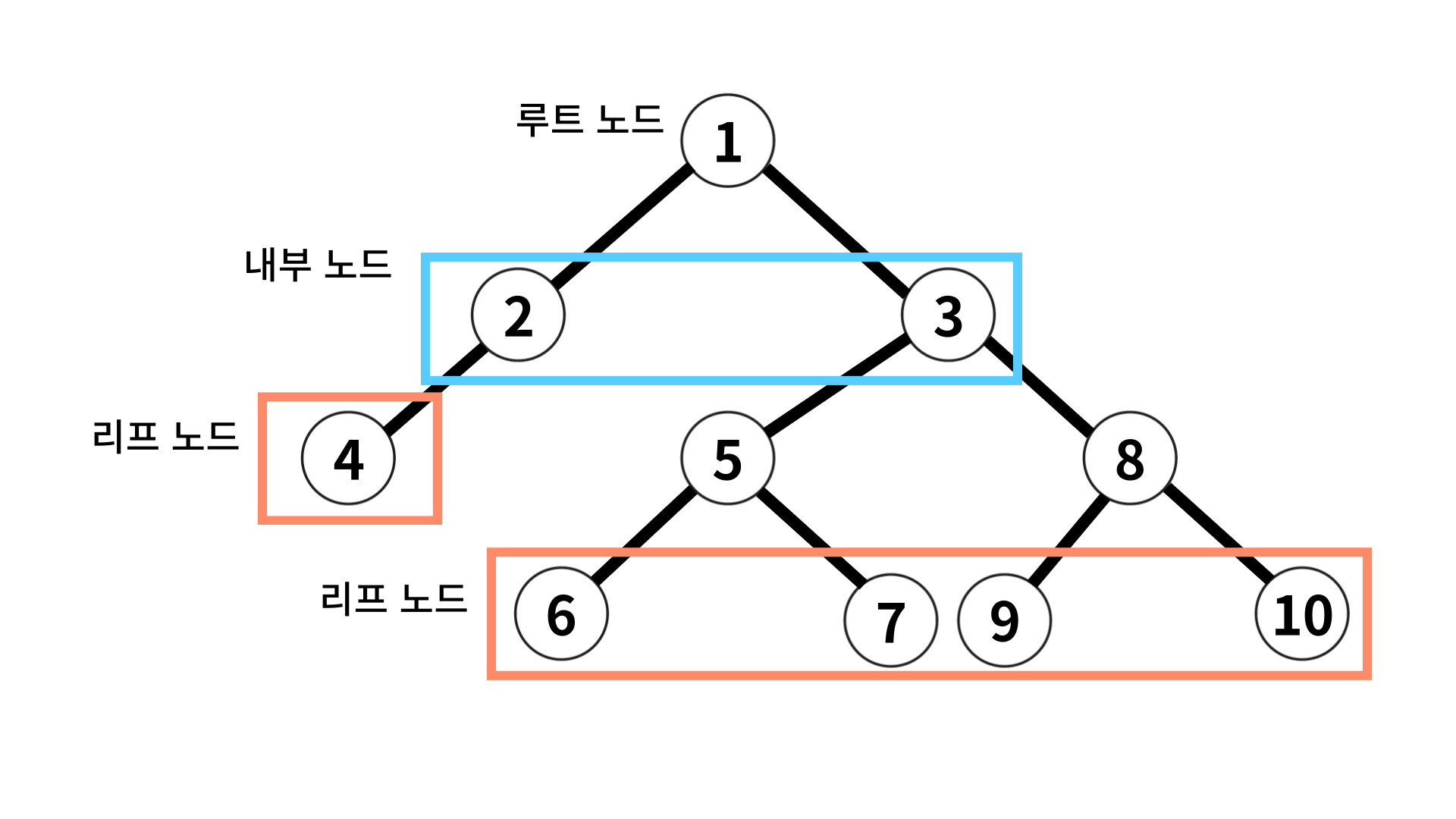
위와 같은 트리는 그래프의 일종이며, 아래와 같은 특징을 가진다.
-
부모, 자식 계층 구조를 가진다. 5번 노드는 6,7번 노드의 부모 노드이고, 6,7번 노드는 5번 노드의 자식 노드이다. 같은 경로상에서 어떤 노드보다 위에 있으면 부모, 아래 있으면 자식 노드가 되는 것이다.
-
V-1=E, 즉, 간선 수는 노드 수-1이다.
-
임의의 두 노드 사이의 겨로는 '유일무이'하게 '존재'한다. 즉, 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 있다.
트리의 구성
트리는 루트 노드, 내부 노드, 리프 노드로 이루어져 있다.
루트 노드
가장 위에 있는 노드를 말한다.
내부 노드
루트 노드와 내부 노드 사이에 있는 노드를 말한다.
리프 노드
리픈 노드는 자식 노드가 없는 노드를 말한다.
트리의 높이와레벨
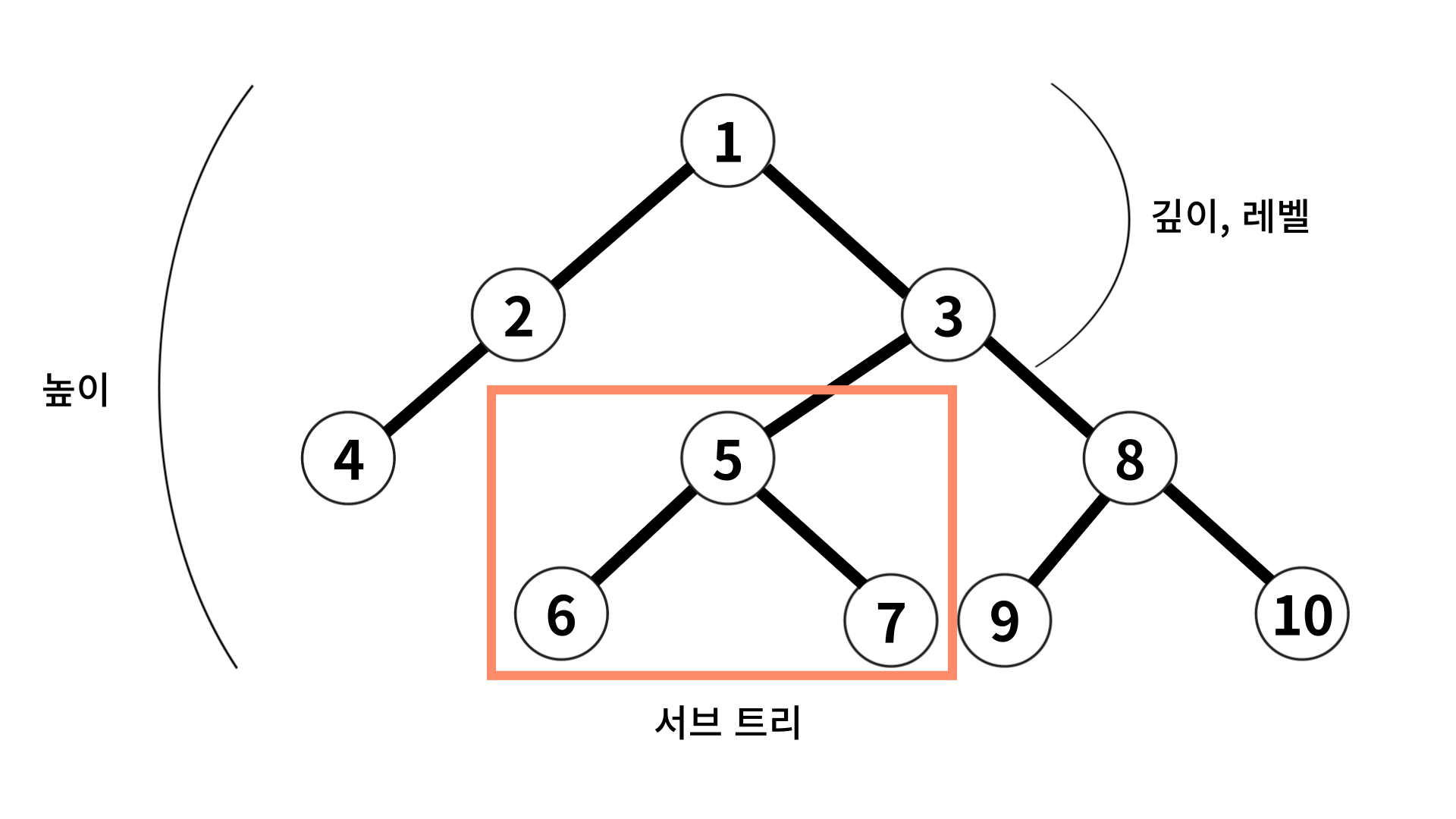
-
깊이 : 트리에서의 깊이는 각 노드마다 다르고, 루트 노드부터 특정 노드까지 '최단 거리'로 갔을 때의 거리를 말한다. 4번 노드의 깊이는 2이다.
-
높이 : 트리의 높이는 루트 노드부터 리프 노드까지 거리 중 '가장 긴 거리'를 말하고, 위 그림의 트리 높이는 3이다.
-
레벨 : 트리의 레벨은 주어지는 문제마다 조금씩 다르지만, 보통 깊이와 같은 의미를 지닌다.
-
서브트리 : 트리 내의 하위 집합을 서브트리라고 한다. '트리 내에 있는 부분집합'이라고 생각하면 쉽다.
이진 트리
'이진 트리'는, 자식의 노드 수가 2개 이하인 트리를 말하고, 자세히는 아래와 같이 분류한다.
-
정이진 트리(full binary tree) : 자식 노드가 0개 또는 2개인 이진 트리
-
완전 이진 트리(complete binary tree) : 왼쪽에서부터 채워져 있는 이진 트리를 말한다. 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 경우 왼쪽부터 채워져 있다.
-
변질 이진 트리(degenerate binary tree) : 자식 노드가 하나밖에 없는 이진 트리
-
포화 이진 트리(perfect binary tree) : 모든 노드가 꽉 차 있는 이진 트리
-
균형 이진 트리(balanced bianry tree) : 왼쪽과 오른쪽 노드의 높이 차이가 1이하인 이진 트리를 말하며, map, set을 구성하는 레드 블랙 트리는 균형 이진 트리 중 하나이다.
이진 탐색 트리
이진 탐색 트리(BST)는, 노드의 오른쪽 하위 트리에는 '노드 값보다 큰 값'이 있는 노드만 포함하고, 왼쪽 하위 트리에는 '노드 값보다 작은 값'이 들어 있는 트리를 말한다.
아래와 같이 말이다.
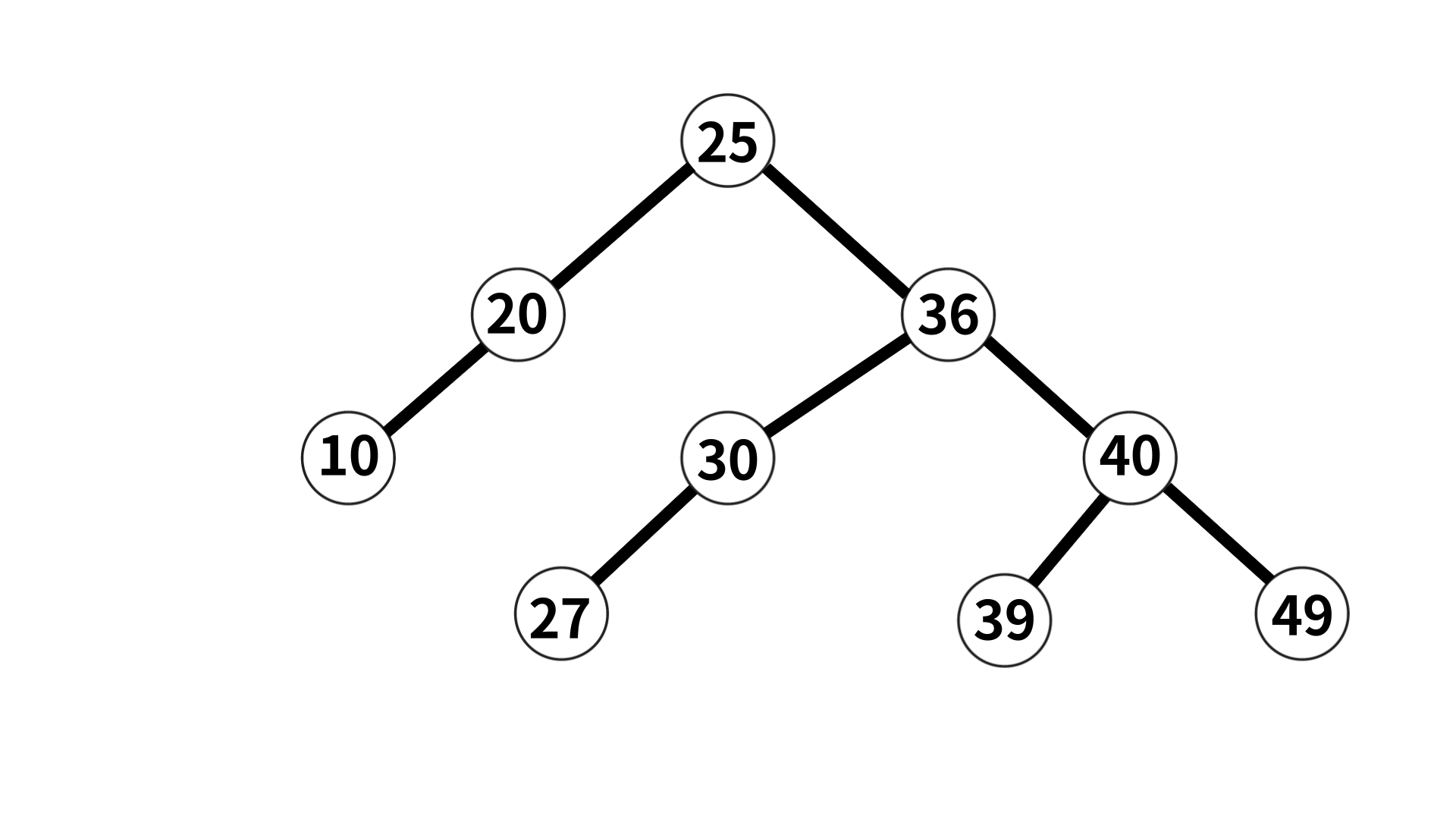
이 때, 왼쪽 및 오른쪽 하위 트리도 해당 특성을 지닌다. 이렇게 하면 '검색'을 하기에 매우 편리하다. 왼쪽에는 작은 값, 오른쪽에는 큰 값이 이미 정해져 있기 때문에 10을 찾는다고 하면 25의 왼쪽 노드들만 찾으면 되기 때문이다. 보통 요소를 찾을 때 이진 탐색 트리의 경우 O(logn)이 걸린다. 하지만 최악의 경우에는 O(n)이 걸릴 수도 있다.
이유는, 이진 트리는 삽입 순서에 따라 선형적일 수도 있기 때문이다.
AVL 트리
AVL트리(Adelson-Velsky and Landis tree)는 위에 설명한 최악의 경우 선형적인 트리가 되는 것을 방지하고, 스스로 균형을 잡는 이진 탐색 트리이다. 두 자식 서브트리의 높이가 항상 최대 1만큼 차이가 나는 특징이 있다.
이진 탐색 트리는 선형적인 트리 형태를 가질 때는 최악의 경우 O(n)의 시간 복잡도를 가진다고 햇는데, AVL트리는 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)이고, 삽입, 삭제를 할 때마다 균형이 안 맞는 것을 맞추기 위해 트리 일부를 왼쪽 혹은 오른쪽으로 회전시키며 균형을 잡는다.
레드 블랙 트리
'레드 블랙 트리'는, 균형 이진 탐색 트리로, 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)이다. 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트를 저장하고, 삽입 및 삭제 중 트리가 균형을 유지하도록 하는데 사용된다. C++ STL의 set, multiset, map, and multimap이 레드 블랙 트리를 이용하여 구현되어 있다.
모든 리프 노드와 루트 노드는 블랙이고, 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다 라는 등의 규칙을 기반으로 균형을 잡는 트리이다.
힙
힙
'힙'은, 완전 이진 트리 기반의 자료 구조이고, '최소힙'과 '최대힙' 2가지가 있고, 해당 힙에 따라 특정한 특징을 지킨 트리를 뜻한다.
- 최대힙
: 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 한다. 또한, 각 노드의 자식 노드와의 관계도 이와 같은 특징이 재귀적으로 이루어져야 한다. - 최소힙
: 최소힙에서 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 최솟값이어야 한다. 또한, 각 노드의 자식 노드와의 관계도 이와 같은 특징이 재귀적으로 이루어져야 한다.
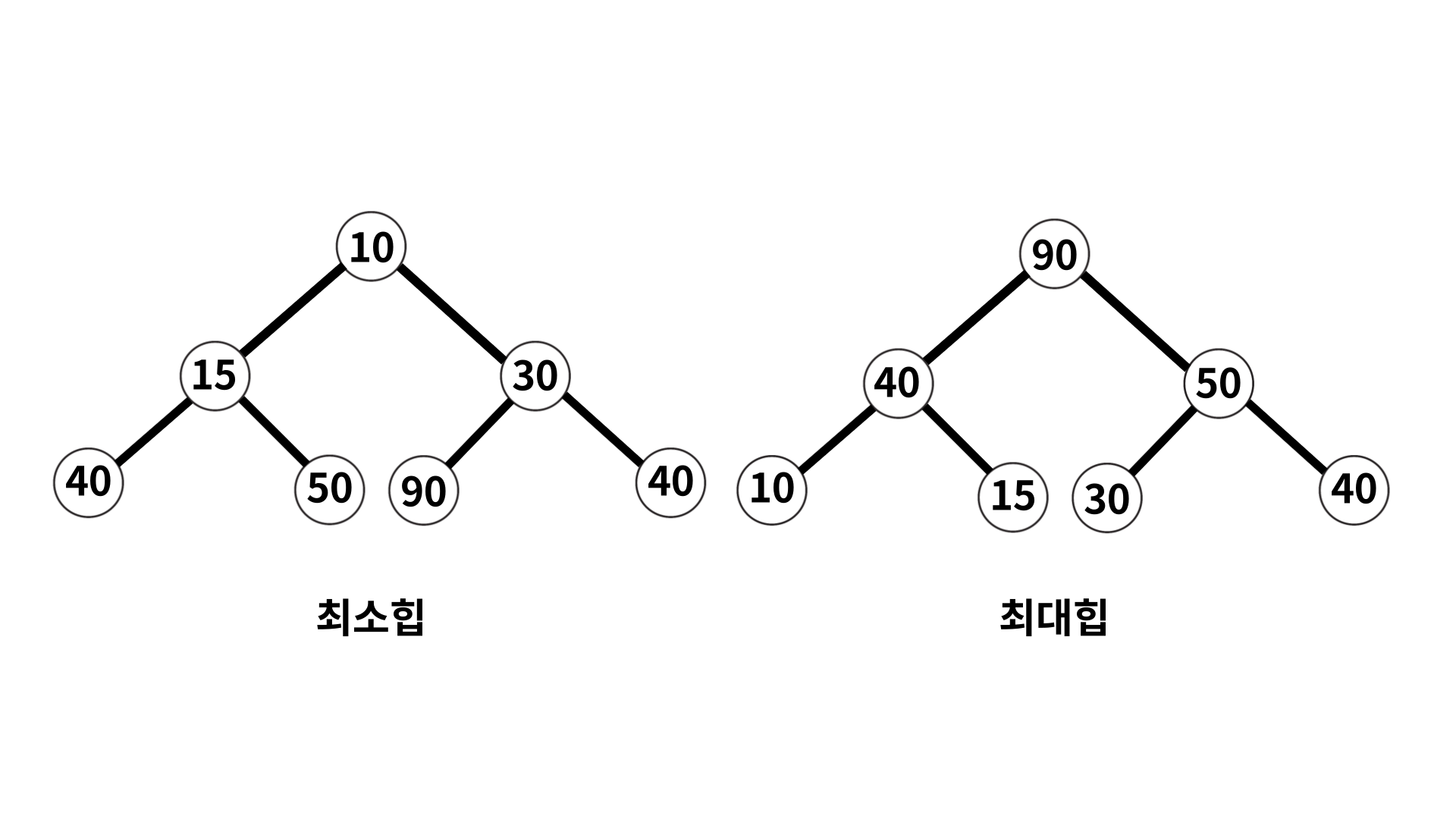
힙에는 어떤 값이 들어와도 특정 힙의 규칙을 지키게 만들어져 있다. 만약 최대힙을 기반으로 설명하면 아래와 같다.
최대힙의 삽입
힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다. 그리고 새로운 노드를 부모 노드들과의 크기를 비교하며 교환해서 힙의 성질을 만족시키게 된다.
만약 7이라는 값을 가진 노드 밑에 13이라는 값을 가진 노드를 삽입한다고 하면, 이 노드가 점차 올라가면서 해당 노드 위에 있는 노드와 스왑하는 과정을 거쳐 최대힙 조건을 결국엔 만족하게 된다.
최대힙의 삭제
최대힙에서 최댓값은 루트 노드이다. 따라서 루트 노드가 삭제되고, 그 이후 마지막 노드와 루트 노드를 스왑하여 또다시 스왑 등의 과정을 거쳐 재구성되게 된다.
우선순위 큐
우선순위 큐
'우선순위 큐'는, 우선순위 대기열이라고도 한다. 대기열에서 우선순위가 높은 요소가 우선 순위가 낮은 요소보다 먼저 제공되는 자료 구조이다.
우선순위 큐는 '힙'을 기반으로 구현된다.
아래 코드처럼 greater를 써서 오름차순, less를 사용해 내림차순으로 바꿀 수도 있다. int뿐 아니라 다른 자료 구조를 넣어서 할 수도 있다.
C++
using namespace std;
priority_queue<int, vector<int>, greater<int>> pq;
// priority_queue<int, vector<int>, less<int>> pq;
int main(){
pq.push(5);
pq.push(4);
pq.push(3);
pq.push(2);
pq.push(1);
cout << pq.top() << "\n";
return 0;
}
/*
1
*/오름차순으로 정렬한 것을 알 수 있고, 5,4,3,2,1 순으로 입력되었지만 우선순위가 높은 1이 출력된 것을 알 수 있다.
맵(Map)
맵(Map)
'맵(map)'은 특정 순서에 따라 키와 매핑된 값의 조합으로 형성된 자료 구조이다. 만약 "홍길동":1, "김민지":2 와 같은 방식으로 string:int 형태로 값을 할당해야 할 때가 있다면, 이럴 때 map을 쓰는 것이다. 레드 블랙 트리 자료 구조를 기반으로 형성되고, 삽입하면 자동으로 정렬된다.
맵을 쓸 때는 map<string, int> 형태로 구현한다. 배열과 비슷하게 clear() 함수로 맵에 있는 모든 요소를 삭제할 수 있고, size()로 map 크기를 구할 수 있다. 또한, erase()로 해당 키와 키에 매핑된 값을 지울 수도 있다.
참고로 map은 해시 테이블을 구현할 때 쓰며, 정렬을 보장하지 않는 unordered_map과 정렬을 보장하는 map, 2가지가 있다.
map을 순회할 때는 키에 해당하는 값(key)을 first, 키에 매핑된 값(value)에 해당하는 값을 second로 탐색 가능하다.
셋(Set)
셋(Set)
셋(Set)은, 특정 순서에 따라 고유한 요소를 저장하는 컨테이너이다. 중복되는 요소는 없고 오로지 희소한(unique) 값만 저장하는 자료 구조이다. 나머지는 map과 비슷하다.
해시테이블
해시 테이블
'해시 테이블'은, 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블이다. 삽입, 삭제, 탐색 시 평균적으로 O(1)의 시간 복잡도를 가지고, unordered_map으로 구현한다.

