알고리즘 자료구조ㅣBFS(너비우선탐색), DFS(깊이우선탐색)

BFS, DFS는 그래프를 탐색하는 방법이다.
그래프를 탐색한다는 것은, 하나의 정점으로부터 시작해 차례대로 모든 정점들을 한 번씩 방문한다는 것이다.

DFS(Depth First Search) - 깊이 우선 탐색

DFS

: 최대한 깊이 내려가다가, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동

Stack or 재귀함수로 구현한다.

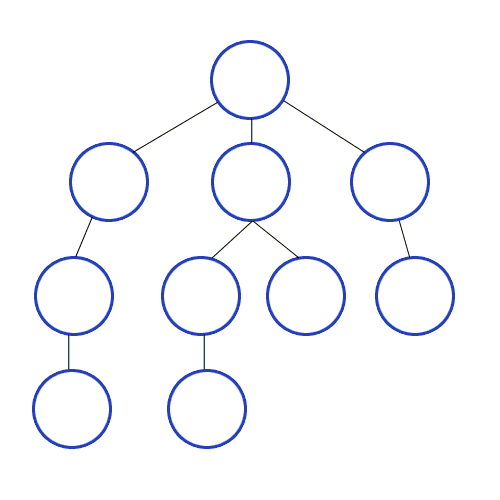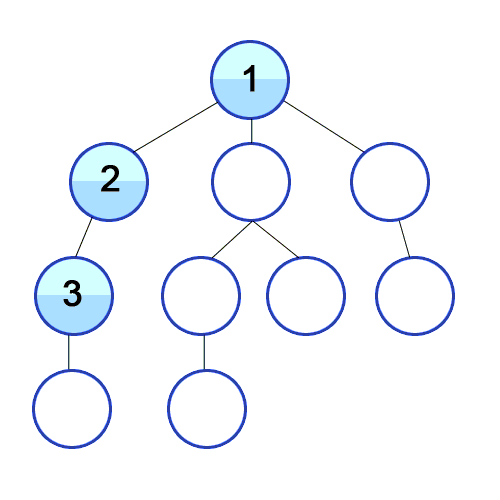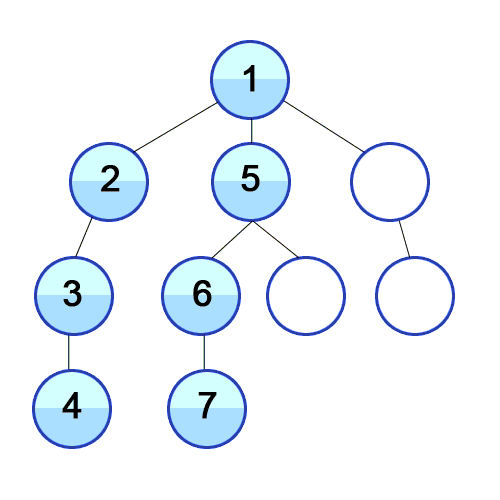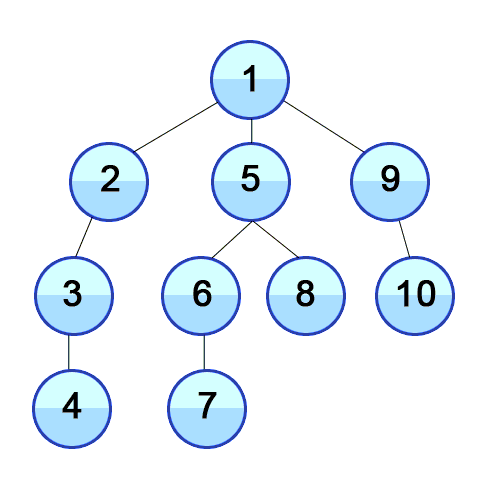
출처 : https://developer-mac.tistory.com/64

DFS의 개념

Root Node 혹은 어떠한 Node에서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.

쉽게 생각했을 때, 누군가를 찾기 위해 최대한 한 방향으로 갈 수 있을 때까지 가다가, 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아가서 다시 다른 방향으로 진행하는 것이 DFS라고 할 수 있다.

• 모든 노드를 방문하고싶을 때 DFS 활용
• DFS가 BFS보다 좀 더 간단
• 검색 속도 자체는 BFS에 비해서 느리다.
• 트리의 경우, 왼쪽에 위치한 노드를 우선적으로 탐색
• 그래프의 경우, 가중치 또는 특정 기준을 따라 탐색 방향의 우선순위를 결정

DFS 과정

DFS는 일반적으로 재귀 함수로 구현되며, 과정은 아래와 같다.

1. 왼쪽에 위치한 노드를 우선적으로 탐색
2. 해당 위치의 노드가 null이라면 이전 케이스로 돌아온다.
3. 오른쪽 노드를 탐색한다
4. 이를 재귀적으로 반복

DFS 적용 경우

DFS는 사이클(순환)의 존재 여부를 확인할 때 사용

DFS가 사이클 여부 확인할 때 사용되는 이유는, 깊이를 우선적으로 탐색하기 때문, 즉, 하나의 방향이 잡히면 그 방향의 끝에 도달할 때까지 탐색하기 때문이다. 따라서 사이클이 존재하는 방향만 찾으면 바로 사이클을 확인할 수 있다.

시간 복잡도

• 접점(V), 간선(E)
• 인접 리스트 : O(V+E)
• 인접 행렬 : O(V^2)

BFS(Breadth-First Search) - 너비 우선 탐색

BFS

: 최대한 넓게 이동한 후, 더 이상 갈 수 없을 때 아래로 이동

출처 : https://developer-mac.tistory.com/64

BFS 탐색 개념

Root Node 혹은 다른 Node에서 인접한 노드를 먼저 탐색하는 방법으로, 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.

주로 '두 노드 사이의 최단 경로'를 찾고 싶을 때 사용한다.

ex) 대한민국 국민의 관계를 가진 그래프에서 민수와 민지 사이에 존재하는 경로를 찾는 경우

• DFS - 모든 관계를 다 살펴봐야 할지 모른다
• BFS - 민수와 가까운 관계부터 탐색

BFS는 DFS와는 다르게, 끝까지 파고드는 것이 아닌, 주변을 순차적으로 확인하는 방식이다.

• 트리의 경우, 현재 위치의 좌/우 자식 노들르 순차적으로 탐색
• 그래프의 경우, 가중치 또는 특정 기준에 따라 순차적으로 연결된 노드를 탐색

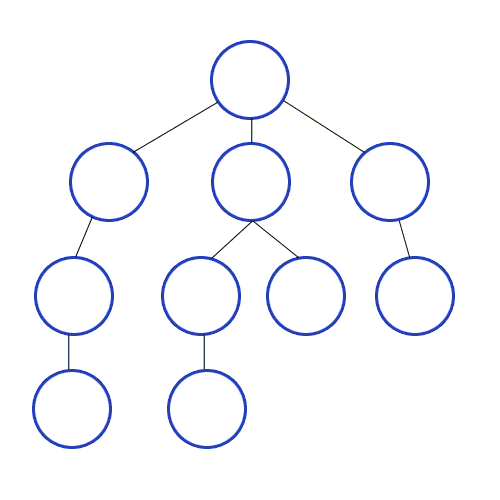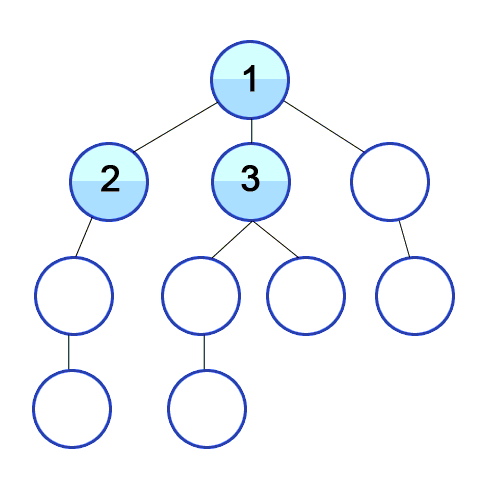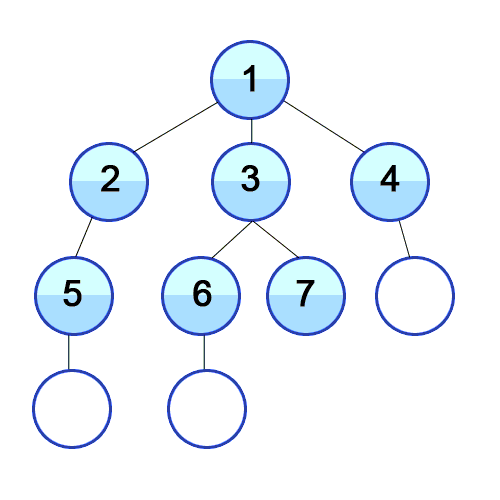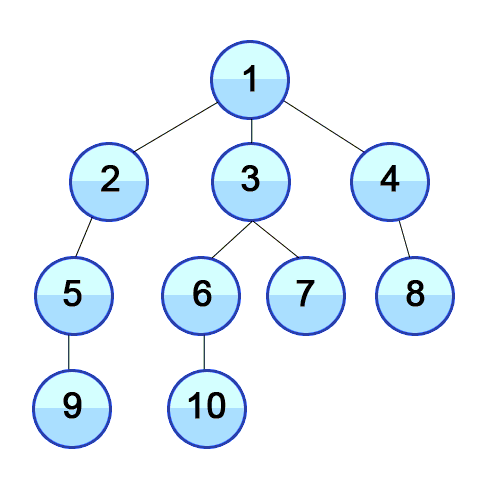
BFS 탐색 순서

1. 0번을 시작으로 좌/우측 자식 노드의 존재 여부를 확인
2. 좌측부터 1번 노드와 2번 노드를 순차적으로 방문
3. 1번 노드를 방문. 자식 노드인 3,4번 노드를 순차적으로 방문할 것을 기록
4. 2번 노드를 방문. 자식 노드인 5,6번 노드를 순차적으로 방문할 것을 기록
5. 3,4,5,6노드를 순차적으로 방문
6. 더 이상 방문해야 할 인접 노드가 없어질 때까지 위 과정 반복.

위 과정을 보면 다양한 경우를 순차적으로 방문하는 방식인 것을 알 수 있다. 즉, FIFO(First in First out)와 동일한 형태를 갖는다.

BFS 구현

위에 말한바와 연결되어 따라서 BFS는 Queue 또는 FIFO 방식의 자료구조를 사용하여 구현한다.
과정을 설명하면 아래와 같다.

1. 시작 노드(root)를 기준으로, 좌/우측 자식 노드(인접노드)를 확인
2. 좌/우측의 자식 노드가 존재하면 순차적으로 방문하기 위해 Queue에 저장
3. while 반복문을 사용하여 Queue에 저장된 인접 노드를 순차적으로 방문
4. Queue에 더이상 방문할 인접 노드가 없을 때까지 반복.

BFS 적용

BFS는 최단 거리/경로를 계산할 때 주로 사용한다.

BFS가 최단 거리/경로를 계산할 때 사용되는 이유는, 인접 노드를 우선적으로 탐색하기 때문이다.
DFS는 목적지와 반대 방향을 탐색해도 끝까지 탐색을 한다. 따라서 DFS는 최단 거리를 보장할 순 없다.

하지만 BFS는 인접 노드를 순차적으로 탐색한다.
즉, 목적지와 가까운 노드를 순차적으로 탐색한다. 따라서 BFS는 최단 거리를 확인하는데 유리한 알고리즘인 것이다.

시간 복잡도

• 인접 리스트 : O(V+E)
• 인접 행렬 : O(V^2)

DFS와 BFS

DFS와 BFS

DFS

• 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색
• Stack 혹은 재귀함수로 구현

BFS

• 현재 정점에 연결된 가까운 점들부터 탐색
• Queue를 이용해 구현

시간 복잡도

두 방식 모두 조건 내의 모든 노드를 검색한다는 점에서는 시간 복잡도는 동일하다.
BFS와 DFS 둘 다 다음 노드가 방문하였는지를 확인하는 시간과 각 노드를 방문하는 시간을 합하면 된다.

N이 노드, E가 간선일 때,

• 일접 리스트 : O(N+E)
• 인접 행렬 : O(N^2)

일반적으로 E의 크기가 N^2에 비해 상대적으로 적기 때문에, 인접 리스트 방식이 효율적이다.