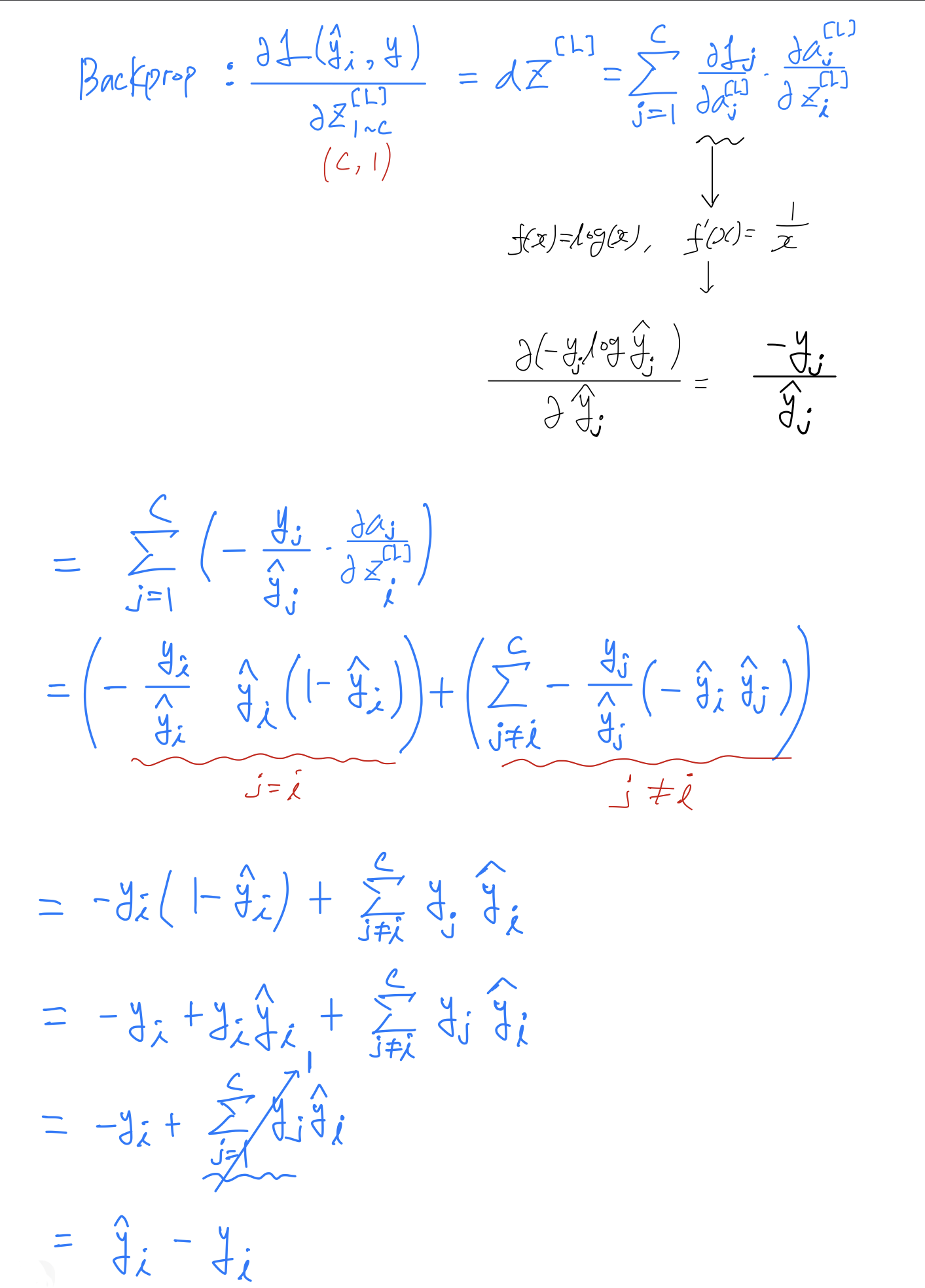Softmax Regression

• So far, the classification examples we've talked about have used binary calssification,
  where you had two possible labels, 0 or 1.
  What if we have multiple possible classes?
  There's a generalization of logistic regression called Softmax regression.

• Let's say that instead of just recognizing cats,
  you want to recognize cats, dogs, and baby chicks.
  So i'm going to call cat is class 1, dog is class 2, baby chick is class 3 and
  if none of the above, then i'm going to call class 0.
  i'm going to use capital $C$ to denote the number of classes you're trying to categorize your inputs.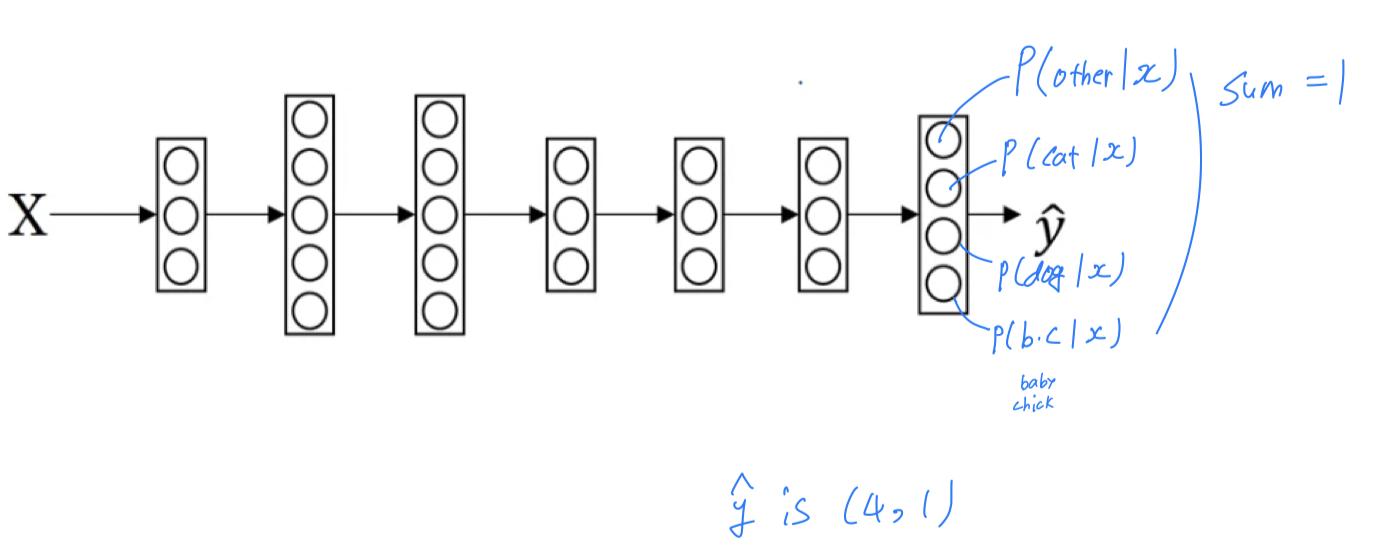And this cases, you have $4$ possible classes.
  So the number indexing your classes would be $0$ ~ $(C-1)$.
  In this case, we're going to build a new $X, Y$ where the output layer has $4$.
  In general $n^{[L]} = C$.
  And what we want is for the number of units in the output layer to tell us what is the probability of each of these $4$ classes.
  So here, the output layer $\hat{y}$ is oing to be a $(4, 1)$ dimensional vector,
  because it now has to output $4$ numbers, giving you these $4$ probabilities.
  And because probabilities should sum to $1$,
  the $4$ number in the ouput $\hat{y}$, they should sum to $1$.

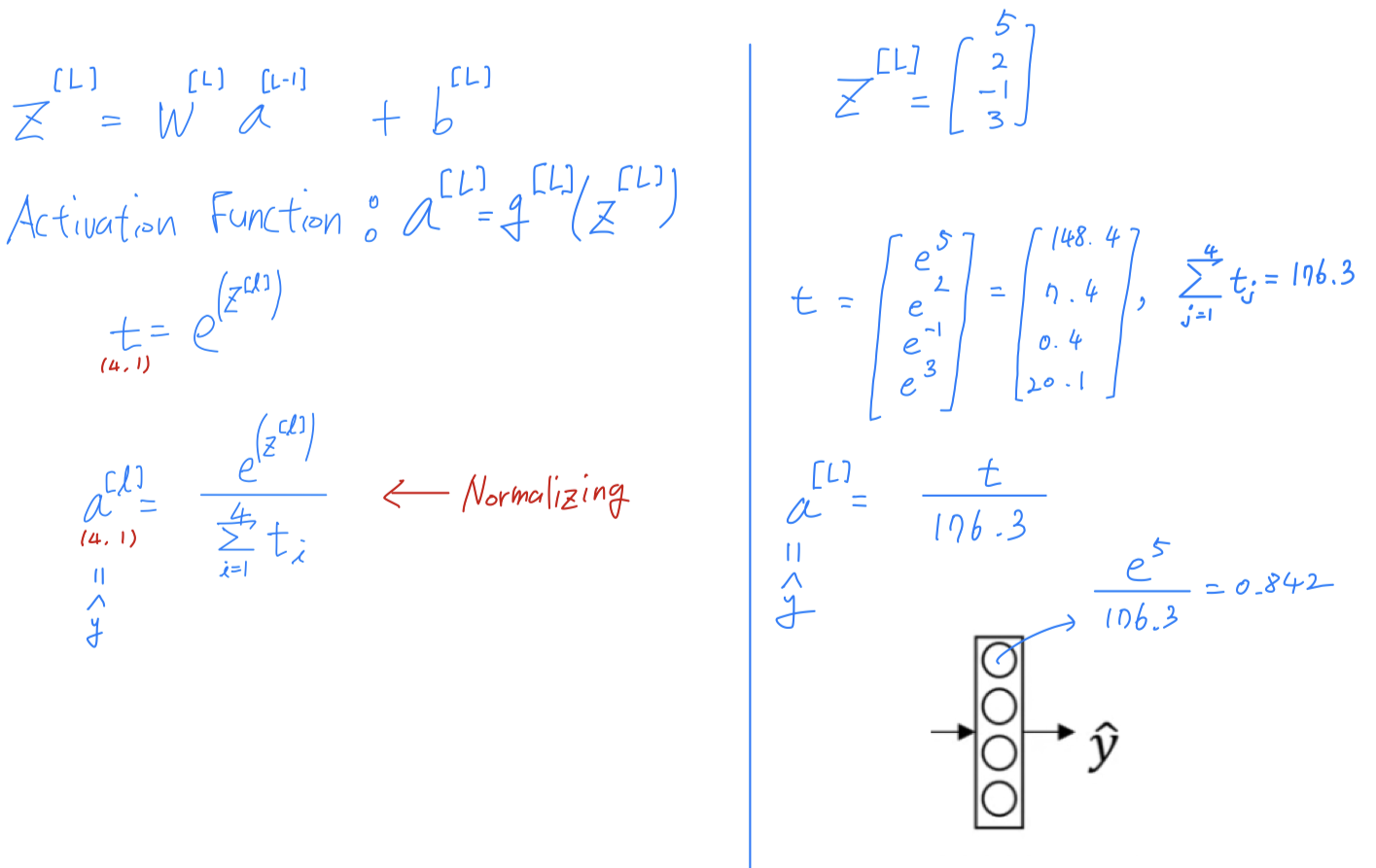
Softmax layer

• The standard model for your network to do this what's called a Softmax layer,
  and the ouput layer in order to generate these outputs.
  So that activation function is a bit unusual for the Softmax layer.
  

Softmax examples

• Here's one example with just raw inputs $x_1, x_2$.
  A softmax layer with $C=3$ output classes can represent this type of decision boundaries.
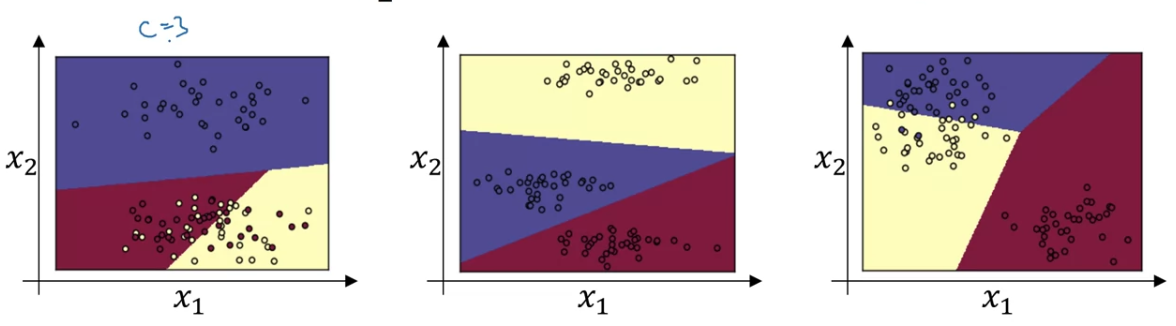  It's an example with $C=4$ and more than that.
  

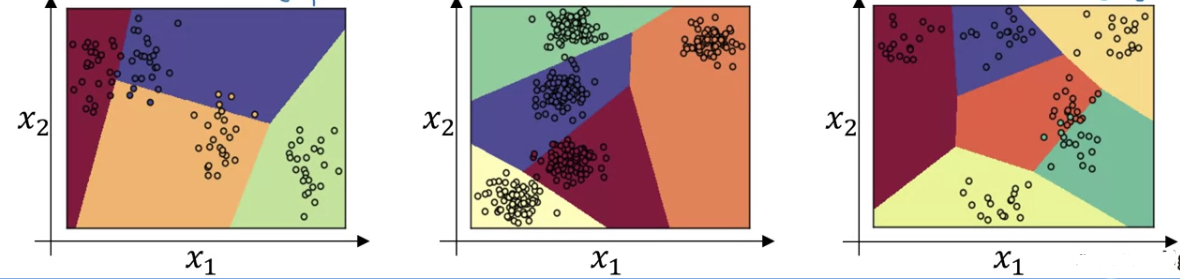
  So this is shows the tpye of things the Softmax classifier can do when there is no hidden layer of class,
  even much deeper neural network with $x$ and then some hidden units, and then more hidden units, and so on.
  Then you can learn even more complex non-linear decision boundaries to separate out multiple different classes.
  (hidden unit 개수, hidden layer 개수, 등 더 많아진 deeper neural network를 통해 훨씬 더 복잡한 nonlinear한 decision boundary를 학습하여 multiple class를 classification할 수 있다.)

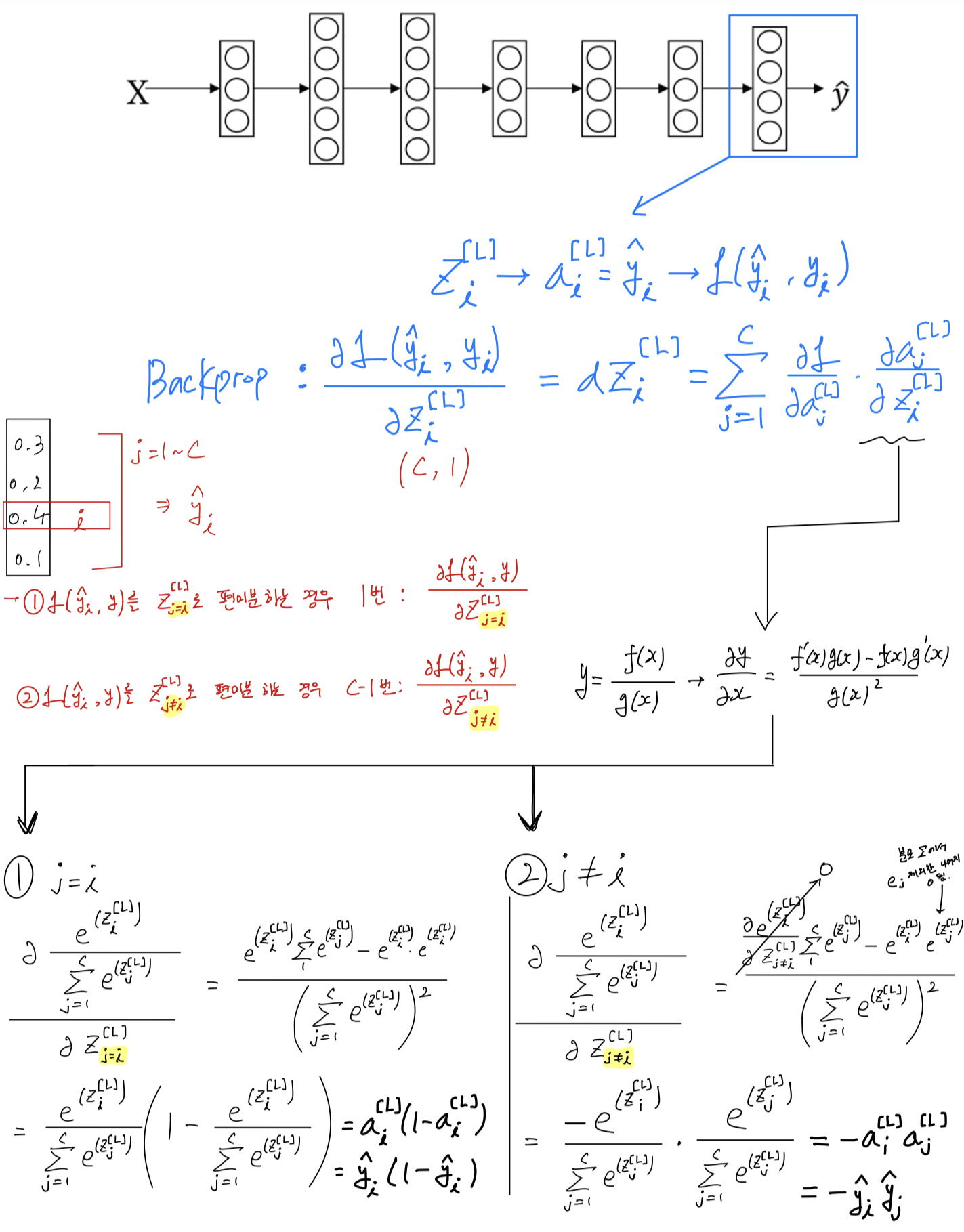
Training a Softmax Classifer

• You will learn how the training model that uses a softmax layer.
  Softmax is a generalization of logistic regression to more than two classes.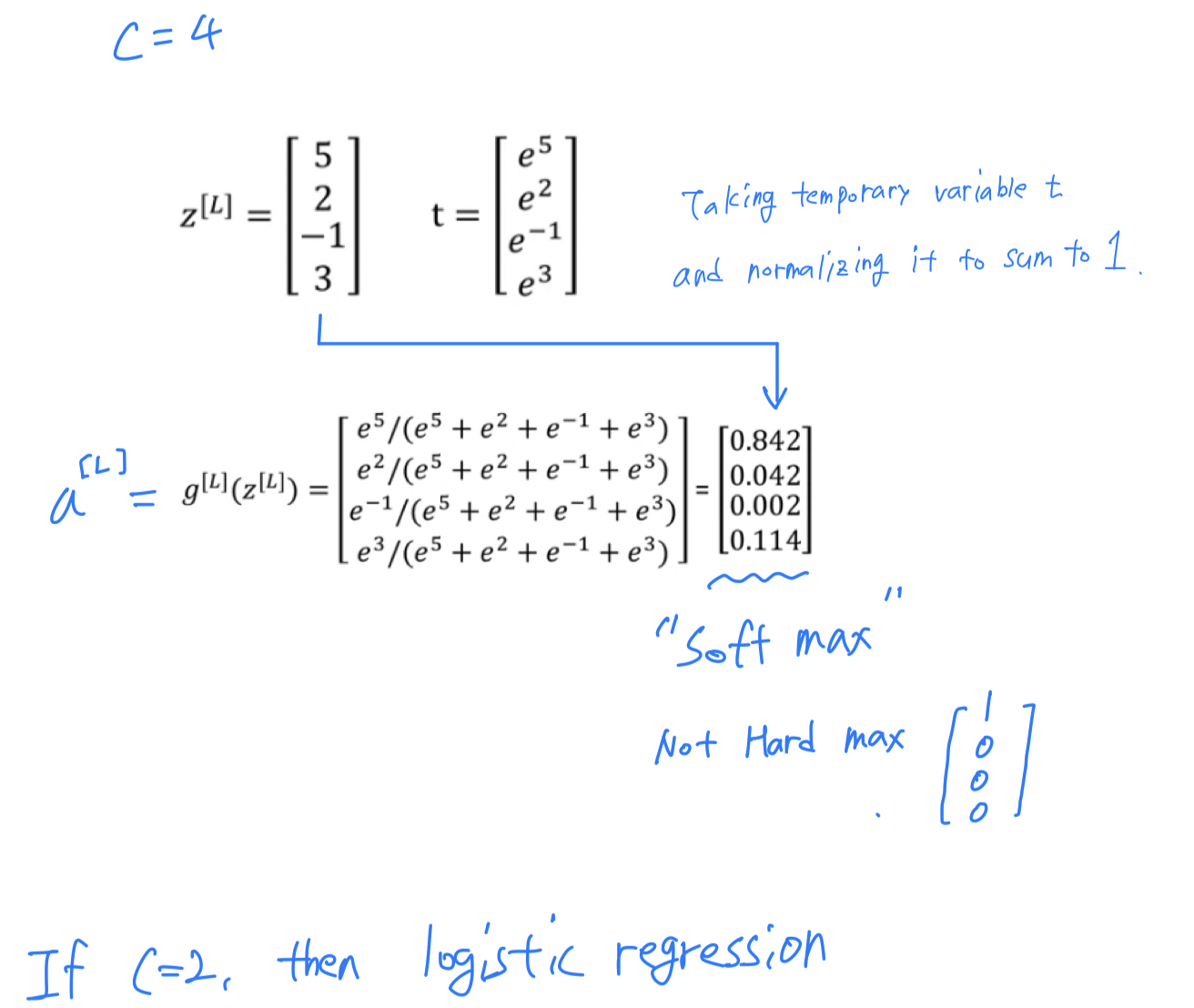

Loss function

• Let's define the loss functions you use to train your neural network.
  Loss is on a single training example.
  So more generally, what this loss function does is it looks at whatever is the ground truth class in your training set,
  and it tries to make the corrresponding probability of that class as high as possible.
  

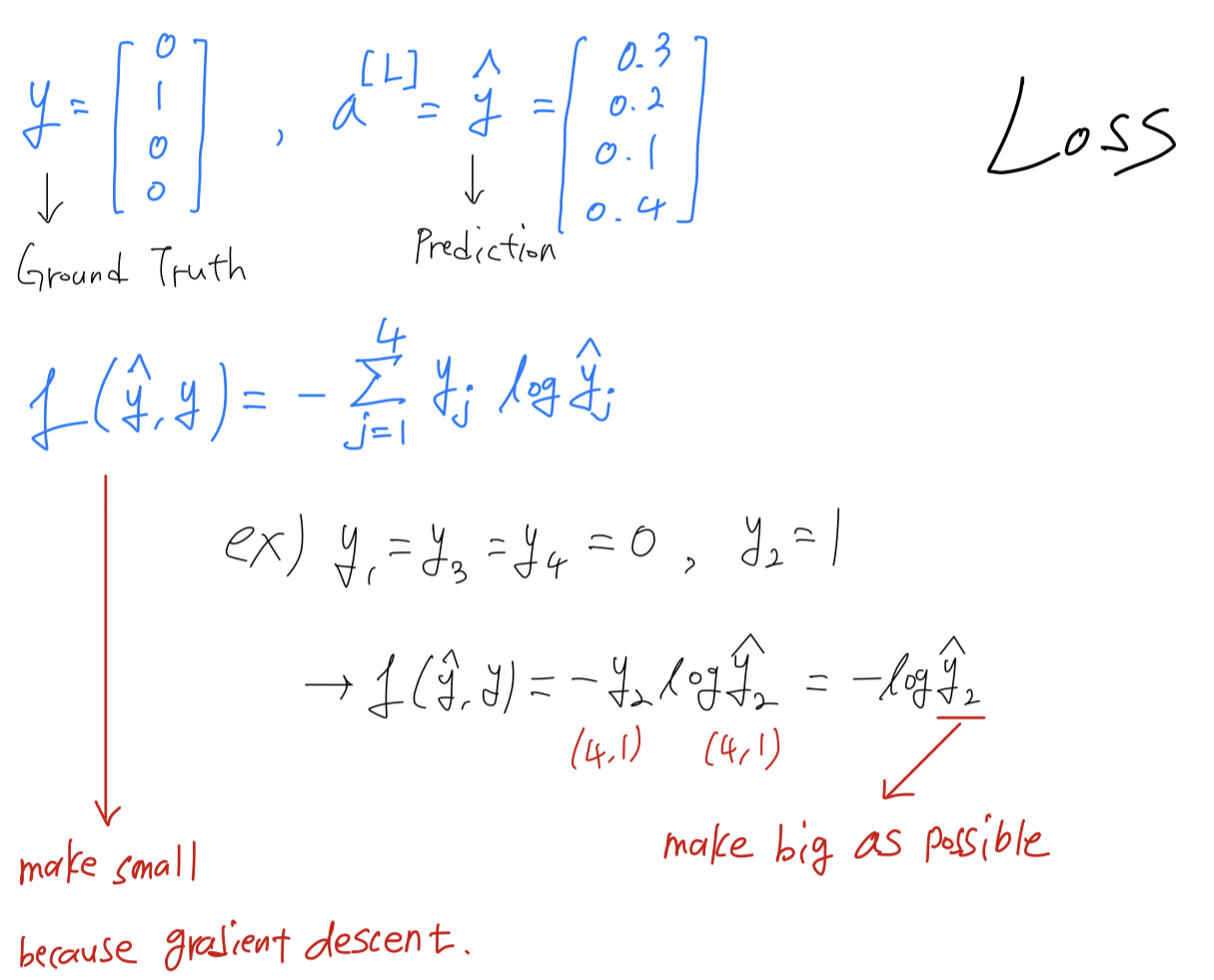
Cost function

• How about the cost $J$ on the entire training set.
  

Gradient descent with softmax

$dZ^{[L]} = \hat{Y} - Y$