서론

문제의 해결에 도움이 될 좌표계를 선정하는 것과 복잡한 함수를 단순한 형태의 함수로 근사하는 건 수학/과학/공학에서 흔하게 사용되는 방법이다. 이번 글에서는 레이 트레이싱을 구현할 때 사용할 수식의 유도에 필요한 구면 좌표계, 원통 좌표계 그리고 비선형 변환을 선형 변환으로 근사하여 성질을 분석하는 방법을 다룰 것이다.

본론

원기둥 좌표계

원기둥 좌표계는 원기둥을 표현하는 데 적합한 좌표계이다. 이 좌표계에서 3차원 공간의 좌표는 $(r, \phi, z)$로 표현된다. 하지만 이 시리즈에서는 일반적인 표기법을 따르지 않고 좌표를 $(r, \phi, y)$로 표현할 것이다. 그 이유는 일반적으로 위를 가리키는 축을 z축으로 사용하지만, 이 시리즈에서는 아래의 그림과 같이 위를 가리키는 축이 y축이기 때문이다.

$\phi$는 azimuth각을 나타내고 r은 y축으로부터의 거리 그리고 y는 직교 좌표계의 y와 동일하다. 원기둥 좌표계는 광선과 원기둥의 접점 그리고 원기둥의 법선 벡터를 계산할 때 사용될 수 있다. 이는 이후의 글에서 더 자세히 다룰 것이다.

원기둥 좌표계의 기저 벡터

원기둥 좌표계의 기저 벡터를 알아보기 전에 직교좌표계의 기저 벡터를 살펴보자. 직교좌표계의 표준 기저 벡터는 아래 세 성질을 갖는다.

1. 기저벡터는 성분이 증가하는 방향을 갖는다.
2. 기저벡터는 서로 직교한다.
3. 기저벡터는 단위벡터이다.

원기둥 좌표계에서 흔히 쓰이는 표준 기저 벡터 또한 위의 세 성질을 갖는다. 위의 세 성질을 충족하는 단위 벡터는 아래의 그림에 있는 기저 벡터밖에 존재하지 않는다.

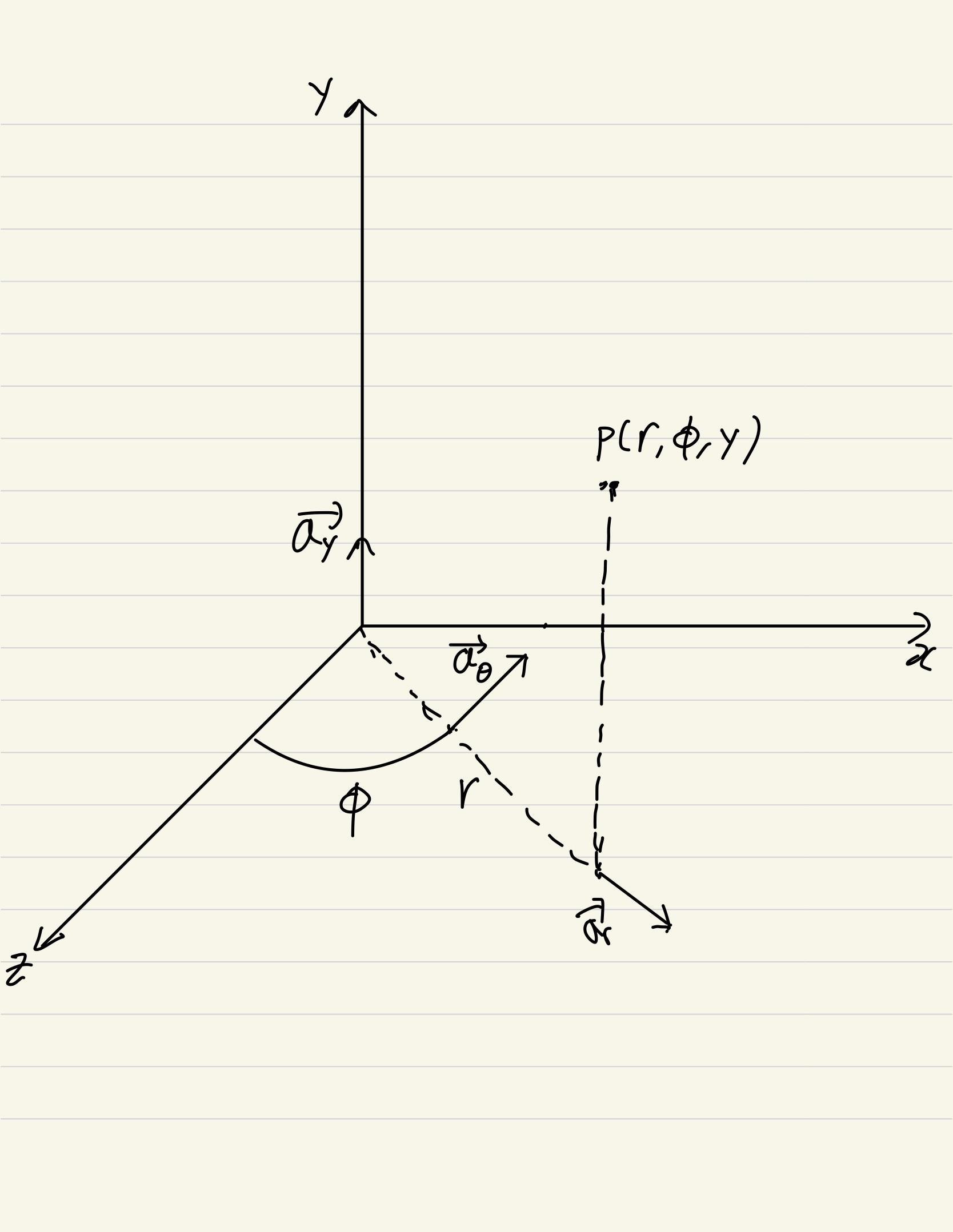
위의 그림에서 $\vec{a_r}$ $\vec{a_y}$ $\vec{a_\phi}$는 각각 $r$, $y$, $\phi$ 방향의 단위 기저벡터를 나타낸다. 여기에서 중요한 사실은 r 방향의 단위 벡터가 원기둥의 법선 벡터가 된다는 점이다.

원기둥 좌표계와 직교 좌표계의 기저 벡터 변환

기저 벡터 변환을 다루기 전에 벡터의 내적은 한 벡터를 다른 벡터에 투영한 것과 동일함을 기억하자. 그렇기에 기저 벡터의 변환은 내적을 통해 유도할 수 있다.

그 중에서 원기둥의 법선 벡터인 $\vec{a_r}$을 직교 좌표계의 기저 벡터의 성분으로 아래와 같이 변환할 수 있다.

$\vec{a_r} \cdot \vec{a_x} = cos(\frac{\pi}{2} - \phi) = sin(\phi)$ (eq.0)
$\vec{a_r} \cdot \vec{a_y} = cos(\frac{\pi}{2}) = 0$ (eq.1)
$\vec{a_r} \cdot \vec{a_z} = cos(\phi)$ (eq.2)

구면 좌표계

구면 좌표계에서 3차원 공간의 좌표는 $(\phi, \theta, \rho)$로 표현된다. 원기둥 좌표계의 표준 기저 벡터도 구면 좌표계의 표준 기저 벡터를 구한 방법을 동일하게 사용하여 구할 수 있다.

필자가 구면 좌표계를 사용한 것은 빛과 관련된 물리량 간에 관계를 수식으로 나타낼 때 구면 좌표계를 사용하면 편하기 때문이다. 구체적으로는 구면 좌표계에서 구의 면적 적분과 체적 적분은 무척 단순하다. 우선 직교 좌표계에서의 체적 적분을 살펴보자.

직교좌표계 구 적분

직교 좌표계에서 구의 체적 적분은 아래의 형태를 띤다.

$\int_{z_0}^{z_1}\int_{y_0}^{y_1}\int_{0}^{1}f(x,y,z)dxdydz$ (eq.3)
$=\int_{x_0\prime}^{x_1\prime}\int_{y_0\prime}^{y_1\prime}\int_{0}^{1}{f(x,y,z)dzdydx}$ (eq.4)

위의 두 식은 동일하게 구의 체적 적분을 나타낸 것인데 적분의 순서가 다르다. 적분의 순서가 달라지면서 아래와 같이 변수별 적분의 범위가 달라진다.
$y_0 \neq y_0\prime$
$y_1 \neq y_1\prime$
$x_0 \neq x_0\prime$
$x_1 \neq x_1\prime$

적분의 순서를 바꿨을 때, 적분의 범위가 달라지는 것은 x, y, z의 값이 서로 독립적이지 않기에 생기는 일이다. x와 y의 값이 무엇이냐에 따라서 z의 값이 정해진다. y와 z의 값에 따라서도 x의 값이 정해지고 x와 z의 값에 따라서 y의 값이 정해진다.

구면좌표계 구 적분

구면 좌표계에서 구의 체적 적분은 아래의 형태를 띤다.

$\int_{\phi_0}^{\phi_1}\int_{\theta_0}^{\theta_1}\int_{\rho_0}^{\rho_1}{Cf(\rho, \theta, \phi)d\rho d\theta d\phi} = \int_{\theta_0}^{\theta_1}\int_{\phi_0}^{\phi_1}\int_{\rho_0}^{\rho_1}Cf(\rho, \theta, \phi)d\rho d\phi d\theta$ (eq.5)

위에서 보다시피 적분의 순서를 바꾸어도 범위는 바뀌지 않는다. $\rho$ $\phi$ $\theta$의 값이 서로 독립적이기 때문에 적분의 순서를 손쉽게 바꿀 수 있다.

$C$의 정체

(eq.5)에는 (eq.3)와 (eq.4)에서 볼 수 없었던 수 $C$가 있음을 확인할 수 있다. 이는 구면 좌표계에서의 적분 결과를 표준 기저 벡터로 구성된 직교좌표계에서의 적분 결과로 바꾸는 역할을 한다. $C$를 유도하기 위해서는 자코비안 행렬과 행렬식에 대해 알고 있어야 한다.

우선 직교 좌표계에서 구면 좌표계로의 변환은 비선형적이다. 모든 행렬은 선형 변환이기 때문에 비선형 변환인 $구면 좌표계 -> 직교 좌표계$로의 변환을 행렬로 표현할 수 없다. 하지만 로컬한 레벨에서 비선형 변환을 선형 변환으로 근사할 수 있다. 이렇게 근사하여 행렬로 표현한 것이 자코비안 행렬이다. 왜 자코비안 행렬로 표현할까? 행렬을 좌표계의 변환으로 볼 수 있음을 기억하자. 어떤 좌표계 변환을 표현한 행렬의 행렬식은 해당 좌표계 변환이 불러오는 크기의 변화를 나타낸다. 그렇기에, 구면 좌표계를 선형 근사한 자코비안 행렬의 행렬식은, 구면 좌표계에서의 공간의 크기가 직교 좌표계에서 어떻게 변화하는지 나타내는 것이다. $C$는 이런 자코비안 행렬의 행렬식이 된다. 자세한 내용은 텍사스 대학교 오스틴 캠퍼스의 https://web.ma.utexas.edu/users/m408m/Display15-10-8.shtml 를 참고하자.