레이 트레이싱 구현기
1.레이 트레이싱 구현기 0. 왜 레이트레이싱을 공부했나?

다양한 온라인 컴퓨터 게임을 하며 자란 한국인에게, 컴퓨터 그래픽스는 누구나 한 번쯤 공부해 보고 싶은 분야일 것이다. 하지만, 아주 단순한 그래픽을 구현하는 것조차도 필요한 수식을 유도하면서 진행하고자 한다면, 생각보다 많은 선행 지식(선형대수학, 사영기하, 기하광학
2.레이 트레이싱 구현기 1-1 배경 지식: 선형대수

선형대수학은 공학을 공부해본 학생이라면 누구나 한 번쯤 수강했거나 앞으로 수강해야할 과목이다. 대부분의 학생이 수강하는만큼 선형대수는 다양한 분야에서 활용되는데, 3d 그래픽도 예외는 아니다. 선형대수학은 아직도 연구가 진행되는 분야이고 인류는 행렬에 대해 많은 지식을
3.레이 트레이싱 구현기 1-2 배경 지식: 좌표계와 선형 근사
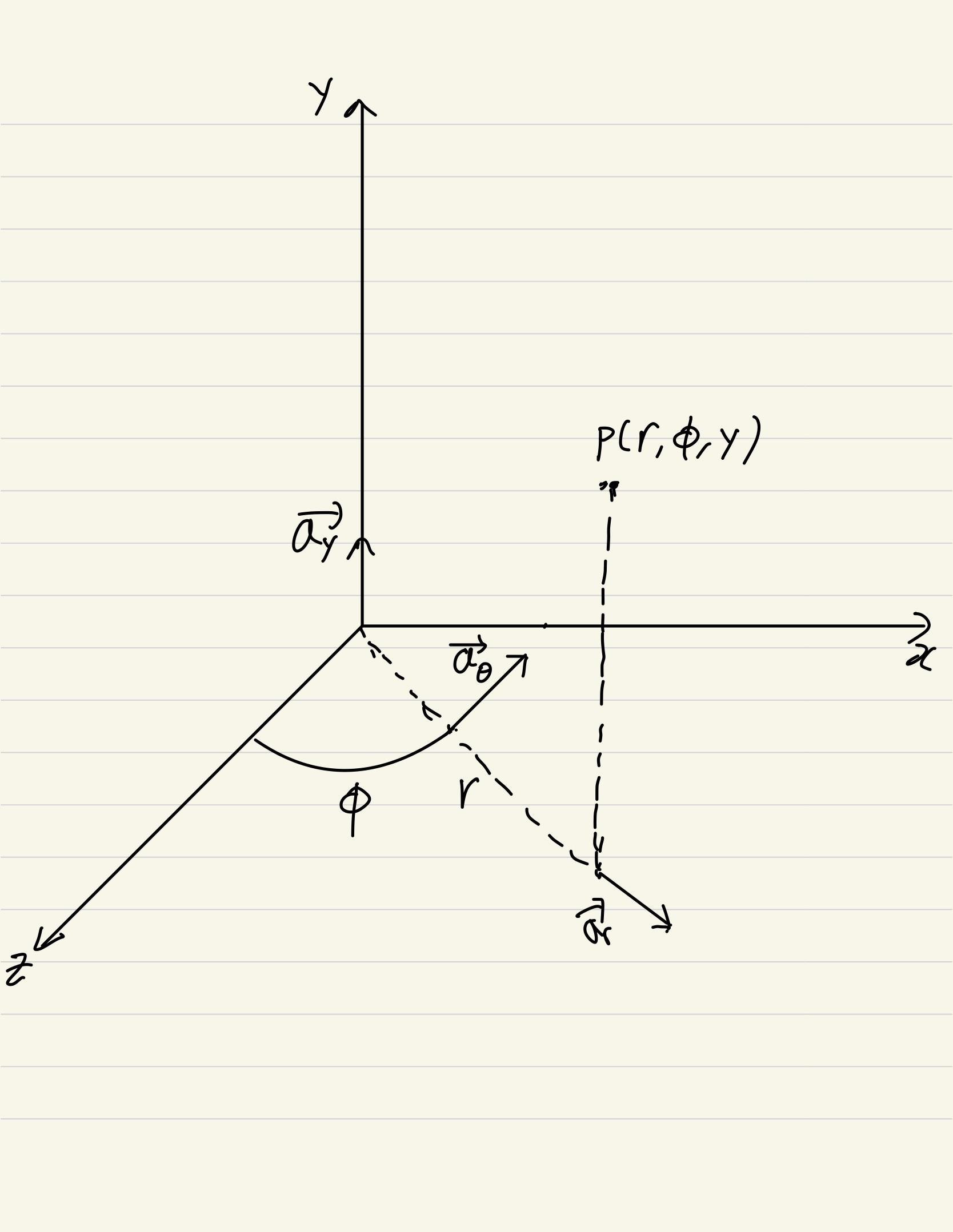
서론 사실 수식을 유도/이해하지않고 단순히 레이트레이싱을 구현하는 것이 목표라면, 다양한 선형 좌표계와 비선형 좌표계를 알아야하는건 아니다. 하지만 단순히 수식을 받아들이는 건 재미없고 따분한 일이다. 이번 글에서는 수식 유도에 필요한 구면 좌표계, 원통 좌표계 그리
4.레이 트레이싱 구현기 1-3 배경 지식: radiometry

레이 트레이싱은 광선을 추적해서 이미지를 렌더링한다. 레이 트레이싱은 빛을 다루기 때문에, 빛의 측정에 대해 알면 수식을 유도하는데 큰 도움이 된다. 빛의 측정을 다루는 학문인 radiometry에 대해 간략하게 살펴보자.하나의 광자가 갖는 에너지는 아래와 같다.$Q
5.레이 트레이싱 구현기 2-1. Pinhole Camera
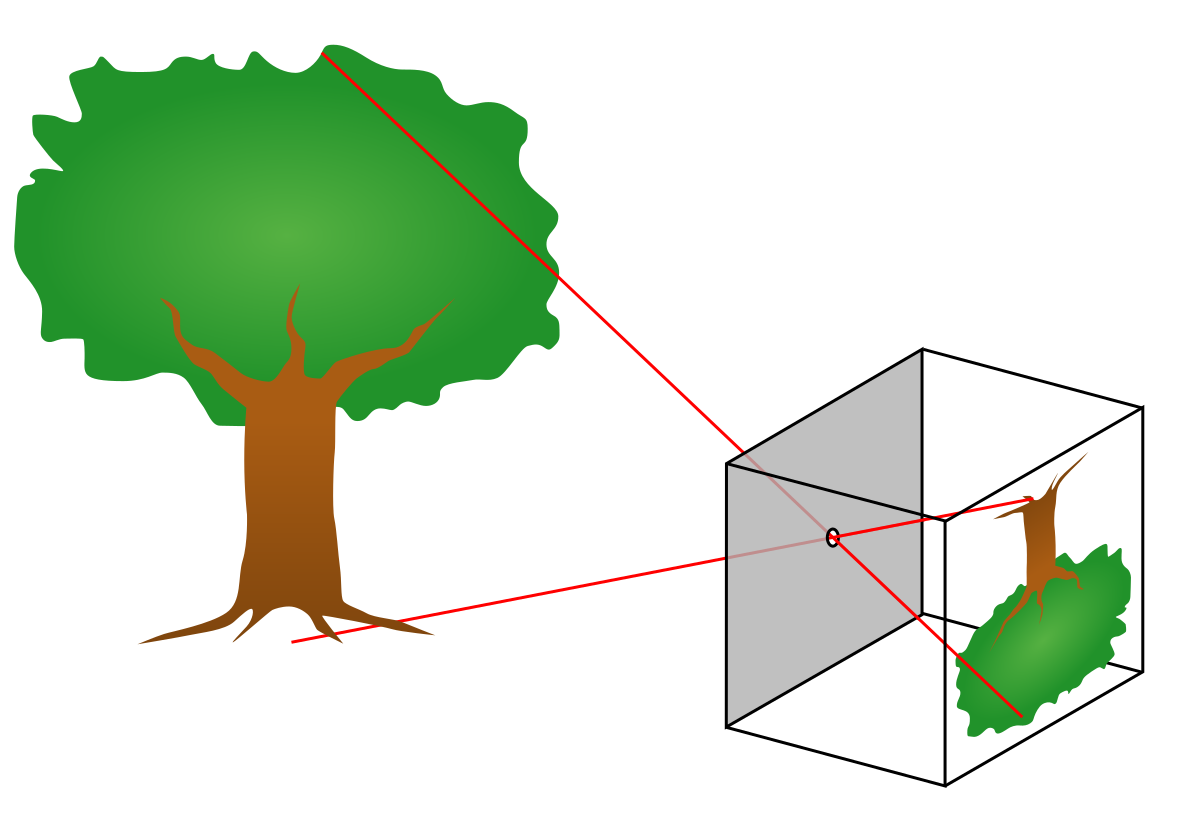
우리가 사는 공간은 삼차원적이다. 필자가 지금 타이핑하고 있는 키보드의 위치는 세 개의 실수로 표현될 수 있을 것이다. 이처럼 많은 사람이 물리적 공간을 3차원 실공간으로 모델링한다. 우리가 원하는 것은, 삼차원 실공간에 존재하는 대상을 모니터에 출력할 수 있는 형태로
6.레이 트레이싱 구현기 2-2. Pinhole Camera의 구조, 원리 그리고 구현
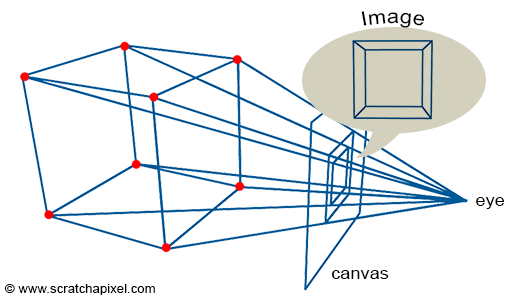
저번 글을 통해, 핀홀 카메라의 구조와 원리 그리고 구현해야할 내용에 대해 살펴봤다. 이제 삼차원 실공간에 존재하는 대상을 이차원 평면에 대응시켜줄 가상 카메라에 대해 더 살펴본 뒤 레이트레이싱의 종류를 알아보자.가상 카메라의 구조와 원리는 아래와 같다.출처: scra
7.레이 트레이싱 구현기 2-3. 광선과 좌표계

시리즈의 이전 글에서 3차원 실공간을 2차원 평면인 캔버스에 맵핑하는 방법을 다뤘다. 이번 글에서는, 캔버스에 맵핑된 점과 카메라를 지나는 광선을 카메라 로컬 좌표계에서 생성하고 이를 글로벌 좌표계로 변환하는 과정을 다룰 것이다.저번 글에서 계산을 단순화하기 위해서 캔
8.레이 트레이싱 구현기 3-1 Visibility와 Shading 문제란?

시리즈의 이전 글을 통해 레이 트레이싱을 구현하기 위해 필요한 수학적 배경 지식을 습득하고 카메라를 구현해봤다. 이제 렌더링을 크게 visibility와 shading으로 나누어서 각 파트가 어떤 기능을 수행해야할지 알아보자.필자의 앞에 커다란 벽이 있고 벽 뒤에 어떤
9.레이 트레이싱 구현기 3-2 법선 벡터와 교점: 원기둥

이전 글에서 visibility와 shading 문제가 무엇인지 알아봤다. 이것을 해결하기 위해서는 광선과 물체들간에 교점을 구하고 물체의 법선 벡터를 구할 수 있어야한다. 필자는 구, 원기둥 그리고 평면을 렌더링했는데 이 세 도형의 법선 벡터와 교점을 구하는 방법을
10.레이 트레이싱 구현기 3-3 난반사 표면 렌더링

이전 글에서 원기둥과 광선의 접점 그리고 원기둥의 법선 벡터를 구하는 방법을 알아봤다. 이번 글에서는, 접점과 법선 벡터를 사용하여 난반사 표면을 렌더링하는 방법을 배워보자. 난반사 표면이란? 정반사 표면에서 표면에 들어오는 광선과 법선 벡터는 입사각을 이루고 반사