Intuition 1 && Approach 1

subarray 형태를 찾아야하니 누적합을 활용하면 좋을 것 같다는 생각이 들었다.

int maxSubArray(int* nums, int numsSize){
    int prefix[numsSize];
    prefix[0]=nums[0];
    for (int i=1;i<numsSize;i++){
        prefix[i]=prefix[i-1]+nums[i];
    }

    int max=nums[0];
    for (int i=0;i<numsSize;i++){
        if (prefix[i]>max) max=prefix[i];
        for (int j=i+1;j<numsSize;j++){
            if (prefix[j]-prefix[i]>max) max=prefix[j]-prefix[i];
        }
    }
    return max;
}

누적합 배열을 만들면 $a_n$부터 $a_{n+k}$까지의 합은 $pre_{n+k}-pre_{n-1}$으로 $O(1)$에 구할 수 있다.

예를 들어, 아래와 같은 배열이 있을 때

누적합은 아래와 같이 작성되고

원래 배열의 1번(9) 인덱스부터 4번(2) 인덱스까지의 합을 원한다면 4번 인덱스까지의 누적합(12)에서 1번 직전 인덱스인 0번(5)의 누적합을 빼주면 되는 것이다.

그러나 이 방법은 코드를 작성하고나니 결국에 누적합에서 모든 경우의 수를 보기 위해 $O(n^2)$의 시간복잡도가 발생했고, 배열 최대 길이가 $10^5$인 문제 특성상 시간초과가 발생함이 자명했다.

Inutuition 2

다르게 접근하여, 배열길이 별로 케이스를 나눠 그때그때의 합을 구해보면 어떨까...
예를 들어,
배열 길이가 1인 케이스) 5/9/-1/-3/2
배열 길이가 2인 케이스) 5,9/9,-1/-1,-3/-3,2
.
.
.
그러나 조금만 생각해봐도 이또한 모든 경우의 수를 확인해야해서 $O(n^2)$이 발생한다.
정확하게는 n개의 요소를 가진 배열에서 연속된 k개의 요소를 뽑는 경우의 수를 생각해보면 된다.
시작 지점만 정해주면 하나의 경우의 수로 확정이 되므로 이 경우의 수를 계산하려면 시작 지점이 될 수 있는 경우의 수를 계산해주면 된다. 따라서 $n-k+1$이 각각의 k에 대해 발생한다.
$\displaystyle\sum_{k=1}^{n}(n-k+1)=n(n+1)-\displaystyle\sum_{k=1}^{n}k=O(n^2)$이 된다.

모든 경우의 수를 보는 것이 아니라 효율적으로 탐색하는 방법이 필요하다...

교수님 풀이

이건 이 문제에 적절한 풀이는 아니지만 누적합 없이도 Intuition&&Approach1과 같이 탐색을 하는 풀이라서 가져와봤다.
$\\$
$\\$
이 문제를 올바르게 풀기 위해서는 합이 최대가 되도록 해줘야한다는 점에 주목해야한다.
합이 양수면 그대로 안고가고 음수일때만 버려주면 된다. 최대한 큰 값을 만들어야 하기 때문에 일단 현재합이 양수면 이 다음에 양수가 올때, 버릴 때보다 값이 커지기 때문이다.
그리고 이 합들을 저장해놓고 나중에 최댓값을 찾아주면 된다.

예를 들어 아래와 같은 배열이 있다고 해보자.

그 다음 1번 인덱스는 9이므로 선택하는 것이 이득이다.
(합의 배열 : $[9,0,0,0,0]$)

그 다음 -2는 음수니까 버리는 것이 이득이라고 잘못생각할 수도 있지만, 앞서 언급했듯이 일단 합이 양수가 되면 이 다음에 양수가 올 때 그 합이 더 커지게 해줄 것이다.
(합의 배열 : $[9,7,0,0,0]$)

5는 양수이므로 합이 더 커지게 해줄 것이다.
(합의 배열 : $[9,7,12,0,0]$)

-15는 합산 결과가 음수이므로 이 다음에 무엇이 오든간에 합을 작게 만들어 줄것이므로 버린다.
이때 버리는 행위는 이 다음 합의 배열을 이전처럼 직전 합의 배열에서 합산하는 것이 아니라, 0부터 다시 시작함으로써 이루어진다.
(합의 배열 : $[9,7,12,-3,0]$)

10은 양수이므로 합이 더 커지게 해줄 것이다.
(합의 배열 : $[9,7,12,-3,10]$)

그리고 이 합의 배열에서 가장 큰 값인 12를 찾아주면 문제는 해결된다.그런데 여기에서 조금 더 생각해보면, 그때그때 합이 max값보다 큰지 비교하면 굳이 추가적인 메모리 사용없이도 문제를 해결할 수 있다. 아래가 여기까지 적용된 교수님의 코드와 내가 작성한 코드다.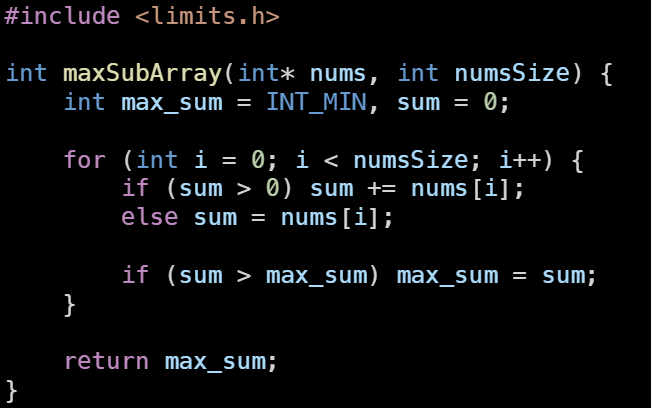

int maxSubArray(int* nums, int numsSize){
    int sum=0, max=nums[0];

    for (int i=0;i<numsSize;i++){
        sum+=nums[i];
        if (sum>max){
            max=sum;
        }
        if (sum<0){
            sum=0;
        }
    }

    return max;
}

+) 만약에 문제가 변형되서 양수음수가 섞인 요소들간에 최대 곱을 구하라한다면, 원래 숫자에 $log$를 취해서 합으로 만들어서 문제를 해결할 수 있다.

Complexity

• Time Complexity : $O(n)$
• Space Complexity : nums배열을 담을 공간이 필요하다. $O(n)$

지적 및 질문 환영합니다.