Intuition

배열의 길이가 50000개로 제한되어있기 때문에 지금까지 배열에 등장한 숫자를 저장해서 그게 몇 개 나왔는지 체크하는 것이 가능할 것이라고 생각했다.

Approach

어떤 숫자가 몇개 나왔는지 저장하기 위해서 구조체를 만들었다. num은 배열의 첫번째 원소로(문제의 숫자 범위가 광범위해서), 수량은 0으로 초기화를 시켰다.

typedef struct Arr_{
    int num;
    int quantity;
}Arr;

Arr arr[50000];
    for (int i=0;i<50000;i++){
        arr[i].num=nums[0];
        arr[i].quantity=0;
    }

배열을 순회하면서 숫자가 나올 때마다 해당 숫자가 arr배열에 존재하는지 체크하고, 만약 존재한다면 수량을 올려주고, 존재하지 않는다면 arr배열에 새롭게 저장해주었다. 이때, arrIdx변수를 사용해 새롭게 저장할 인덱스를 컨트롤 해주었다.
그리고 이 과정에서 max값을 찾는 작업도 동시에 진행해주었다.

int find=finder(arr,nums[i]);
if (find>=0){
	arr[find].quantity++;
    if (arr[find].quantity>max.quantity){
    	max.num=arr[find].num;
    	max.quantity=arr[find].quantity;
    }
}
else{
	arr[++arrIdx].num=nums[i];
    arr[arrIdx].quantity++;
    if (arr[arrIdx].quantity>max.quantity){
    	max.num=arr[arrIdx].num;
        max.quantity=arr[arrIdx].quantity;
    }
}

int finder(Arr* arr,int target){
    for(int i=1;i<50000;i++){
        if (arr[i].num==target){
            return i;
        }
    }
    return -1;
}

그런데 이때 주의해야할 것이, 내가 초기화를 배열의 첫번째 원소로 해주었기 때문에 배열의 첫번째 원소와 같은 숫자가 등장할 때에는 finder함수에서 처리할 것이 아니라 따로 처리시켜줘야한다.

if (nums[0]==nums[i]){
            arr[0].quantity++;
            if (arr[0].quantity>max.quantity){
                max.num=arr[0].num;
                max.quantity=arr[0].quantity;
            }
        }

Solution

typedef struct Arr_{
    int num;
    int quantity;
}Arr;

int majorityElement(int* nums, int numsSize){
    Arr arr[50000];
    for (int i=0;i<50000;i++){
        arr[i].num=nums[0];
        arr[i].quantity=0;
    }

    int arrIdx=0;
    Arr max;
    max.quantity=0;

    for (int i=0;i<numsSize;i++){
        if (nums[0]==nums[i]){
            arr[0].quantity++;
            if (arr[0].quantity>max.quantity){
                max.num=arr[0].num;
                max.quantity=arr[0].quantity;
            }
        }
        else{
            int find=finder(arr,nums[i]);
            if (find>=0){
                arr[find].quantity++;
                if (arr[find].quantity>max.quantity){
                    max.num=arr[find].num;
                    max.quantity=arr[find].quantity;
                }
            }
            else{
                arr[++arrIdx].num=nums[i];
                arr[arrIdx].quantity++;
                if (arr[arrIdx].quantity>max.quantity){
                    max.num=arr[arrIdx].num;
                    max.quantity=arr[arrIdx].quantity;
                }
            }
        }
    }

    return max.num;
}

int finder(Arr* arr,int target){
    for(int i=1;i<50000;i++){
        if (arr[i].num==target){
            return i;
        }
    }
    return -1;
}

complexity

• Time Complexity : for문안에서 매번 finder함수가 돌아간다. $O(n^2)$
• Space Complexity : 구조체 배열 만큼이 필요하다. $O(n)$

교수님 풀이 1

위에서 내가 한 방식과 동일하지만 훨씬 잘 짜여진 코드라고 생각한다. 내 코드와 비교해봤을 때 중요한 부분이 두가지 보였다.

첫번째, 나는 매번 finder함수에서 배열 전체를 돌게 만들었다. 그러나 arrIdx로 범위를 한정지어줬다면 훨씬 효율적이었을 것이다.

두번째, 나는 구조체를 만들어서 두배의 메모리 공간을 사용했다. 그러나 checked 배열을 해당 숫자가 등장했는지 여부를 확인하기위한 용도로만 사용하고, checked 배열에 없는 숫자가 나오면 그자리에서 바로 그 숫자가 nums배열에 몇개 있는지 확인 및 과반수 여부를 확인한다면 그럴 필요가 없다.

complexity

• Time Complexity : 배열에 같은 숫자가 단 두개고 나머지가 모두 각각 다른 숫자일때가 worst case가 될 것이다. $O(n^2)$
• Space Complexity : checked만큼이 필요하다. $O(n)$

교수님 풀이 2

사실 이 포스팅의 메인부분이다.

이 문제는 appearing more than ⌊n / 2⌋ times인 하나의 숫자를 찾는 문제이다. (절반 초과인 수를 찾는 문제다. 딱 절반은 안된다.) 이 문제를 푸는 유명한 알고리즘이 Boyer-Moore Voting Algorithm이다.

이 알고리즘은 서로 다른 두 개의 요소를 배열에서 배제시켜도 이전에 과반수였던 Majority Element는 이후에도 여전히 과반수라는 아이디어에서 출발한다.

예를 들어, A팀 5명과 B팀 15명이 절벽앞에 무작위로 섞여서 모여있다. 여기서 무작위로 두 명을 앞으로 불러내고 두명이 만약 서로 다른 팀이라면 둘다 절벽 아래로 떨어지고, 같은 팀이라면 다시 무리 속으로 들어간다. 그리고 이 일련의 과정은 두 팀 중 한팀만 남을때까지 계속된다.
극악의 확률로 같은팀 두명이 계속 뽑히지 않는 이상 언젠가 이 게임은 B팀의 승리로 끝나게 된다.

이제 아래 배열에 응용시켜보자. 배열을 순차적으로 순회하면서 Majority Element의 후보를 정해줄 것이고, Majority Element후보가 몇 번 등장했는지가 목숨 개수가 될 것이다. 목숨개수를 체크하며 0이 될때마다 교체해줄 것이다. 목숨은 1부터 시작한다.

#0) 우리는 0번 인덱스 0 하나만을 확인했다. 그러므로 일단 ME(Majority Element)는 0이고 목숨은 1이다.
#1) 3이 등장했다. 기존 ME인 0과 다르므로 ME는 3으로 교체되고 목숨은 1이다.
#2) 기존 ME와 동일하므로 ME는 3으로 유지되고 목숨은 2다.
#3) 기존 ME와 다른 0이 등장했다. 여전히 ME는 3이다. 그러나, 목숨은 1로 차감되었다.
#4) ME 3의 목숨이 0으로 차감되어 새로운 ME는 0이 되고 새롭게 목숨이 1로 설정된다.
#5) ME의 목숨이 2가 된다.
#6) ME의 목숨이 1이 되고, 결국 마지막에 남은 ME는 0이다.
$\\$
$\\$
아래는 목숨을 예시로 설명하는 것에 대한 이해를 도울 수 있는 그래프이다. x축이 등장하는 원소이고, y축이 목숨이다.

David Eppstein, CC0, via Wikimedia Commons

각각 이를 바탕으로 내가 작성한 코드와, 교수님의 코드이다.

int majorityElement(int* nums, int numsSize){
    int major=nums[0], majorCnt=1;
    for (int i=1;i<numsSize;i++){
        if (major==nums[i]){
            majorCnt++;
        }
        else{
            majorCnt--;
            if (majorCnt==0){
                major=nums[i];
                majorCnt++;
            }
        }
    }
    return major;
}

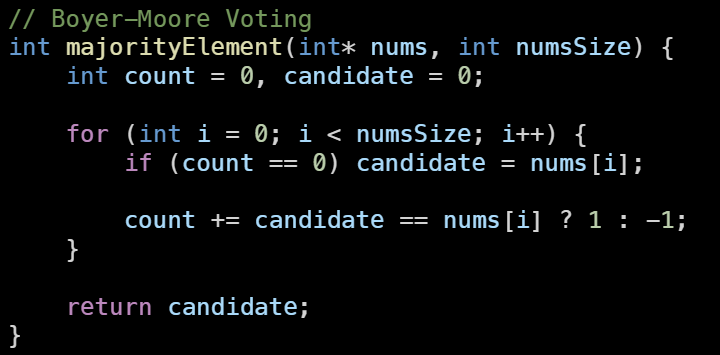반복문의 첫 시작을 목숨이 0인지 체크하여 ME를 교체하는 작업부터 시작하신다. 이렇게 하면 나처럼 배열의 첫 원소로 초기화시킬 필요가 없고 코드도 조금 더 깔끔해지는 것 같다.

Complexity

• Time Complexity : 배열을 한 번 순회한다. $O(n)$
• Space Complexity : nums배열 만큼이 필요하다. $O(n)$

$\\$
+) 이 문제는 the majority element always exists라고 제한시켜주었기 때문에 여기서 끝내도 된다. 그러나 일반적인 경우라면 이렇게 끝내선 안된다. 위와 같은 코드는 $[1,1,2,2],\,[1,2,3]$과 같이 과반수가 없는 경우에도 각각 2, 3을 반환하기 때문이다.
따라서, 아래와 같이 마지막에 남은 ME가 진짜 ME인지 체크하는 과정이 필요하다.

int majorityElement(int* nums, int numsSize){
    int major=0, majorCnt=0;
    for (int i=0;i<numsSize;i++){
    	if (majorCnt==0) major=nums[i];
        if (major==nums[i]) majorCnt++;
        else majorCnt--;
    }
    
    /* major인지 체크 */
    int cnt=0;
    for (int i=0;i<numsSize;i++){
    	if (major==nums[i]) cnt++;
    }
    if (cnt>numsSize/2) return major;
    else reuturn -1;
}

지적 및 질문 환영합니다.