Intuition

숫자 개수만큼 배열을 만들어 놓고 해당 숫자가 등장할때마다 배열을 +1하면 어떤 것이 1개 나왔는지 알 수 있을 것이라고 생각했다.

Approach

문제가 constant extra space로 제한을 두고 있으므로 숫자의 범위가 중요해졌다.
다행히 숫자가 $-3 * 104 \leq nums[i] \leq 3 * 104$로 그리 많지는 않다.
0까지 포함하여 총 개수는 60001개로 배열로 충분히 구현할 수 있다.

int arr[60001];

그리고 원래 C표준 스펙이라면 전역변수는 자동으로 0으로 초기화되는게 맞는데, leetcode는 그렇지 않기때문에 따로 초기화를 진행해준다.

for (int i=0;i<60001;i++){
        arr[i]=0;
    }

이때 배열에 담을 숫자는 0부터 30000까지는 동일한 인덱스로 매칭시켜주면 되고, -1부터 -30000까지는 이후 배열인덱스인 30001부터 60001까지로 매칭시켜준다.

for (int i=0;i<numsSize;i++){
        if (nums[i]<0){
            arr[30000-nums[i]]++;
        }
        else{
            arr[nums[i]]++;
        }
    }

이제 한 번 nums 배열을 돌고나면 우리가 선언한 배열에 숫자들의 개수가 기록되었을 것이다. 그 중에 1로 기록되어있는 인덱스를 찾기만 하면 된다.
주의할 점은 30001부터는 다시 원래 숫자로 되돌려줘야 한다는 것이다.

int res;
    for (int i=0;i<60001;i++){
        if (arr[i]==1){
            if (i>30000){
                res=(i-30000)*(-1);
            }
            else{
                res=i;
            }
            break;
        }
    }

Solution

int arr[60001];

int singleNumber(int* nums, int numsSize){
    for (int i=0;i<60001;i++){
        arr[i]=0;
    }

    for (int i=0;i<numsSize;i++){
        if (nums[i]<0){
            arr[30000-nums[i]]++;
        }
        else{
            arr[nums[i]]++;
        }
    }

    int res;
    for (int i=0;i<60001;i++){
        if (arr[i]==1){
            if (i>30000){
                res=(i-30000)*(-1);
            }
            else{
                res=i;
            }
            break;
        }
    }
    return res;
}

Complexity

• Time Complexity : 배열 전체를 쭉 도는 반복문만 3개 있으므로 $O(n)$
• Space Complexity : 최대 숫자 범위만큼 존재한다. $O(n)$

교수님 풀이 1

보통 배열의 크기는 주어지는데, 배열 각각의 요소의 범위까지 주어지는 경우는 많이 없다고 한다. 그러므로 문제가 배열 원소를 인덱스로 쓰는 솔루션을 생각해보라는 힌트를 주는 것이라고 한다.
아이디어는 동일한데 교수님은 음수가 0~2999에 할당되도록 OFFSET을 설정하셨다.

그러나 이 풀이는 일반적으로 사용할 수 없다고한다. 배열 각각 요소의 범위가 굉장히 작게 설정 되었기 때문이다.

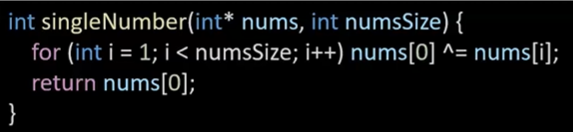
교수님 풀이 2

XOR을 사용하면 손쉽게 풀린다. XOR은 0이 아닌 숫자가 서로 같을 때에만 0을 반환하고 이 외의 경우에는 1을 반한하는 연산이다.
그리고 XOR은 결합법칙, 교환법칙이 모두 성립하므로 배열에 있는 모든 숫자를 대상으로 XOR연산을 수행하면 두 개 존재하는 숫자는 각각 모두 0을 반환할 것이고 한 개 있는 숫자만 그대로 남아 있을 것이다.

지적 및 질문 환영합니다.