[알고리즘] bit 연산 ①

양현지·2023년 12월 18일

알고리즘

목록 보기

20/27

1. Bitwise Operation?

데이터의 연산(산술연산, 논리 연산등) 수행 시 대부분의 경우 수치 및 논리적 조건을 다룰 때 bit 단위가 아닌 변수가 나타내는 데이터의 단위로 연산이 수행된다.

그러나, ip나 서브넷 마스크를 다루거나, 플래그 설정 및 해제 등의 경우에서는 비트 단위의 연산이 요구된다.

이러한 연산을 수행하기 위한 연산자를 bitwise operator(비트 연산자)라 한다.

2. Bitwise Operator

: 비트 연산을 위해 사용되는 연산자는 다음과 같다.

1) shift operators

① left shift ( << )

x << y

x의 모든 비트를 왼쪽으로 y만큼 이동

// x : 0011
int x=3;
// y : 0110 = 6
int y= (x<<1);
// z : 1100 = 12
int z= (x<<2);

<<1의 경우 x2배, <<2의 경우 x4배가 된 것을 확인할 수 있다.

② right shift ( >> )

x >> y

x의 모든 비트를 오른쪽으로 y만큼 이동

// x : 1100
int x=12;
// y : 0110 = 6
int y= (x>>1);
// z : 0011 = 3
int z= (x>>2);

>>1의 경우 x(1/2)배, >>2의 경우 x(1/4)배가 된 것을 확인할 수 있다.

2) logical operators

① Bitwise NOT (~)
: 변수 단위의 NOT 연산자는 "!" 인반면 비트 단위의 NOT 연산자는 "~"이다.

~(X)

X의 모든 비트를 반전(0->1, 1->0)

② Bitwise AND (&)
: 변수 단위의 AND 연산자는 "&&" 인반면 비트 단위의 AND 연산자는 "&"이다.

X&Y

X와 Y의 모든 비트를 AND 연산한 결과

③ Bitwise OR (|)
: 변수 단위의 OR 연산자는 "||" 인반면 비트 단위의 OR 연산자는 "|"이다.

X|Y

X와 Y의 모든 비트를 OR 연산한 결과

④ Bitwise XOR (^)
: 변수 단위의 XOR 연산자는 "!=" 인반면 비트 단위의 XOR 연산자는 "^"이다.

X^Y

X와 Y의 모든 비트를 XOR 연산한 결과

3. Implementation

bit 연산자를 활용해 문제 해결에 적용해보도록 한다.

1) 문제 출처

프로그래머스 : 2개 이하로 다른 비트 lv2.

2) 문제 개요

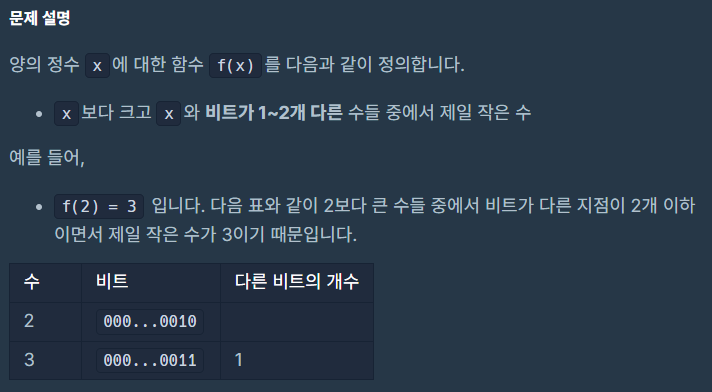
입력에 대해 조건(ⓐ입력값보다 크고, ⓑ비트가 1개 or 2개가 다른 수)을 만족하는 수 중 최소값을 구할 것

3) 제한 사항

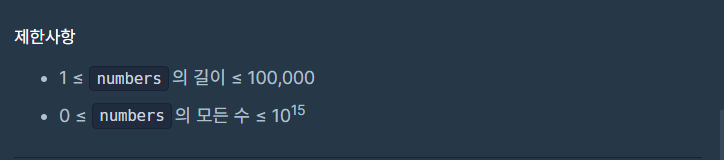
제한 사항을 토대로 numbers의 원소가 int범위를 넘어서 long long 으로 처리되어야함을 알 수 있다.

4) 입출력 예시

5) 알고리즘

대부분의 시스템에서 'long long' 데이터타입은 64bit이다.

ⓐ 짝수의 경우

+1이 조건을 만족하는 최소값

6 (0110)
→ 0111

ⓑ 홀수의 경우

최하위 비트부터 '0'이 등장하는 위치에서 '0'->'1'로 변경
그 다음 '1'이 등장하는 위치에서 '1'->'0' 변경

11 (1011)
→ 1'1'11
→ 11'0'1 (13)

7 (0111)
→ '1'111
→ 1'0'11 (11)

비트 연산자를 활용해 위 알고리즘을 구현하도록 한다.

 		if (no % 2 == 0)
        {
            answer.push_back(no + 1);
            continue;
        }
        else
        {
            // 뒤에서부터 처음으로 '0'인 곳->'1' (npos)
            // '1'이 나온 다음 위치에서부터 처음으로 '1'인 숫자 -> '0' (xpos)
            
            int npos = 0;
            while (npos <= 63)
            {
                //1LL = 1 (long long) = 0000...0001 
                // no의 npos 위치가 0이라면
                if ((no & (1LL << npos)) == 0)
                    break;
                npos++;
            }
            int xpos = npos-1;
            bool isval = false;
            while (xpos >= 0)
            {
                if ((no & (1LL << xpos)) != 0)
                {
                    isval = true;
                    break;
                }
                xpos--;
            }
            no += pow(2, npos);
            if(isval)
				no -= pow(2, xpos);
            answer.push_back(no);
        }

위 코드 중 비트 연산자가 사용된 부분을 자세히 살펴보고자 한다.

ⓐ 홀수인 경우 - npos 구하기
: 뒤에서부터 최초로 '0'이 아닌 비트의 위치 탐색

            while (npos <= 63)
            {
                if ((no & (1LL << npos)) == 0)
                    break;
                npos++;
            }

1LL = 1의 long long 표현 ( 00....0001)
1LL << npos : 1을 좌측으로 npos 이동, 즉 npos 위치에 비트값이 1인 상태
no & (1LL<<npos) : no가 npos 위치에 '1'인지 확인
1이라면 → 결과값은 0이 아니다.
0이라면 -> 결과값은 0이다. (찾고자 하는 npos의 위치)

ⓑ 홀수인 경우 - xpos 구하기
: npos로부터 최초로 '1'인 비트의 위치 탐색 (없다면 isval(false))

 		while (xpos >= 0)
            {
                if ((no & (1LL << xpos)) != 0)
                {
                    isval = true;
                    break;
                }
                xpos--;
            }

1LL = 1의 long long 표현 ( 00....0001)
1LL << xpos : 1을 좌측으로 xpos 이동, 즉 xpos 위치에 비트값이 1인 상태
no & (1LL<<xpos) : no가 xpos 위치에 '1'인지 확인
1이라면 → 결과값은 0이 아니다. (=1이다. 찾고자 하는 xpos의 위치)
0이라면 -> 결과값은 0이다.