[알고리즘] DFS/BFS 활용 ①

양현지·2023년 12월 7일

알고리즘

목록 보기

19/27

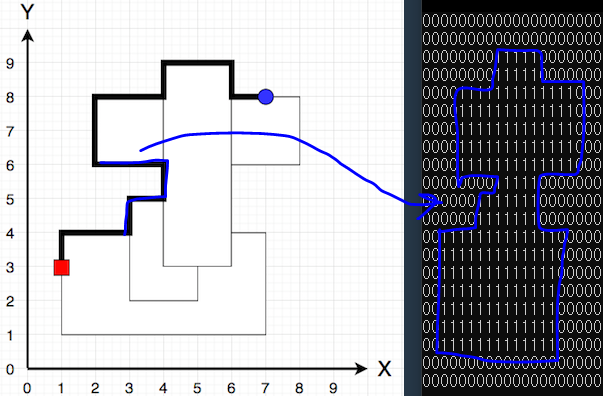
1. 문제 개요

문제 출처 : 프로그래머스 아이템 줍기 lv3

1) 문제 정의

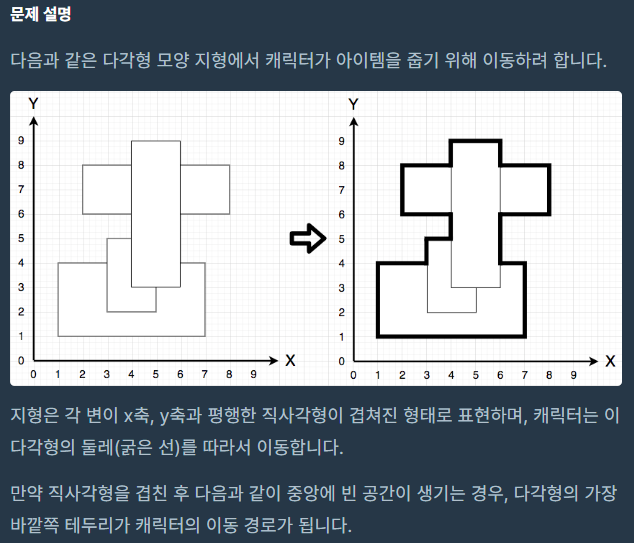
사각형의 외각 경로를 따라 (characterX,characterY) -> (itemX,itemY) 최소 이동 경로를 구할 것

2) 제한 사항

※ 존재하지 않는 경우

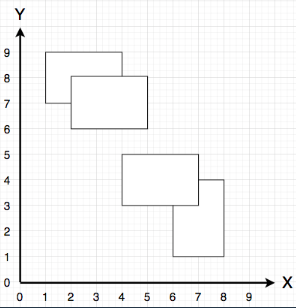
지형이 2개 이상이거나,

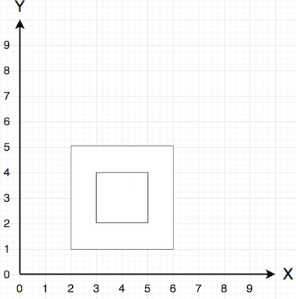
포함관계의 직사각형

3) 입출력 형식

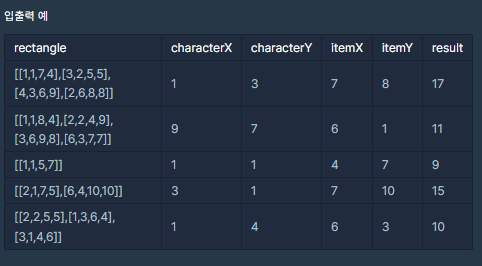
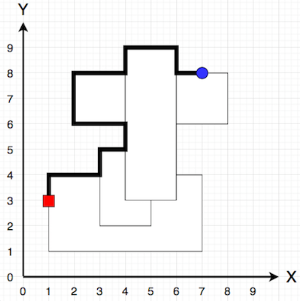
위 예시 중 1번의 경우는 다음 그림과 같이 설명된다.

이에 따라 이 문제는 (1)이동 가능 영역(사각형의 최외각)을 정의하고, (2)이동 가능영역을 따라 최소 이동 거리를 계산 하는 알고리즘을 구현해야한다.

2. Solution I.

1) 알고리즘

① 사각형이 내부 채우기

좌표 그대로 1로 채운 경우

-> 좌측의 사각형 모서리가 표시되지 않음

따라서 좌표x2배로 지도를 재구성하여 사각형 내부를 채우도록 한다.

// 1.1 사각형 채우기
    for (int i = 0;i < rectangle.size();i++)
    {
        int a, b, c, d;
        a = rectangle[i][0];
        b = rectangle[i][1];
        c = rectangle[i][2];
        d = rectangle[i][3];
        // (b,a) -> (d,c)
        for (int m = 2 * b;m <= 2 * d;m++)
            for (int n = 2 * a;n <= 2 * c;n++)
                mp[m][n] = 1;
    }

좌표x2배만큼 1로 채운 경우

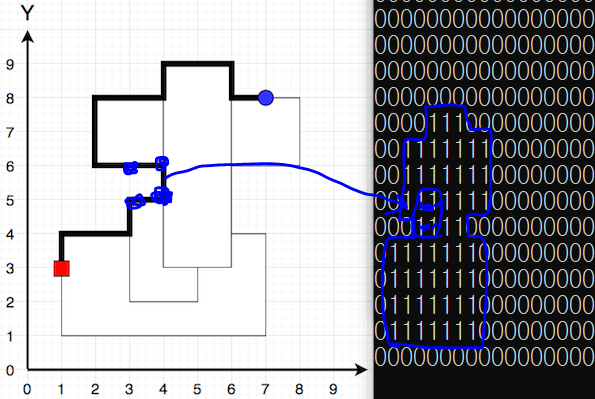
② 사각형 외각만 남기기 (이동 가능 영역)
이제 사각형의 테두리 영역을 제외하고 0으로 변환하여 사각형 비우기를 구현한다.

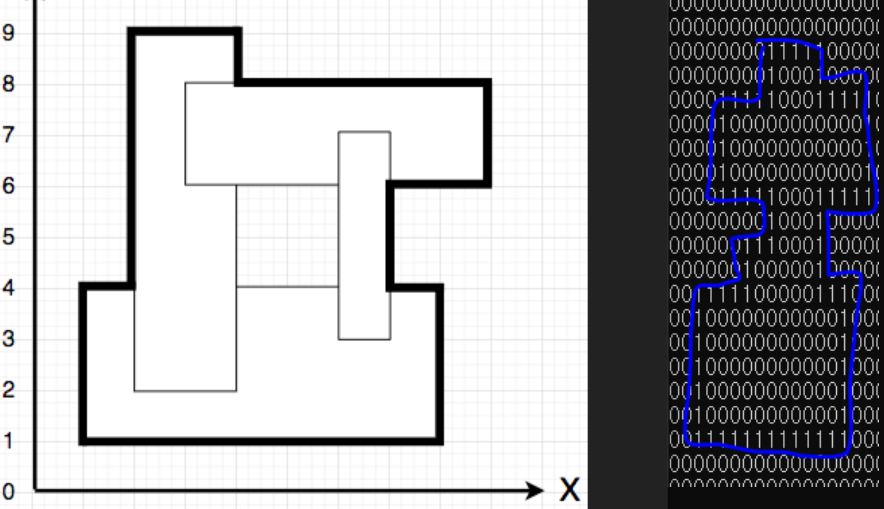
 // 1.2 사각형 비우기
    for (int i = 0;i < rectangle.size();i++)
    {
        int a, b, c, d;
        a = rectangle[i][0];
        b = rectangle[i][1];
        c = rectangle[i][2];
        d = rectangle[i][3];
        // (b,a) -> (d,c)
        for (int m = 2 * b + 1;m <= 2 * d - 1;m++)
            for (int n = 2 * a + 1;n <= 2 * c - 1;n++)
                mp[m][n] = 0;
    }

③ 이동 가능 영역(1) 내에서 DFS

// 2. dfs 탐색 : (a,b) -> (x,y)
int mp[101][101] = { 0, };
int answer = 0;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool v[101][101] = { false, };

void DFS(int a, int b, int x, int y, int cnt)
{
    if (a == x || b == y)
    {
        answer = cnt;
        return;
    }
    for (int i = 0;i < 4;i++)
    {
        if (a + dx[i] <= 0 || a + dx[i] >= 101 || b + dy[i] <= 0 || b + dy[i] >= 101)
            continue;
        if (mp[a + dx[i]][b + dy[i]] == 1 && v[a + dx[i]][b + dy[i]] == false)
        {
            v[a + dx[i]][b + dy[i]] = true;
            DFS(a + dx[i], b + dy[i], x, y, ++cnt);
            v[a + dx[i]][b + dy[i]] = false;
        }
    }

}

④ 전체 코드

#include <string>
#include <vector>
#include <iostream>

using namespace std;

// 1. 이동가능영역(사각형채우기->비우기)
// 2. DFS
int mp[101][101] = { 0, };
int answer = 987654321;
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
bool v[101][101] = { false, };

void DFS(int a, int b, int x, int y, int cnt)
{
    if (a == x && b == y)
    {
        answer = min(answer,cnt);
        return;
    }
    for (int i = 0;i < 4;i++)
    {
        if (a + dx[i] <= 0 || a + dx[i] >= 101 || b + dy[i] <= 0 || b + dy[i] >= 101)
            continue;
        if (mp[a + dx[i]][b + dy[i]] == 1 && v[a + dx[i]][b + dy[i]] == false)
        {
            v[a + dx[i]][b + dy[i]] = true;
            DFS(a + dx[i], b + dy[i], x, y, cnt+1);
            v[a + dx[i]][b + dy[i]] = false;
        }
    }

}

int solution(vector<vector<int>> rectangle, int characterX, int characterY, int itemX, int itemY)
{
    // 1.1 사각형 채우기
    for (int i = 0;i < rectangle.size();i++)
    {
        int a, b, c, d;
        a = rectangle[i][0];
        b = rectangle[i][1];
        c = rectangle[i][2];
        d = rectangle[i][3];
        // (b,a) -> (d,c)
        for (int m = 2 * b;m <= 2 * d;m++)
            for (int n = 2 * a;n <= 2 * c;n++)
                mp[m][n] = 1;
    }

    // 1.2 사각형 비우기
    for (int i = 0;i < rectangle.size();i++)
    {
        int a, b, c, d;
        a = rectangle[i][0];
        b = rectangle[i][1];
        c = rectangle[i][2];
        d = rectangle[i][3];
        // (b,a) -> (d,c)
        for (int m = 2 * b + 1;m <= 2 * d - 1;m++)
            for (int n = 2 * a + 1;n <= 2 * c - 1;n++)
                mp[m][n] = 0;
    }


    // 2. DFS
    v[characterY * 2][characterX * 2] = true;
    DFS(characterY * 2, characterX * 2, itemY * 2, itemX * 2, 0);


    return answer/2;
}