[알고리즘] DP 기본 ②

※ 문제 출처 : 소프티어 징검다리 lv3.

1. 문제 개요

1) 문제 설명

2) 제약 조건

3) 입출력 형식

2. Solution I.

1) DP를 활용한 풀이 ①

dp[i] : i번째 돌을 밟을 때를 마지막으로 하는 연속된 돌의 최대 길이
dp 배열의 최대값을 찾으면 그 값이 철수가 밟을 수 있는 돌의 최대 개수이다.

#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 점점 높은 돌을 밟으면서 지나감

int main(int argc, char** argv)
{
    int N;
    cin >> N;

    vector<int> s(N);
    // dp 배열 초기화 (1)
    vector<int> dp(N, 1);
	
    // 연속된 돌의 높이 입력
    for (int i = 0; i < N; ++i) 
    {
        cin >> s[i];
    }

	// i번째돌을 이전의 돌과 비교
    // -> 더 높다면, i번째 돌을 추가로 연속하여 밟음
    // -> 더 낮거나 같다면, i번째 돌을 새로 밟아야함 (1)
    for (int i = 1; i < N; ++i) 
    {
        if (s[i] > s[i - 1]) 
        {
            dp[i] = dp[i - 1] + 1;
        }
    }

    int max_length = *max_element(dp.begin(), dp.end());
    cout << max_length << endl;

    return 0;
}

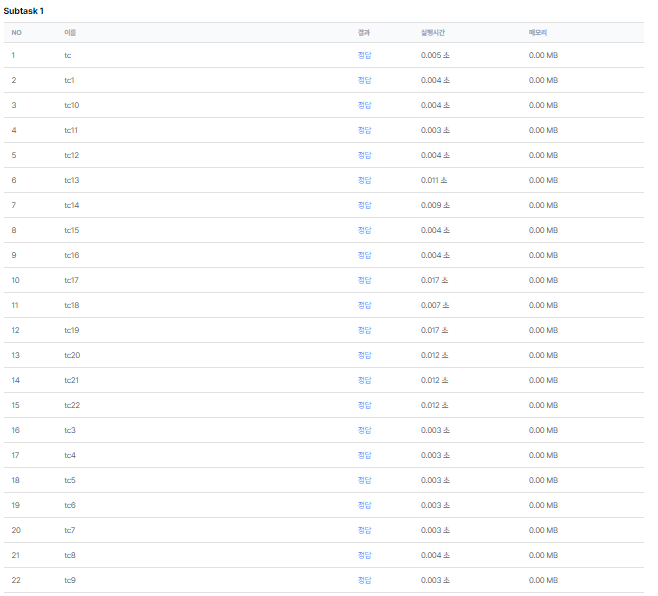
2) 실행 결과

위 코드 실행 및 제출 시 다음과 같은 결과를 확인할 수 있다.
시간 초과 혹은 메모리의 이슈는 아니며, 놓친 부분을 찾아보도록 한다.

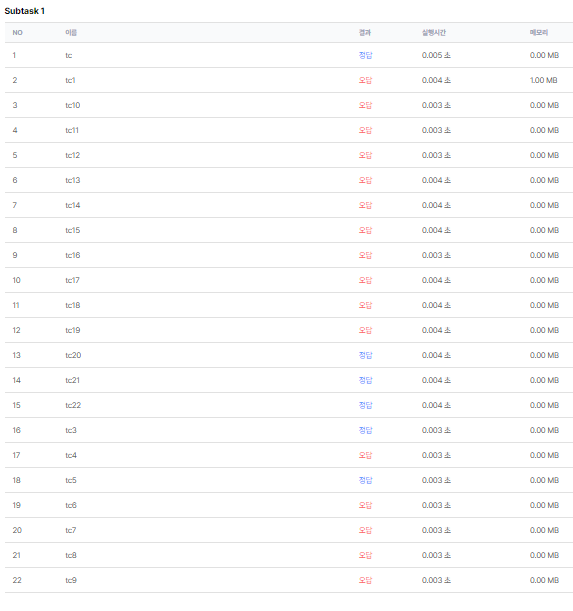
2. Solution II.

1) 반례 찾기

5
2 7 4 6 3

위의 경우 2->4->6을 차례로 밟으면 문제의 조건을 만족하므로, 출력값은 3이 출력되어야 한다. 그러나, Solution I.의 풀이에 따르면 출력값은 2가 나온다.

이는 문제의 풀이가 연속된 돌이 오름차순인 경우만을 인정하기 때문이다.

2) DP를 활용한 풀이 ②

#include<iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 점점 높은 돌을 밟으면서 지나감

int main(int argc, char** argv)
{
    int N;
    cin >> N;

    vector<long long> s(N);
    vector<int> dp(N, 1);

    for (int i = 0; i < N; ++i) {
        cin >> s[i];
    }

    for (int i = 1; i < N; ++i) 
    {
        for (int j = 0; j < i; ++j) 
        {
            if (s[i] > s[j]) 
            {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
    }

    int max_length = *max_element(dp.begin(), dp.end());
    cout << max_length << endl;

    return 0;
}