💡코드 없는 알고리즘과 데이터 구조을 바탕으로 작성된 글입니다.
정렬 알고리즘
정렬을 하는 이유?
데이터를 정렬하면 알고리즘이 중복 데이터를 빠르게 식별하거나 필요한 데이터를 매우 빠르게 찾을 수 있다.
버블 정렬
시간 복잡도 : O(n^2)
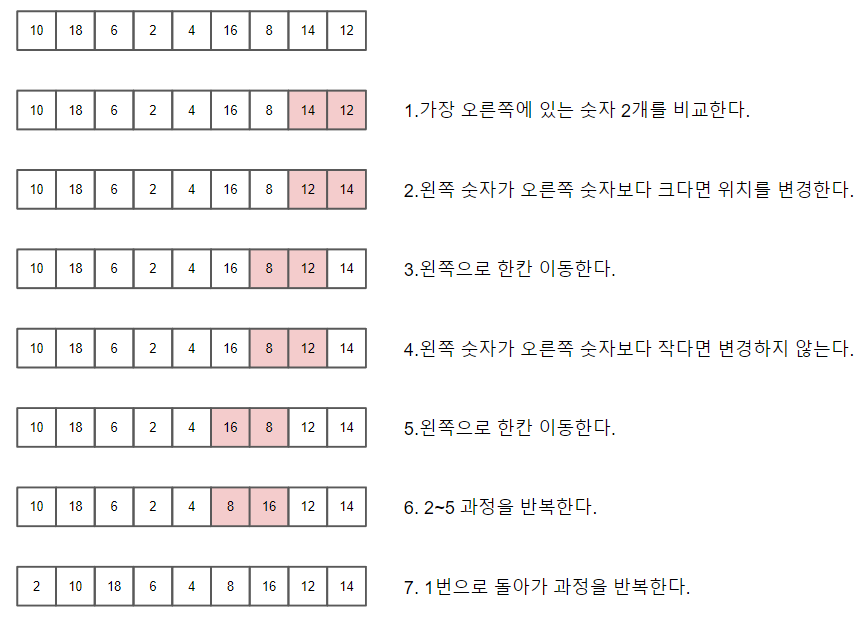
단순하지만, 느리고 비효율적이다.
선택 알고리즘
시간 복잡도 : O(n^2)
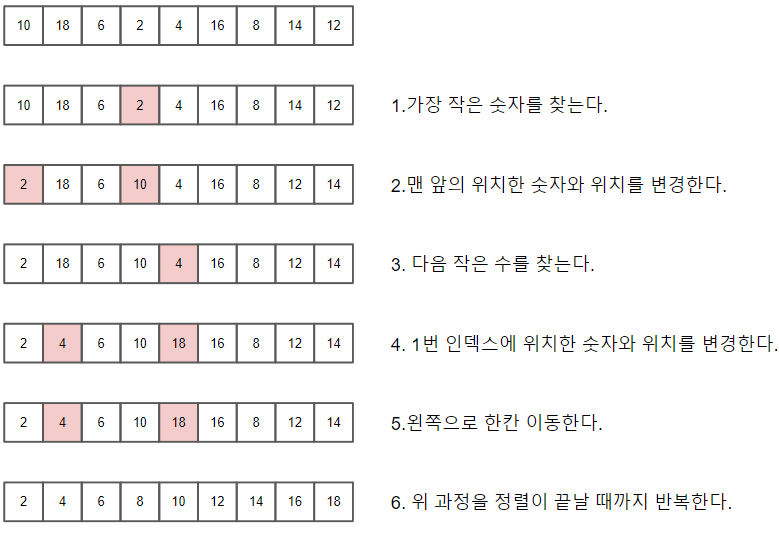
선택 정렬은 선형 탐색을 응용한 알고리즘으로 중첩 반복문을 사용하여 구현한다. 또한, 배열에서 가장 작은 수를 찾기 위해 선형 탐색을 하기 때문에 요소의 개수가 늘어날수록 실행 속도는 느려진다.
버블 정렬과 같은 시간 복잡도를 가지지만 버블 정렬보다는 조금 더 나은 성능을 제공한다.
삽입 정렬
시간 복잡도 : 최선 - O(n), 평균 - O(n^2), 최악 - O(n^2)

널리 사용되는 훌륭한 정렬 알고리즘이며 선택 정렬보다 더 효율적인 정렬 알고리즘이다.
셸 정렬
시간 복잡도 : 최선 - O(n), 평균 - O(n^1.5), 최악 - O(n^2)
삽입 정렬을 더 효율적으로 실행하는 알고리즘으로 다음과 같이 동작한다.
- 요소를 몇 개 단위로 묶은 후 단위마다 삽입 정렬을 실행한다.
- 이후 단위 요소 수를 줄여 묶은 후 삽입 정렬을 실행한다.
- 단위 요소 수가 1이 될 때까지 실행하면 정렬이 완료된다.

병합 정렬
시간 복잡도 : O(nlogn)
데이터를 반으로 나누어 정렬을 수행하는 알고리즘으로 분할 정복이라 한다.

재귀 함수를 사용하여 구현하며, 데이터를 계속 나누기 때문에 재귀 횟수에 따라 시간 복잡도가 달라지나 일반적으로 O(nlogn)로 나타난다.
퀵 정렬
시간 복잡도 : O(nlogn)
퀵 정렬도 병합 정렬처럼 분할 정복 방식을 사용한다.
중요한 것은 퀵 정렬에서는 피벗(Pivot)의 개념을 사용하는데 피벗은 이동의 기준이 된다.
일반적으로 피벗은 가장 맨 왼쪽에 있는 요소나 맨 오른쪽에 있는 요소를 선택해서 사용한다.


힙 정렬
시간 복잡도 : O(nlogn)
최대 힙
- 최대 값을 찾는다.
- 최대 값을 갖는 노드를 바로 위 부모 노드의 값과 비교하고, 최대 값이 클 경우 부모 노드와 위치를 변경한다.
- 그 다음 최대 값을 찾아 위 과정을 반복한다.
최소 힙
최대 힙과 반대로 자식 노드와 부모 노드의 값을 비교해 더 작은 쪽을 루트 노트에 가깝도록 위치시키면 된다.
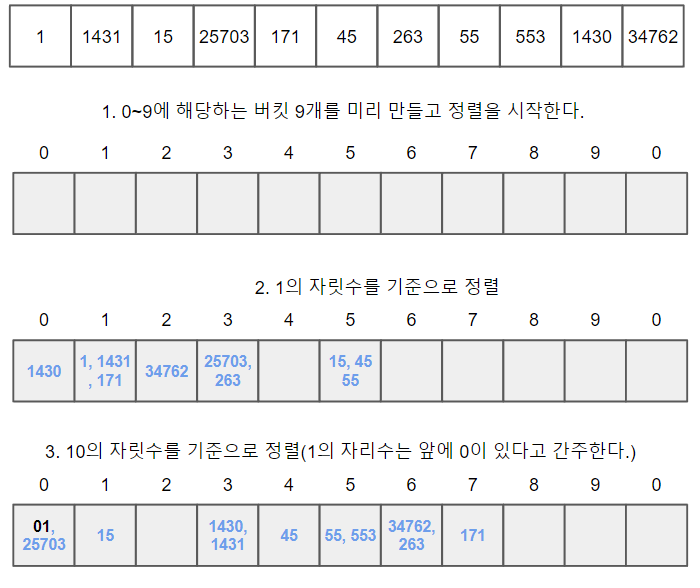
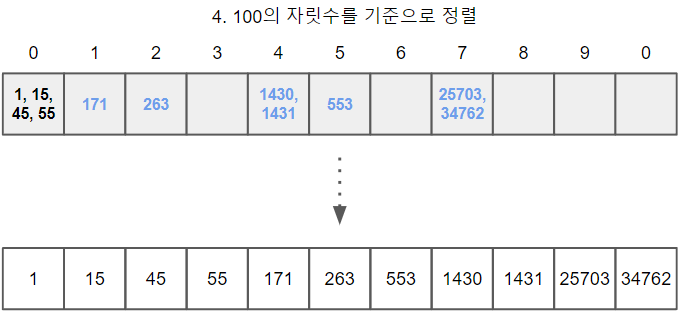
버킷 정렬
시간 복잡도 : 평균 - O(n+n^2/m+m), 최악 - O(n^2) (m은 버킷 수)
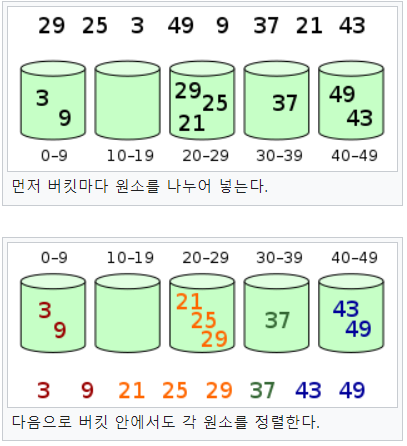
이미지 출처 : 위키피디아-버킷정렬
버킷 정렬은 요소들을 어떤 기준이 있는 버킷에 나눠 넣은 후 다음 과정으로 정렬을 수행한다.
이때의 기준은 보통 10진수의 자리수이다.
- 어떤 순서가 있는 버킷으로 사용할 기억공간(배열이나 리스트)를 준비한다.
- 버킷을 만들 때의 기준에 따라 요소를 분류하여 넣는다.
- 버킷별로 요소를 정렬한다.
- 버킷 안에서 정렬한 요소를 버킷의 순서에 따라 나열해서 정렬을 완료한다.
기수 정렬
시간 복잡도 : 최악 - O(mn) (m은 요소의 자리수)
특정 기준이 정해져 있는 버킷 정렬과 달리 기수 정렬의 기준은 바로 요솟값의 특정 자릿수끼리 비교해서 정렬한다는 것이다.