💡코드 없는 알고리즘과 데이터 구조을 바탕으로 작성된 글입니다.

선형 및 이진 탐색

탐색은 알고리즘에서 중요한 역할을 담당하며, 탐색 알고리즘의 가장 기본적인 방법은 선형과 이진 탐색이다.

💡여기서 잊지 말아야 할 것
알고리즘은 다양한 데이터 구조에 대해 가능한 빠른 검색을 지향하도록 설계되어 있다.

선형 탐색

선형성

선형성은 말 그대로 그래프에서 직선으로 나타낼 수 있음을 말한다.

여기서 중요한 점은 그래프에 있는 직선을 축 2개의 숫자 쌍으로 나타낸다는 것이다.

선형 탐색의 원리

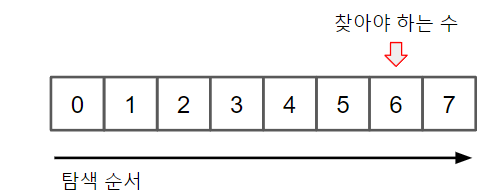
0부터 7까지의 인덱스를 가지는 배열이 있다고 가정하였을 때, 인덱스 6에 해당하는 값을 찾아야 한다.

0, 1, 2, 3, 4, 5번의 인덱스를 거쳐 6번에 도달하면 탐색은 종료한다. 얼핏 보면 매우 간단하고 빠른 것 처럼 느껴지지만 배열의 길이가 길면 길어질수록 탐색 속도는 증가한다.

선형 탐색의 문제점

선형 알고리즘은 원하는 값을 얻기 위해 배열의 모든 요소를 살펴봐야 하며 그로 인해 속도가 매우 느리다. 시간 복잡도로는 O(n)에 해당하며 비효율적이라는 단점을 보완하기 위해 로그형 탐색 기술인 이진 탐색이 존재한다.

이진 탐색

로그

이진 탐색을 알기 전에 이진 탐색의 기반이 되는 로그를 알아야 한다. 로그를 알기 전에는 지수를 먼저 알아야 한다!

지수

지수는 거듭제곱 을 나타내는 수를 말한다.

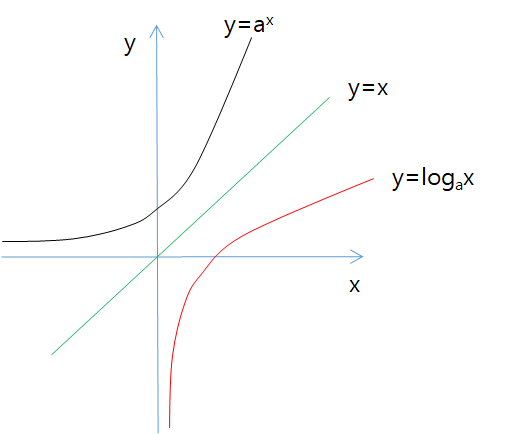
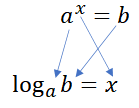
지수 함수의 역함수가 로그함수이며, 지수와 로그는 역의 관계이다. 이 점을 꼭 기억하자!

이진 탐색의 원리

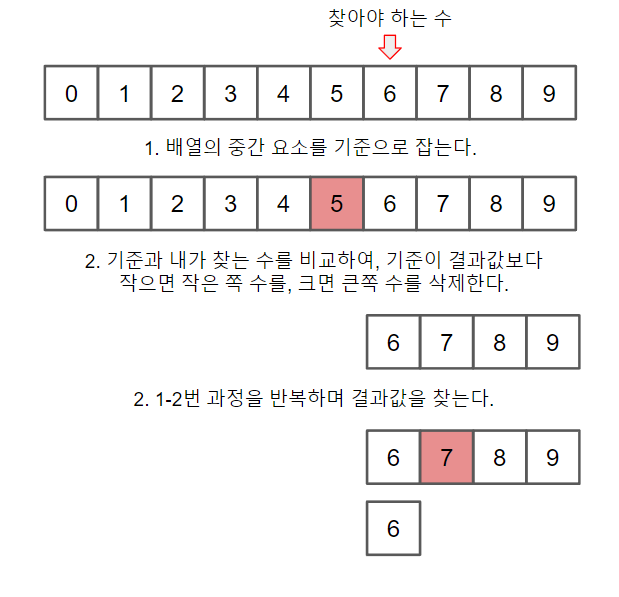
이진 탐색은 배열의 크기를 반으로 쪼개가며 결과값을 찾는다. 이는 선형 탐색보다 처리 속도가 빠르다.

그런데 이런 이진 탐색이 어째서 로그와 관련이 있는걸까? 이진 탐색은 중간 요소와 결과값을 비교할 때마다 탐색 범위가 반으로 줄어든다.

정렬된 데이터 수를 n, 비교 횟수를 m이라고 하면 다음 식이 성립한다.

n X(1/2)^m = 1
n = 2^m
m = log2n (2는 아랫수)

이에 따라 이진 탐색의 시간복잡도는 O(logn)이다.

이진 탐색을 사용할 때 주의할 점

이진 탐색의 원리를 살펴보면 배열의 값을 원하는 값과 비교해가며 반을 쪼개간다. 이는 배열이 정렬되어 있지 않은 상태에서는 올바르게 동작하지 않는다는 것을 뜻한다.